Закон Джоуля – Ленца. Работа и мощность тока.
Похожие статьи вашей тематики
Проводник нагревается, если по нему протекает электрический ток. Джоуль и Ленц установили, что количество выделившегося тепла
Q = I  Rt, (12-26) Rt, (12-26)
где I - ток, R - сопротивление, t - время протекания тока. Легко доказать, что
Q = I  Rt = UIt = U 2 t/R = qU, (12-27) Rt = UIt = U 2 t/R = qU, (12-27)
где q = It - электрический заряд.
Если ток изменяется со временем (т. е. в случае непостоянного тока), то
Q =  = =  ,(12-28) ,(12-28)
где i - мгновенное значение тока.
Нагревание проводника происходит за счет работы, совершаемой силами электрического поля над носителями заряда. Эта работа
A=qU=UIt=I  Rt = U Rt = U  t / R. (12-29) t / R. (12-29)
Работа А, энергия W, количество тепла Q в СИ измеряются в Дж.
Так как мощность характеризует работу, совершаемую в единицу времени, т.е. Р =  , то , то
P=UI=I  R=U R=U  /R. (12-30) /R. (12-30)
Мощность в СИ измеряется в ваттах: 1 Вт = 1 Дж / 1 с; откуда 1 Дж = 1 Втс;
3600 Дж = 1Вт час, 3,6 •10  Дж = 1 кВт час. Дж = 1 кВт час.
Формулы (12-29) и (12-30) позволяют рассчитать полезную работу и полезную мощность. Затраченная работа и мощность определяется по формулам
A  = q = q 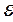 = = 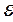 It = I It = I  (R + r)t = (R + r)t =  t. (12-31) t. (12-31)
P 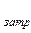 = =  = =  I = I I = I  (R + r) = (R + r) =  . (12-32) . (12-32)
Отношение полезной работы (мощности) к затраченной характеризует КПД источника
 = =  = =  = =  . (12-33) . (12-33)
Из (12-33) следует, что при R®0,h®0; R®¥,h®1. Но при R   ток I ток I  0 и поэтому А 0 и поэтому А  О и Р О и Р  0. 0.
Определим величину R, при котором выделится максимальная мощность. Легко показать, что это наступает при R = r, тогда
PMAКС=I  R = R =  = =  , (12-34) , (12-34)
КПД в этом случае будет 50%.
Согласно закону Джоуля - Ленца в элементарном цилиндрическом объеме dV с площадью поперечного сечения dS и длиной dl за время dt выделится тепло
dQ = I  Rdt = (jdS) Rdt = (jdS)  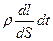 = =  j j  dldSdt = dldSdt =  j j  dVdt. dVdt.
Разделив на dV и dt, найдем количество тепла, выделяющееся в единицу времени в единице объема
Q  = = 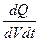 = =  j j  . (12-35) . (12-35)
здесь Q  -называется удельной тепловой мощностью тока, которая в СИ измеряется в Вт/м3. -называется удельной тепловой мощностью тока, которая в СИ измеряется в Вт/м3.
С учетом (12-16) из (12-3) следует, что
Q  = =  j j  = = 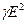 . (12-36) . (12-36)
Формулы (12-35) и (12-36) выражают закон Джоуля - Ленца в дифференциальной форме.
Правила Кирхгофа
В основе расчета электрических цепей лежат два правила Кирхгофа:
Первое правило: Алгебрическая сумма токов, сходящихся в узле равна нулю, т.е.
 . (12-37) . (12-37)
Току, текущему к узлу, приписывается один знак ("+" или "-"), а току, текущему от узла, - другой знак; таким образом, для направлений токов в узле электрической схемы, представленном на рис.12. 6, имеем  . .
Второе правило: В любом замкнутом контуре алгебраическая сумма напряжений на всех участках этого контура равна алгебраической сумме ЭДС, встречающихся в этом контуре, т.е.
 (12-38) (12-38)

При этом также следует придерживаться правила знаков: токи, текущие вдоль выбранного направления обхода контура считаются положительными, а идущие против направления обхода - отрицательными. Соответственно положительными считаются ЭДС тех источников, которые вызывают ток, совпадающий по направлению с обходом контура (рис.12.7), где обозначает направление обхода контура.
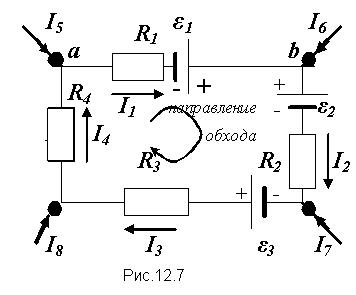
 Применим правила Кирхгофа для расчета электрической цепи, представленной на рис.12.7. Для этого нужно записать (m-1) уравнений для основании первого правила Кирхгофа и еще одно уравнение для единственного здесь замкнутого контура, используя второе правило Кирхгофа и принимая во внимание направления ЭДС, токов в ветвях и обхода контура: Применим правила Кирхгофа для расчета электрической цепи, представленной на рис.12.7. Для этого нужно записать (m-1) уравнений для основании первого правила Кирхгофа и еще одно уравнение для единственного здесь замкнутого контура, используя второе правило Кирхгофа и принимая во внимание направления ЭДС, токов в ветвях и обхода контура:
I 
I  I I 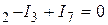
 . .
Лекция №13
Электрический ток в различных средах. Классическая теория электропроводности металлов. Термоэлектронная эмиссия. Электрический ток в вакууме. Электрический ток в газах. Виды газового разряда.
|