Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электромагнитная теория Максвелла.Содержание книги
Поиск на нашем сайте
В 60-х годах прошлого века (около 1860 г.) Максвелл, основываясь на идеях Фарадея, обобщил законы электростатики и электромагнетизма: теорему Гаусса - Остроградского для электростатического поля Теория Максвелла явилась величайшим вкладом в развитие классической физики. Она позволила с единой точки зрения понять широкий крут явлений, начиная от электростатического поля неподвижных зарядов и заканчивая электромагнитной природой света. Математическим выражением теории Максвелла служат четыре уравнения Максвелла. которые принято записывать в двух формах: интегральной и дифференциальной. Дифференциальные уравнения получаются из интегральных с помощью двух теорем векторного анализа - теоремы Гаусса и теоремы Стокса. Теорема Гаусса:
Теорема Стокса: здесь rot rot S - площадь, ограниченная контуром L. Уравнения Максвелла в интегральной форме выражают соотношения, справедливые для мысленно проведенных в электромагнитном поле неподвижных замкнутых контуров и поверхностей. Уравнения Максвелла в дифференциальной форме показывают как связаны между собой характеристики электромагнитного поля и плотности зарядов и токов в каждой точке этого поля.
1) Первое уравнение Максвелла Оно является обобщением закона электромагнитной индукции и в интегральной форме имеет следующий вид
и утверждает, что с переменным магнитным полем
Из сравнения (15-15) и (15-16) находим, что
Это и есть первое уравнение Максвелла в дифференциальной форме.
2) Ток смешения. Второе уравнение Максвелла Максвелл обобщил закон полного тока По теореме Гаусса - Остроградского поток электрического смешения сквозь замкнутую поверхность
Продифференцировав это выражение по времени, получим для неподвижной и недеформируемой поверхности S
Левая часть этой формулы имеет размерность тока, который, как известно, выражается через вектор плотности тока
Из сравнения (15-18) и (15-19) следует, что
Ток смещения
Из всех физических свойств, присущих действительному току (току проводимости), связанному с переносом зарядов, ток смешения обладает лишь одним: способностью создавать магнитное поле. При "протекании" тока смещения в вакууме или диэлектрике не выделяется тепло. Примером тока смещения может служить переменный ток через конденсатор. В общем случае токи проводимости и смещения не разделены в пространстве и можно говорить о полном токе, равном сумме токов проводимости и смещения: С учетом этого Максвелл обобщил закон полного тока, добавив в правую часть его ток смешения
Итак, второе уравнение Максвелла в интегральной форме имеет вид:
Из (15-13) следует, что
Из сравнения (15-24) и (15-25) находим, что
Это и есть второе уравнение Максвелла в дифференциальной форме. 3)Третье и четвертое уравнения Максвелла Максвелл обобщил теорему Гаусса - Остроградского для электростатического поля. Он предположил, что эта теорема справедлива для любого электрического поля, как стационарного, так и переменного. Соответственно, третье уравнение Максвелла в интегральной форме имеет вид:
или где Из (15-12) следует, что
Из сравнения (15-28) и (15-29) находим,что
Четвертое уравнение Максвелла в интегральной и дифференциальной формах имеет следующий вид:
4)Полная система уравнений Максвелла в дифференциальной форме
Эту систему уравнений необходимо дополнить материальными уравнениями, характеризующими электрические и магнитные свойства среды:
Итак, после открытия взаимосвязи между электрическими и магнитным полями стало ясно, что эти поля не существуют обособлено, независимо одно от другого. Нельзя создать переменное магнитное поле без того, чтобы одновременно в пространстве не возникло и электрическое поле. Отметим, что покоящийся в некоторой системе отсчета электрический заряд создает только электростатическое поле в этой системе отсчета, но он будет создавать магнитное поле в системах отсчета, относительно которых он движется. То же самое относится и к неподвижному магниту. Заметим также, что уравнения Максвелла инвариантны к преобразованиям Лоренца: причем для инерциальных систем отсчета К и К’ На основании изложенного можно сделать вывод, что электрические и магнитные поля являются проявлением единого поля, которое называют электромагнитным полем. Оно распространяется в виде электромагнитных волн. Переменный ток Установившиеся вынужденные электромагнитные колебания можно рассматривать как протекание в цепи, содержащей резистор, катушку индуктивности и конденсатор, переменного тока. Переменный ток можно считать квазистационарным, т. е. для него мгновенные значения силы тока во всех сечениях цепи практически одинаковы, так как их изменения происходят достаточно медленно, а электромагнитные возмущения распространяются по цепи со скоростью, равной скорости света. Для мгновенных значений квазистационарных токов выполняются закон Ома и вытекающие из него правила Кирхгофа. Рассмотрим последовательно процессы, происходящие в цепи, содержащей резистор, катушку индуктивности и кон-
содержащей резистор, катушку индуктивности и конденсатор, при приложении к ней переменного напряжения U=Umcoswt, (15-33) где Um — амплитуда напряжения. Переменный ток, текущий через резистор сопротивлением R (L®0, С®0) (рис.15.1, а). При выполнении условия квазистационарности ток через резистор определяется законом Ома: I=U/R=(Um/R)coswt=Imcoswt, где амплитуда силы тока lm=Um/R. Для наглядного изображения соотношений между переменными токами и напряжениями воспользуемся методом векторных диаграмм. На рис. 15.1, б дана векторная диаграмма амплитудных значений тока Im и напряжения Um на резисторе (сдвиг фаз между Im и Um равен нулю). Переменный ток, текущий через катушку индуктивностью L (R®0, C®0) (рис. 15.2, а). Если в цепи приложено переменное напряжение (15-33), то в ней потечет переменный ток, в результате чего возникнет э.д.с. самоиндукции ξs =-LdI/dt. Тогда закон Ома для рассматриваемого участка цепи имеет вид Umcoswt-LdI/dt=0, откуда LdI/dt=Umcosw. (15-34) Так как внешнее напряжение приложено к катушке индуктивности, то UL=LdI/dt (15-35) есть падение напряжения на катушке. Из уравнения (15-34) следует, что dI=(Um/L)coswt/dt, или после интегрирования, учитывая, что постоянная интегрирования равна
нулю (так как отсутствует постоянная составляющая тока), получим (15-36)
Величина RL= wL (15-37) называется реактивным индуктивным сопротивлением (или индуктивным сопротивлением). Из выражения (15-36) вытекает, что для постоянного тока (w=0) катушка индуктивности не имеет сопротивления. Подстановка значения Um=wLIm в выражение (15-34) с учетом (15-35) приводит к следующему значению падения напряжения на катушке индуктивности: UL=wLImcoswt. (15-38) Сравнение выражений (15-36) и (15-38) приводит к выводу, что падение напряжения UL опережает по фазе ток I, текущий через катушку, на p/2, что и показано на векторной диаграмме (рис. 15.2, б). Переменный ток, текущий через конденсатор емкостью С (R®0, L ®0 ) Если переменное напряжение приложено к конденсатору, то он все время перезаряжается, и в цепи потечет переменный ток. Так как все внешнее напряжение приложено к конденсатору, а сопротивлением подводящих проводов можно пренебречь, то
Q/C=UC=Umcoswt. Сила тока (15-38)
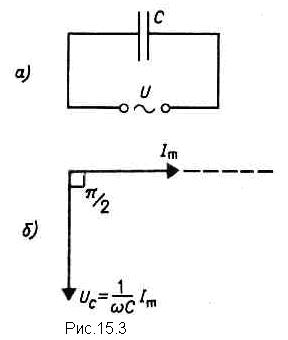
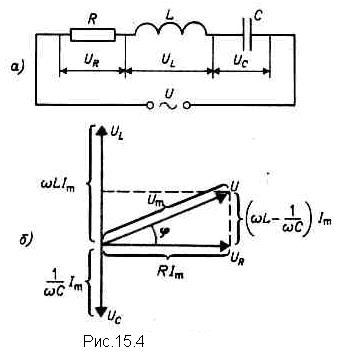
Величина RC=1/(wС) называется реактивным емкостным сопротивлением (или емкостным сопротивлением). Для постоянного тока (w=0) RC=¥, т. е. постоянный ток через конденсатор течь не может. Падение напряжения на конденсаторе UC=(1/wC)Imcoswt. (15-39) Сравнение выражений (15-38) и (15-39) приводит к выводу, что падение напряжения UC отстает по фазе от текущего через конденсатор тока I на p/2. Это показано на векторной диаграмме (рис. 15.3, б). Цепь переменного тока, содержащая последовательно включенные резистор, катушку индуктивности и конденсатор. На рис. 15.4,а представлена цепь, содержащая резистор сопротивлением R, катушку индуктивностью L и конденсатор емкостью С, на концы которой подается переменное напряжение. В цепи возникнет переменный ток, который вызовет на всех элементах цепи соответствующие падения напряжения UR, UL и UC. На рис. 15.4, б представлена векторная диаграмма амплитуд падений напряжений на резисторе (UR), катушке (UL) и конденсаторе (UC). Амплитуда Um приложенного напряжения должна быть равна векторной сумме амплитуд этих падений напряжений. Как видно из рис. 15.4, б, угол j определяет разность фаз между напряжением и силой тока. Из рисунка следует, что
Из прямоугольного треугольника получаем,
откуда амплитуда силы тока имеет значение
Таким образом, если напряжение в цепи изменяется по закону U=Um cosw t, то в цепи течет ток I = Imcos(wt-j), (15-42) где j и Im определяются соответственно формулами (15-41) и (15-42). Величина
называется полным сопротивлением цепи, а величина
— реактивным сопротивлением. Рассмотрим частный случай, когда в цепи отсутствует конденсатор. В данном случае падения напряжений UR и UL в сумме равны приложенному напряжению U. Векторная диаграмма для данного случая представлена на рис. 15.5, из которого следует, что
Отсутствие конденсатора в цепи означает С=¥, а не С=0.
Резонанс напряжений Если в цепи переменного тока, содержащей последовательно включенные конденсатор, катушку индуктивности и резистор (рис.15.4), wL= 1/(wС), (15-45) то угол сдвига фаз между током и напряжением обращается в нуль (j=0), т. е. изменения тока и напряжения происходят синфазно. Условию (15-45) удовлетворяет частота wрез=l/ÖLC. (15-46) В данном случае полное сопротивление цепи Z становится минимальным, равным активному сопротивлению R цепи, и ток в цепи определяется этим сопротивлением, принимая максимальные (возможные при данном Um) значения. При этом падение напряжения на активном сопротивлении равно внешнему напряжению, приложенному к цепи (UR=U), а падения напряжений на конденсаторе (UC) и катушке индуктивности (UL) одинаковы по амплитуде и противоположны по фазе. Это явление называется резонансом напряжений (последовательным резонансом), а частота (15-46) — резонансной частотой. Векторная диаграмма для резонанса напряжений приведена на рис.15.6. В случае резонанса напряжений (UL)реэ=(UC)рез, поэтому, подставив в эту формулу значения резонансной частоты и амплитуды напряжений на катушке индуктивности и конденсаторе, получим
где Q — добротность контура. Так как добротность обычных колебательных контуров больше единицы, то напряжение как на катушке индуктивности, так и на конденсаторе превышает напряжение, приложенное к цепи. Поэтому явление резонанса напряжений используется в технике для усиления колебания напряжения какой-либо определенной частоты. Например, в случае резонанса на конденсаторе можно получить напряжение с амплитудой QUm (Q в данном случае — добротность контура), которая может быть значительно больше Um). Это усиление напряжения возможно только для узкого интервала частот вблизи резонансной частоты контура, что позволяет выделить из многих сигналов одно колебание определенной частоты, т. е. на радиоприемнике настроиться на нужную длину волны. Явление резонанса напряжений необходимо учитывать при расчете изоляции электрических линий, содержащих конденсаторы и катушки индуктивности, так как иначе может наблюдаться их пробой. Резонанс токов. Рассмотрим цепь переменного тока, содержащую параллельно включенные конденсатор емкостью С и катушку индуктивностью L (рис.15.7). Для простоты допустим, что активное сопротивление обеих ветвей настолько мало, что им можно пренебречь. Если приложенное напряжение изменяется по закону U=Um coswt(см. (149.1)), то, согласно формуле (15-42), в ветви 1С2 течет ток I 1=Im1cos(wt-j1), амплитуда которого определяется из выражения (15-41) при условии R =0 и L=0:
Разность фаз токов в ветвях 1С2 и 1L2 равна j1-j2=p, т. е. токи в ветвях противоположны по фазе. Амплитуда силы тока во внешней (неразветвленной) цепи Im=│Im1,-Im2│=Um│wC-l/(wL)|. Если w=wрез=1/ÖLС, то Im1=Im2 и Im=0. Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно включенные конденсатор и катушку индуктивности, при приближении частоты w приложенного напряжения к резонансной частоте wрез называется резонансом токов (параллельным резонансом). В данном случае для резонансной частоты получили такое же значение, как и при резонансе напряжений.
Амплитуда силы тока Im оказалась равна нулю потому, что активным сопротивлением контура пренебрегли. Если учесть сопротивление R, то разность фаз j1-j2 не будет равна p, поэтому при резонансе токов амплитуда силы тока Im будет отлична от нуля, но примет наименьшее возможное значение. Таким образом, при резонансе токов во внешней цепи токи I 1 и I 2 компенсируются и сила тока I в подводящих проводах достигает минимального значения, обусловленного только током через резистор. При резонансе токов силы токов I1 и I2 могут значительно превышать силу тока I. Рассмотренный контур оказывает большое сопротивление переменному току с частотой, близкой к резонансной, поэтому это свойство резонанса токов используется в резонансных усилителях, позволяющих выделять одно определенное колебание из сигнала сложной формы. Кроме того, резонанс токов используется в индукционных печах, где нагревание металлов производится вихревыми токами. В них емкость конденсатора, включенного параллельно нагревательной катушке, подбирается так, чтобы при частоте генератора получился резонанс токов, в результате чего сила тока через нагревательную катушку будет гораздо больше, чем сила тока в подводящих проводах.
|
||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.68.161 (0.012 с.) |

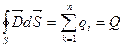 и для магнитного поля
и для магнитного поля  ; закон полного тока
; закон полного тока  ; закон электромагнитной индукции
; закон электромагнитной индукции  , и в результате разработал законченную теорию электромагнитного поля.
, и в результате разработал законченную теорию электромагнитного поля.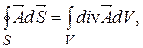 (15-12)
(15-12)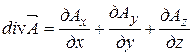
 - проекции вектора
- проекции вектора  на оси; V - объем, ограниченный поверхностью S.
на оси; V - объем, ограниченный поверхностью S. . (15-13)
. (15-13) , (15-14)
, (15-14)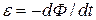 ,
, (15-15)
(15-15) неразрывно связано вихревое электрическое поле
неразрывно связано вихревое электрическое поле  , которое не зависит от того находятся в нем проводники или нет. Из (15-13) следует, что
, которое не зависит от того находятся в нем проводники или нет. Из (15-13) следует, что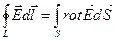 . (15-16)
. (15-16) (15-17)
(15-17)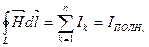 предположив, что переменное электрическое поле, также как и электрический ток, является источником магнитного поля. Для количественной характеристики "магнитного действия" переменного электрического поля Максвелл ввел понятие тока смещения.
предположив, что переменное электрическое поле, также как и электрический ток, является источником магнитного поля. Для количественной характеристики "магнитного действия" переменного электрического поля Максвелл ввел понятие тока смещения.
 (15-18)
(15-18)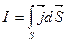 . (15-19)
. (15-19) имеет размерность плотности тока: А /м2. Максвелл предложил назвать
имеет размерность плотности тока: А /м2. Максвелл предложил назвать  . (15-20)
. (15-20) . (15-21)
. (15-21)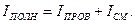 (15-22)
(15-22) . (15-23)
. (15-23) . (15-24)
. (15-24) . (15-25)
. (15-25)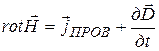 . (15-26)
. (15-26) . (15-27)
. (15-27) . (15-28)
. (15-28) - объемная плотность свободных зарядов, [
- объемная плотность свободных зарядов, [  ]= Кл / м3
]= Кл / м3
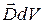 . (15-29)
. (15-29) . (15-30)
. (15-30)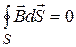 , (15-31)
, (15-31)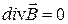 . (15-32)
. (15-32)
 .
.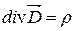 ,
,  .
. ,
,  ,
,  .
. выполняются следующие соотношения:
выполняются следующие соотношения: 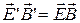 ,
, 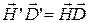 .
.

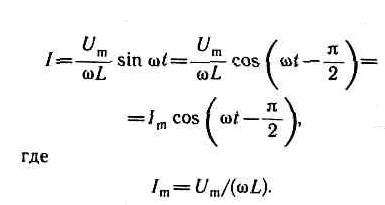

 (15-40)
(15-40)
 (15-41)
(15-41)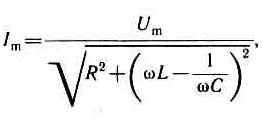 (15-43)
(15-43)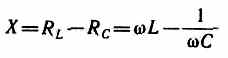
 (15-44)
(15-44)