работой сил давления f1 = p1S1 и f2 = p2S2, которые действуют на плоскости S1 и S2. Как видно из рис., часть элемента между сечениями 
и S2 остается неподвижной так, что изменение положения выделенного элемента сводится к перемещению отрезка, ограниченного сечениями S1 и в новое положение между плоскостями S2 и 
. Пусть плотность жидкости в сечении S1 равна r1, а в сечении S2 - r2. Масса отрезка между сечениями S1 и равна m1 = r1v1S1Dt, тогда как масса между S2 и равна m2 = r2v2S2Dt; поэтому кинетическая и потенциальная энергии массы m1 равны:
= 
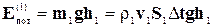. (4-8)
Аналогично для массы m2:
= 
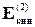(4-9)
где h1 и h2 - высоты центров тяжести первого и второго элементов относительно выбранного уровня отсчета потенциальной энергии.
На основании закона сохранения механической энергии можно записать:
= 
. (4-10)
Работа силы f2 взята со знаком минус потому, что направление силы и направление перемещения противоположны друг другу.
Подставляя в уравнение (4-10) значения кинетических и потенциальных энергий (4-8) и (4-9), получаем:
= 
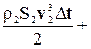
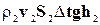
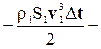
, (4-11)
откуда после сокращения на величину Dt (с учетом того, что v1S1 =v2 S2) следует:
= 
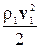
,(4-12)
или в общем виде:
+ р = const. (4-13)
Выражения (4-12) и (4-13) представляют различные формы записи уравнения Бернулли, имеющего ряд важных следствий практического характера.Если движение жидкости или газа происходит на постоянной высоте, то уравнение (4-13) упрощается: р = const, или 
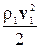
= . (4-14)
Из этого уравнения следует, что давление внутри трубки тока зависит от скорости: там, где скорость меньше, давление больше, при увеличении скорости потокадавление в нем уменьшается. Это утверждение называют принципом Бернулли.
Приложения уравнения Бернулли:подъемной силы крыла самолета, гидротрубина, гидротаран, водоструйный насос, аэрация почвы и т. д.
|
|
Лекция №5
Основные характеристики и закономерности колебаний. Гармонические колебания. Сложение гармонических колебаний. Сложение перпендикулярных колебаний. Дифференциальное уравнение колебаний. Свободные колебания. Затухающие колебания. Энергетические соотношения в колебательных процессах. Колебания математического и физического маятников
Гармонические колебания.
Колебаниями называются такие изменения какой - либо физической величины, когда эта величина через определенные промежутки времени принимает одни и те же значения. Любое колебание может быть охарактеризовано такими параметрами:
1. амплитудой колебаний, т.е. величиной наибольшего отклонения от положения равновесия;
2. периодом колебаний, т.е. временем одного полного колебания; величина, обратная периоду называется частотой;
3. законом изменения колеблющейся величины со временем; гармоническое колебание происходит по закону синуса или косинуса;
4. фазой колебаний, характеризующей состояние колебаний в любой момент времени.
Гармоническое колебание может быть представлено в трех видах: графическом, аналитическом и векторным.
                 х(t)
t
Рис.5.1
| Графическое представление колебаний изображено на рис.5.1. Аналитическое представление гармонических колебаний не менее известно: x (t) = A sin (wt + j), (5-1) где j - начальная фаза колебаний, а весь аргумент синуса (wt + j) - фаза колебания, |
А - амплитуда колебаний, а w = 2p/ T - угловая частота колебаний (Т - период колебаний).
| А w j Рис.5.2 | Наконец, в векторном представлении колебание представляется в виде вектора, длина которого пропорциональна амплитуде колебаний (рис.5.2). Сам вектор вращается в плоскости чертежа с угловой скоростью w вокруг оси, перпендикулярной этой плоскости и проходящей через начало вектора колебания. Первоначальное отклонение вектора от горизонтали изображает начальную фазу колебания. |
Этот вид представления колебаний особенно удобен для сложения колебаний, когда результирующее колебание находится как векторная сумма всех слагаемых.
|
|
