
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение энергии по степеням свободы молекулСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Термодинамика – наука о наиболее общих свойствах физических макросистем, находящихся в состоянии термодинамического равновесия, и о процессах перехода между этими состояниями. Термодинамика построена на основе фундаментальных начал (законов), которые являются обобщением большого числа наблюдений и выполняются независимо от конкретной природы тел, образующих систему. Однако рассматривая основные понятия термодинамики, мы будем использовать и статистическую интерпретацию. Основными понятиями термодинамики являются такие понятия как состояние, процесс, цикл, внутренняя энергия, работа, количество теплоты, теплоёмкость, энтропия, свободная энергия, энтальпия, функция Гиббса. Среднюю кинетическую энергию движения молекулы идеального газа можно определить по формуле:
Число степеней свободыi определяется числом независимых координат и осей, описывающих движение частицы в пространстве. На каждую степень свободы статистической системы приходится одна и та же энергия, равная Энергия – величина аддитивная. Поэтому среднюю кинетическую энергию одного моля молекул можно определить, усреднив энергии всех частиц одного моля:
Среднюю кинетическую энергию любого количества идеального газа можно определить, усреднив энергии всех рассматриваемых частиц. Учитывая, что количество молекул в одном моле вещества очень велико, следовательно, средние кинетические энергии разных молей молекул практически одинаковы. Тогда средняя кинетическая энергия любого количества вещества может быть определена по формуле:
Внутренняя энергия Под внутренней энергией системы понимают полную суммарную энергию всех её структурных элементов. Внутренняя энергия идеального газа складывается только из кинетических энергий молекул, так как потенциальной энергией их взаимодействия можно пренебречь. Внутренняя энергия идеального газа U для любого количества молей n может быть определена через среднюю кинетическую энергию, определяемую формулой (9-3). Так как средняя кинетическая энергия идеального газа зависит только от температуры и числа степеней свободы молекулы, то и внутренняя энергия идеального газа также зависит от температуры и числа степеней свободы молекулы:
Изменение внутренней энергии идеального газа определяется только изменением температуры и не зависит ни от давления, ни от объёма:
Изменить внутреннюю энергию газа можно, например, совершив над ним работу. Но независимо от того, каким способом совершают работу, изменение внутренней энергии идеального газа зависит только от изменения температуры. Другими словами, изменение внутренней энергии зависит только от параметров начального и конечного состояния, а именно от температуры начального Т1 и конечного состояния Т 2, и не зависит от процесса перехода из начального в конечное состояние. Поэтому внутренняя энергия – функция состояния. Если газ вернули в первоначальное состояние, то изменение внутренней энергии равно нулю. Для элементарного процесса
Рассмотрим сжатие идеального газа, находящегося под поршнем (рис.9.1). Под действием внешней силы
Поскольку направление силы и перемещения совпадают, то
а работа внешней силы по сжатию газа равна Для определения работы по перемещению поршня на значительную величину
Работа газа (или над газом) зависит от процесса (т.е. от последовательности промежуточных состояний) и поэтому является функцией процесса. Работа не является полным дифференциалом, отсюда и обозначение элементарной работы
Рассмотрим изохорический процесс. При изохорическом процессе объём газа не изменяется, приращение объёма равно нулю, следовательно, работа газа равна нулю. Поскольку работу в любом случае можно определить, пользуясь формулой (9-8), для математической интерпретации работы удобно изображать любой процесс на диаграмме (P,V). Работа на такой диаграмме равна площади фигуры под кривой, изображающей тот или иной процесс, происходящий с газом. Рассмотрим изобарический процесс (рис. 9.2). Используя формулу (9-8) найдём работу газа при переходе из состояния 1 в состояние 2: Так как для данного количества вещества давление остаётся постоянным при изобарическом процессе, то его можно вынести за знак интеграла, тогда получим:
Используя рис.9.2, можно записать работу через указанные параметры состояния:
При изобарическом сжатии конечный объём меньше начального и работа газа отрицательна, то есть газ препятствует сжатию. Формула (9-7) позволяет выразить физический смысл молярной постоянной R. Для одного моля вещества (
Используя закон Бойля- Мариотта:
Рассмотренные примеры подтверждают, что работа является функцией процесса. Первое начало термодинамики Первое начало термодинамики учитывает энергетический баланс системы. В этом суть первого начала термодинамики. Можно сказать, что первое начало термодинамики является законом сохранения энергии для термодинамических систем. Для элементарного процесса первое начало термодинамики можно записать следующим образом:
|
||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 684; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.110.5 (0.009 с.) |

 (9-1)
(9-1) . В этом состоит суть теоремы о равнораспределении тепловой энергии по степеням свободы. Для сложных молекул, состоящих из нескольких атомов, число степеней свободы увеличивается за счёт вращательных и колебательных. Если пренебречь изменением потенциальной энергии взаимодействия частиц, то молекулы можно рассматривать как «жёсткие». Для жестких двухатомных молекул число степеней свободы i равно 5, из них 3 – поступательных (три независимые координаты х,y,z, описывающие положение частицы в пространстве) и 2 вращательных. (две независимых оси вращения). Для жёстких трёхатомных и многоатомных молекул число степеней свободы равно 6, из них 3 поступательных и 3 вращательных. Для жёстких одноатомных молекул число степеней свободы равно 3 и все они поступательные.
. В этом состоит суть теоремы о равнораспределении тепловой энергии по степеням свободы. Для сложных молекул, состоящих из нескольких атомов, число степеней свободы увеличивается за счёт вращательных и колебательных. Если пренебречь изменением потенциальной энергии взаимодействия частиц, то молекулы можно рассматривать как «жёсткие». Для жестких двухатомных молекул число степеней свободы i равно 5, из них 3 – поступательных (три независимые координаты х,y,z, описывающие положение частицы в пространстве) и 2 вращательных. (две независимых оси вращения). Для жёстких трёхатомных и многоатомных молекул число степеней свободы равно 6, из них 3 поступательных и 3 вращательных. Для жёстких одноатомных молекул число степеней свободы равно 3 и все они поступательные. , где
, где  - число молекул в одном моле вещества (число Авогадро). Учитывая, что произведение числа Авогадро и постоянной Больцмана равно универсальной газовой постоянной, получим энергию одного моля молекул:
- число молекул в одном моле вещества (число Авогадро). Учитывая, что произведение числа Авогадро и постоянной Больцмана равно универсальной газовой постоянной, получим энергию одного моля молекул: (9-2)
(9-2) (9-3)
(9-3) (9-4)
(9-4) (9-5)
(9-5) . Можно внести постоянные ν и R под знак дифференциала
. Можно внести постоянные ν и R под знак дифференциала  . Таким образом, изменение внутренней энергии является полным дифференциалом величины, стоящей в скобках, и этот факт может служить признаком функции состояния.
. Таким образом, изменение внутренней энергии является полным дифференциалом величины, стоящей в скобках, и этот факт может служить признаком функции состояния. 9.3. Работа газа при его расширении
9.3. Работа газа при его расширении переместим поршень на бесконечно малую величину
переместим поршень на бесконечно малую величину 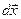 , настолько малую, что будем считать силу
, настолько малую, что будем считать силу  .
. 
 (9-6)
(9-6) . Газ, находящийся под поршнем, препятствует сжатию и давит на поршень силой
. Газ, находящийся под поршнем, препятствует сжатию и давит на поршень силой  , равной по величине, противоположной по направлению и приложенной к поршню (рис.4.1). Элементарная работа самого газа
, равной по величине, противоположной по направлению и приложенной к поршню (рис.4.1). Элементарная работа самого газа  . Так как сила
. Так как сила  и перемещение
и перемещение 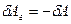 . Сила, действующая на единицу площади поверхности поршня S со стороны газа, есть давление газа Р. Поэтому можно выразить величину силы
. Сила, действующая на единицу площади поверхности поршня S со стороны газа, есть давление газа Р. Поэтому можно выразить величину силы  через давление:
через давление:  . Тогда элементарная работа газа будет равна:
. Тогда элементарная работа газа будет равна:  . Но
. Но  есть величина приращения объёма газа. Тогда элементарная работа газа равна:
есть величина приращения объёма газа. Тогда элементарная работа газа равна: , (9-7)
, (9-7) .
. , в результате которой объём газа изменяется на
, в результате которой объём газа изменяется на  , нужно учесть процесс, происходящий с газом. Работу в этом случае определяют через интеграл:
, нужно учесть процесс, происходящий с газом. Работу в этом случае определяют через интеграл: (9-8)
(9-8) Рассмотрим работу, совершаемую газом, при различных процессах. Будем обозначать в дальнейшем элементарную работу газа просто через
Рассмотрим работу, совершаемую газом, при различных процессах. Будем обозначать в дальнейшем элементарную работу газа просто через  ), и отрицательной, если газ сжимают (
), и отрицательной, если газ сжимают ( ).
). .
. . Обозначим
. Обозначим 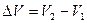 . С учётом этой записи работа при изобарическом процессе определяется по формуле:
. С учётом этой записи работа при изобарическом процессе определяется по формуле: (9-9)
(9-9) . Такую же формулу мы получим, находя площадь заштрихованного прямоугольника. Часто бывает удобно выражать работу через изменение температуры. Для этого нужно использовать уравнение состояния идеального газа (уравнение Менделеева – Клапейрона) для 1 и 2 состояний:
. Такую же формулу мы получим, находя площадь заштрихованного прямоугольника. Часто бывает удобно выражать работу через изменение температуры. Для этого нужно использовать уравнение состояния идеального газа (уравнение Менделеева – Клапейрона) для 1 и 2 состояний:  и
и  . Вычитая из второго уравнения первое, получим:
. Вычитая из второго уравнения первое, получим: (9-10)
(9-10) ) работа определяется как
) работа определяется как 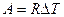 . Отсюда ясен физический смысл R, которая определяется работой изобарического расширения одного моля идеального газа при изменении температуры на один кельвин.
. Отсюда ясен физический смысл R, которая определяется работой изобарического расширения одного моля идеального газа при изменении температуры на один кельвин. Рассмотрим изотермический процесс (рис.9.3). При изотермическом процессе температура остаётся постоянной, а давление и объём связаны между собой обратно пропорциональной зависимостью. В этом случае, используя формулу (9-8) для определения работы, уже нельзя вынести давление за знак интеграла. Давление выразим из уравнения Менделеева – Клапейрона:
Рассмотрим изотермический процесс (рис.9.3). При изотермическом процессе температура остаётся постоянной, а давление и объём связаны между собой обратно пропорциональной зависимостью. В этом случае, используя формулу (9-8) для определения работы, уже нельзя вынести давление за знак интеграла. Давление выразим из уравнения Менделеева – Клапейрона:  . Подставим правую часть этого уравнения в (9-8) и вынесен за знак интеграла все постоянные:
. Подставим правую часть этого уравнения в (9-8) и вынесен за знак интеграла все постоянные: . Учитывая, что разность логарифмов есть логарифм отношения, получим:
. Учитывая, что разность логарифмов есть логарифм отношения, получим: (9-11)
(9-11) , можем выразить работу и через отношение давлений:
, можем выразить работу и через отношение давлений: (9-12)
(9-12) . Работа самого газа связана с работой внешних сил равенством
. Работа самого газа связана с работой внешних сил равенством  . Тогда математическая запись первого начала термодинамики будет иметь вид:
. Тогда математическая запись первого начала термодинамики будет иметь вид: 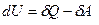 . Однако в тех случаях, когда происходит теплообмен и система получает (или отдаёт тепло), удобно записывать первое начало в виде:
. Однако в тех случаях, когда происходит теплообмен и система получает (или отдаёт тепло), удобно записывать первое начало в виде: (9-13)
(9-13)


