
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Термодинамический подход к описанию молекулярных явлений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Термодинамические системы. а) Система открытая, если возможен энергообмен и обмен веществом. б) Система закрытая, если энергообмен возможен, а обмен веществом невозможен. Закрытые системы дополнительно подразделяются по признаку возможности осуществления энергообмена следующим образом: а) Система замкнутая, если энергообмен возможен, но обмен с внешней средой путем совершения механической работы невозможен. б) Система изолированная, если невозможен какой-либо обмен системы с окружающей средой. в) Система адиабатная, если отсутствует теплообмен системы с окружающей средой. Задание системы с помощью уравнений состояния. Уравнение состояния — уравнение, связывающее между собой термодинамические (макроскопические) параметры системы, такие, как температура, давление, объём, химический потенциал и др. Термическое уравнение состояния связывает макроскопические параметры системы
Калорическое уравнение состояния показывает, как внутренняя энергия выражается через давление, объем и температуру.
Каноническое уравнение представляет собой выражение для одного из термодинамических потенциалов (внутренней энергии, энтальпии, свободной энергии или потенциала Гиббса) через независимые переменные, относительно которых записывается его полный дифференциал
Нулевое начало термодинамики. макроскопическая система, находящаяся в неизменных внешних условиях, всегда приходит самопроизвольно в состояние термодинамического равновесия, которое характеризуется тем, что: прекращаются всякие макроскопические изменения в системе; каждый параметр, характеризующий макроскопическое свойство системы, имеет постоянное во времени значение; система, перешедшая в состояние термодинамического равновесия, сколь угодно долго остаётся в этом состоянии; для нарушения равновесия необходимы внешние воздействи Понятие термодинамического равновесия. Термодинамическое равновесие — состояние системы, при котором остаются неизменными по времени макроскопические величины этой системы в условиях изолированности от окружающей среды Принцип термодинамической аддитивности. Согласно ему, все величины, описывающие термодинамические свойства систем могут принадлежать к одному классу аддитивности (аддитивные, неаддитивные). Примером аддитивных величин являются числа частиц в системе, объем V, Энергия, полная энергия системы ε, теплоемкость С. Примерами неаддитивных величин являются удельная энергия. Удельный объем V = V/N, температура и т.д. аддитивность объёма означает, что объём целого тела равен сумме объёмов составляющих его частей. Квазистатические процессы. Квазистатический процесс в термодинамике — идеализированный процесс, состоящий из непрерывно следующих друг за другом состояний равновесия. Такие процессы называют также квазиравновесными, так как систему в каждый момент времени можно считать находящейся в состоянии термодинамического равновесия Обратимые и необратимые процессы. Процесс называют обратимым, если он допускает возвращение рассматриваемой системы из конечного состояния в исходное через ту же последовательность промежуточных состояний, что и в прямом процессе, но проходимую в обратном порядке. При этом в исходное состояние возвращается не только система, но и среда. Обратимый процесс возможен, если и в системе, и в окружающей среде он протекает равновесно Необратимые процессы могут протекать самопроизвольно только в одном направлении; таковы диффузия, теплопроводность, вязкое течение и другое
Теплоемкость системы. Теплоемкость идеального газа. Связь теплоемкости газа с числом степеней свободы молекул. Уравнение Майера. Политропический процесс. Уравнение политропы и его частные случаи. Классическая теория теплоемкости твердых тел. Закон Дюлонга и Пти. Фундаментальные трудности классической теории теплоемкости. Квантовая теория теплоемкости с учетом внутренних движений. Закон Дебая. Температура Дебая. Теплоемкость системы. Теплоемкостью системы называется отношение бесконечно малого количества тепла Теплоемкость идеального газа - отношение количества теплоты, сообщённого газу, к изменению температуры δТ, которое при этом произошло. Связь теплоемкости газа с числом степеней свободы молекул. Уравнение Майера. Запишем выражение 1 начала термодинамики для 1 моля газа Политропический процесс – это процесс в котором теплоемкость остается постоянной. Уравнение политропы и его частные случаи. Классическая теория теплоемкости твердых тел. Простейшей моделью кристалла является правильно построенная кристаллическая решетка, в узлах которой помещаются атомы, принимаемые за материальные точки. Атомы совершают тепловые колебания около положения положений равновесия. Если колебания малы, то они будут гармоническими. Энергия каждого атома слагается из кинетической и потенциальной. На каждую степень свободы приходится в среднем кинетическая энергия Закон Дюлонга и Пти. Произведение удельной теплоемкости химического элемента в твердом состоянии на его атомную массу приблизительно одинаково для всех элементов и составляет около 6 кал/(К моль). Мы видим, что правило Дюлонга и Пти находит простое объяснение в классической теории теплоемкостей. Вывод показывает, что в правиле Дюлонга и Пти речь идет о молярной теплоемкости при постоянном объеме. Фундаментальные трудности классической теории теплоемкости. Квантовая теория теплоемкости с учетом внутренних движений. Закон Дебая. Вблизи абсолютного нуля теплоемкость кристаллической решетки твердого тела пропорциональна кубу абсолютной температуры. Температура Дебая – физическая константа вещества, характеризующая многие свойства твердых тел – теплоемкость, электропроводность, теплопроводность, уширение линий ренгнновских спектров, упругие свойства и т.п. Определяется как
18. Первое и второе начала термодинамики. Дифференциальная форма первого начала. Две теоремы Карно. Понятие энтропии термодинамической системы. Микро- и макросостояния системы. Термодинамическая вероятность. Энтропия и вероятность. Закон возрастания энтропии в неравновесной изолированной системе. Неравенство Клаузиуса. Формулировка Клаузиуса и Томсона (Кельвина) второго начала термодинамики. Первое и второе начала термодинамики. Первое начало термодинамики - закон сохранения и превращения энергии, которым сопровождаются термодинамические процессы – количество тепла, подводимого к системе, идет на изменение ее внутренней энергии и работу, производимую системой против внешних сил: Второе начало термодинамики: в изолированной системе возможны только такие процессы, при которых энтропия системы возрастает или невозможен процесс, единственным результатом которого является превращение в работу теплоты, полученной от нагревателя: Дифференциальная форма первого начала. Две теоремы Карно. Первая теорема Карно. КПД обратимого цикла Карно, осуществляемого между двумя источниками теплоты, не зависит от свойств рабочего вещества, с помощью которого этот цикл осуществляется. Вторая теорема Карно. КПД необратимого цикла Карно всегда меньше обратимого цикла Карно, осуществляемого между одними и теми же источниками теплоты, имеющими постоянные, но разные температуры. Понятие энтропии термодинамической системы. Энтропия - физическая величина, элементарное изменение которой при переходе системы из одного состояния в другое равно по- лученному или отданному количеству теплоты, деленному на темпе- ратуру, при которой произошел этот процесс: Микро- и макросостояния системы. Микросостояние – это самое точное возможное описание термодинамической системы, детально охарактеризованное кубическими ячейками пространства координат и пространства импульсов, описывающее наиболее точное задание состояния частиц. Макросостояние – это состояние термодинамической системы, заданное и охарактеризованное с помощью макроскопических параметров. Термодинамическая вероятность (или статический вес) — число способов, которыми может быть реализовано состояние физической системы. Термодинамическая вероятность (обозначается W) равна числу микросостояний, реализующих данное макросостояние, из чего следует, что Энтропия и вероятность. Термодинамическая вероятность связана с одной из основных макроскопических характеристик системы энтропией S соотношением Больцмана: Закон возрастания энтропии в неравновесной изолированной системе. Энтропия адиабатически изолированной системы не может убывать, она либо возрастает, либо остается постоянной. Неравенство Клаузиуса. Количество теплоты, полученное системой при любом круговом процессе, деленное на абсолютную температуру, при которой оно было получено, неположительно. Формулировка Клаузиуса и Томсона (Кельвина) второго начала термодинамики. В 1851 г. У. Томсон (лорд Кельвин) предложил другую формулировку этого закона (постулат Кельвина): “Невозможно осуществить круговой процесс, единственным результатом которого было бы превращение в работу теплоты отнятой у какоголибо теплового резервуара, без всяких изменений в других телах”. Постулат Кельвина можно представить в следующем виде (по В. Оствальду): “Невозможно построить циклически действующую тепловую машину, которая производила бы работу за счет охлаждения какоголибо тела без всяких изменений в других телах”.
Реальные газы и жидкости. Неидеальный классический одноатомный газ. Парная корреляционная функция и её связь с энергией. Реальные газы. Уравнение Ван-дер-Ваальса. Внутренняя энергия газа Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса. Критическое состояние. Область двухфазных состояний. Метастабильные состояния. Силы межмолекулярного взаимодействия. Потенциал Леннарда-Джонса. Эффект Джоуля-Томсона. Метод получения низких температур. Реальные газы и жидкости. Как мы видели, идеальный газ — это упрощенная модель реальных газов. В этой модели не учитываются объем молекул и силы взаимодействия между ними. Между тем молекулы реальных газов занимают определенный объем и взаимодействуют между собой. При больших давлениях и низких температурах становится заметным влияние собственных объемов молекул и сил взаимодействия между ними. При этих условиях уравнение Клапейрона—Менделеева и законы Бойля—Мариотта, Гей-Люссака, Шарля непригодны для описания состояния реальных газов. В 1873 г. голландский физик И. Ван дер-Ваальс ввел в уравнение Клапейрона—Менделеева поправки на размер молекул и на действие сил притяжения между ними. И. Ван-дер-Ваальс предложил модель реального газа, в которой молекулы принимаются за твердые шарики диаметром d и занимают хоть малый, но некоторый объем. Молекулы не только отталкиваются при соударениях, но еще и притягиваются друг к другу сравнительно слабыми силами на расстояниях, сравнимых с размерами молекул. Реальной жидкостью называют жидкость, обладающую вязкостью (свойство жидкости сопротивляться сдвигу ее слоев). Уравнение Ван-дер-Ваальса. Внутренняя энергия газа Ван-дер-Ваальса. Энергия одного моля газа Ван–дер–Ваальса слагается из внутренней энергии молекул, составляющих газ: кинетической энергии теплового движения центра масс молекул Изотермы Ван-дер-Ваальса. Проанализируем изотермы уравнения Ван–дер–Ваальса – зависимости Р от V для реального газа при постоянной температуре. Умножив уравнение Ван-дер-Ваальса на V 2 и раскрыв скобки, получаем PV 3 – (RT + bP) vV 2 + av2V - abv3 = 0. Поскольку данное уравнение имеет третью степень относительно V, а коэффициенты при V действительны, то оно имеет либо один, либо три вещественных корня, т.е. изобара Р = const пересекает кривую Р = Р(V) в одной или трех точках, как это изображено на рисунке. Причем с повышением температуры мы перейдем от немонотонной зависимости Р = Р(V) к монотонной однозначной функции. Изотерма при Ткр, которая разделяет немонотонные T < Tкр и монотонные T > Ткр изотермы, соответствует изотерме при критической температуре. При температуре выше критической зависимость Р = Р(V) является однозначной монотонной функцией объема. Это означает, что при T > Ткр вещество находится только в одном, газообразном состоянии, как это имело место у идеального газа. При температуре газа ниже критической такая однозначность исчезает, а это означает возможность перехода вещества из газообразного в жидкое и наоборот. На участке АСВ изотермы Т1 давление растет с увеличением объема (dP/dV) > 0. Данное состояние неустойчиво, поскольку здесь должны усиливаться малейшие флуктуации плотности. Поэтому область ВСА не может устойчиво существовать. В областях DLB и AGE давление падает с увеличением объема (dP/dV)Т < 0 – это необходимое, но не достаточное условие устойчивого равновесия. Эксперимент показывает, что система переходит из области устойчивых состояний GE (газ) в область устойчивых состояний LD(жидкость) через двухфазное состояние (газ – жидкость) GL вдоль горизонтальной изотермы GCL. При квазистатическом сжатии, начиная с точки G, система распадается на 2 фазы – жидкость и газ, причем плотности жидкости и газа остаются при сжатии неизменными и равными их значениям в точках L и G соответственно. При сжатии количество вещества в газообразной фазе непрерывно уменьшается, а в жидкой фазе – увеличивается, пока не будет достигнута точка L, в которой все вещество перейдет в жидкое состояние. Критическое состояние. Наличие критической точки на изотерме Ван–дер–Вальса означает, что для каждой жидкости существует такая температура, выше которой вещество может существовать только в газообразном состоянии. Критическую точку K мы определили как точку перегиба критической изотермы, в которой касательная к изотерме горизонтальна. Метастабильные состояния. При специальных условиях могут быть реализованы состояния, изображаемые участками GA и BL. Эти состояния называются метастабильными: пересыщенный пар и перегретая жидкость соответственно.
Силы межмолекулярного взаимодействия. Межмолекулярное взаимодействие — взаимодействие между молекулами и/или атомами, не приводящее к образованию ковалентных (химических) связей. Межмолекулярное взаимодействие имеет электростатическую природу. Предположение о его существовании было впервые использовано Я. Д. Ван-дер-Ваальсом в 1873 году для объяснения свойств реальных газов и жидкостей. Иными словами, эти взаимодействия существенно слабее ковалентных и не приводят к существенной перестройке электронного строения взаимодействующих частиц. На больших расстояниях преобладают силы притяжения, которые могут иметь ориентационную, поляризационную (индукционную) и дисперсионную природу. На малых расстояниях начинают преобладать силы отталкивания электронных оболочек частиц. Потенциал Леннарда-Джонса. Во многих вопросах теории газов к хорошим результатам приводит следующая аппроксимация функции U(x): Эффект Джоуля-Томсона - называется изменение температуры газа при адиабатическом дросселировании — медленном протекании газа под действием постоянного перепада давлений сквозь дроссель (пористую перегородку). Данный эффект является одним из методов получения низких температур. Метод получения низких температур. Существует 3 основных метода получения низких температур: 1) испарение жидкостей (холодильные машины, в том числе домашние холодильники), 2) эффект Джоуля-Томсона при температуре меньше Тi, 3) обратимое адиабатическое расширение газов с совершением внешней работы. Для получения низких температур и непрерывного сжижения газов созданы специальные циклы, которые используют комбинированные методы.
Термодинамические потенциалы. Метод термодинамических потенциалов. Условия равновесия и устойчивости однородной системы. Термодинамические тождества. Термодинамическое описание газов, магнетиков, диэлектриков. Химический потенциал, электрическая поляризация, магнитная восприимчивость. Термодинамические потенциалы. Особенно важное значение в термодинамике имеют две функции состояния: свободная энергия ψ, введенная Гельмгольцем, и термодинамический потенциал Ф, введенный Гиббсом. Эти функции состояния определяются выражениями
Для их дифференциалов легко получить
Исходя из всех этих выражений будем рассматривать внутреннюю энергию U как функцию аргументов S и V, энтальпию I — как функцию S и Р, свободную энергию Аналогично, Условия равновесия и устойчивости однородной системы. Специальный термодинамический анализ позволяет показать, что из соображений термодинамической устойчивости системы для любого вещества должны выполняться следующие соотношения: Термодинамические тождества. Основные уравнения термодинамики для диэлектрика в электрическом поле будет: а) при независимой электрической переменной D Химический потенциал, электрическая поляризация, магнитная восприимчивость. Химический потенциал – термодинамическая функция, применяемая при описании состояния систем с переменным числом частиц. Определяет изменение термодинамических потенциалов (энергии Гиббса, внутренней энергии, энтальпии и т.д.) при изменении числа частиц в системе. Представляет собой энергию добавления одной частицы в систему без совершения работы. Применяются для описания материального взаимодействия. Определение химического потенциала можно записать в виде: Электрическая поляризация - под действием внешнего поля положение или движение зарядов внутри молекулы слегка изменяется таким образом, что положительные заряды смещаются в направлении электрического поля, а отрицательные в противоположном направлении. Магнитная восприимчивость – определяется отношением намагниченности единицы объема вещества к напряженности намагничивающего магнитного поля. По своему смыслу восприимчивость является величиной безразмерной.
Твердые тела. Главным отличием ТТ от газообразных и жидких тел является способность сохранять не только объем, но и форму. Однако некоторые вещества по признаку сохранения формы должны быть отнесены к ТТ, но во всем остальном они не отличаются от жидкостей. Это аморфные тела: стекло, смолы, пластмассы. В-ва этого типа ведут себя как жидкости с аномально большой вязкостью, благодаря которой они при обычной и низкой температуре не могут течь, но при ее повышении вязкость умень-ся и они размягчаются и приобретают обычную для жид-тей способность течь. У «настоящих» ТТ такого размягчения не происходит. Хотя они и переходят при повышении темп-ры в жидкое состояние, но происходит этот переход не при постепенном пов-ии температуры, а скачком при определенной температуре плавления. Это важная особенность, отличающая ТТ от аморфных. Свойства ТТ обусловлены тем. Что атомы в них расположены не хаотично, как в жидкостях и газах, а в определенном характерном для каждого вещества порядке, причем в ТТ такая упорядоченность распространяется на весь объем (дальний порядок). Такие тела с правильным расположением частиц называются кристаллическими. В аморфных же упорядоченное расположение частиц распространяется только на соседние атомы (ближний порядок).Кристаллическая решетка- структура, для которой характерно регулярное расположение частиц с периодической повторяемостью в 3-х измерениях. Узлы крист решетки- точки, в которых расположены частицы, а точнее точки относительно которых частицы совершают колебания. Монокристалл- ТТ, частицы которого образуют единую крист решетку. Поликристалл- ТТ, имеющее мелкокристаллическую структуру, т.е. состоящее из множества беспорядочно ориентированных мелких кристаллических зерен. Если вдоль разных направлений свойства тела различны. То такое тело обладает анизотропией. Анизотропией обладают монокристаллы. Если при помощи какого-либо механ воздействия придать кристаллическим зернам поликристалла некоторую упорядоченность, то такой материал будет наз-ся текстурированным и будет проявлять некоторые анизотропные свойства. Анизотропия объясняется следующим: если провести через узлы решетки плоскости в разных направлениях, то густота расположения атомов на этих плоскостях различна. Существует 2 признака для классификации кристаллов: 1) физический 2) кристаллографический. 1) по природе частиц, расположенных в узлах КР, и характеру сил взаимодействия между ними: ионный (в узлах –поочередно ионы противоположного знака), атомный (нейтральные атомы), молекулярный, металлический (положительные ионы металла). Можно по элект свойствам: проводники (золото), пп (кремний), диэлектрики (алмаз). 2) В данном случае важна только пространственная периодичность в расположении частиц, поэтому можно отвлечься от их внутренней структуры, рассматривая частицы как геометрические точки. Характерной особенностью кр-ла яв-ся геометрически правильное расположение его частиц. Кр-ал, следовательно, имеет прерывную периодическую структуру. С геометрической точки зрения такое периодически повторяющееся расположение частиц можно осуществить с помощью операции параллельного перемещения, которое наз-ся трансляцией. Решетка- сложное образование, ее целесообразно разбить на более простые подрешетки. Наиболее простой решеткой яв-ся решетка, состоящая из параллелепипедов как элементарной совокупности атомов. Выбрав начало координат в некотором узле такой решетки, радиус-вектор любого другого узла: r=n1a1+n2a2+n3a3, где n1n2n3—целые числа, а a1,a2,a3-длины ребер, называются основными периодами решетки. Векторы a1,a2,a3 наз-ся базисными, а их совокупность базисом решетки. Параллелепипед с ребрами a1,a2,a3 вместе с атомами в его вершинах наз-ся элементарной ячейкой КР. Если в формуле числа n1n2n3 пробегают всевозможные целочисленные значения от -∞ до +∞, то рад-в r походит все узлы решетки. Такая решетка называется примитивной или решеткой Браве, а ее элементарная ячейка- примитивной ячейкой. Конкретная КР, вообще говоря, не может быть представлена в виде одной решетки Браве, а явл-ся совокупностью нескольких решеток Браве. Благодаря правильной, периодически повторяющейся картине расположения атомов К обладает симметрией. Это свойство заключается в том, что в результате некоторых мыслительных операций система частиц К совмещается сама с собой- переходит в положение не отличимое от исходного. Симметрию К удобно представить как совокупность отдельных элементов симметрии: ось сим-ии, плоскость сим, центр сим т зеркально- поворотная ось сим-ии. Если к обладает ОС, то он может быть совмещен с самим собой путем поворота на некоторый угол. Если одна половина К сов-ся с другой при отражении в некоторой плоскости, то ПС. ЦС- точка в К, обладающая тем свойством, что при замене р-в r на –r, кристалл переходит в состояние, не отличимое от исходного. ПЗО- если кристалл можно совместить с самим собой, повернув его на некоторый угол вокруг оси т отразив затем в плоскости, перпендикулярной к этой оси. Совокупность всех элементов симметрии, которыми обладает данная КР, называется пространственной группой этой решетки. Решетка также обладает трансляционной симметрией, т.е. способна совмещаться с собой в результате поступательного перемещения. Если сместить ее на вектор r, то решетка совпадет сама с собой, поэтому r- вектор трансляции. Т.е. решетка может быть получена из любого узла, если его подвергнуть всевозможным трансляциям вдоль базисных векторов. Перечисленные элементы в различных КР могут комбинироваться по- разному. Рассмотрение показало, что существуют всего 32 возможных комбинаций элементов симметрии (Гадолин). Каждая из них называется классом симметрии. Выделяют: простая (атомы в узлах КР), объемноцентрированная (+ в центре), базоцентрированная (в узлах + в серединах оснований), гранецентрированная (в узлах + в середине каждой грани.Введение кристаллографических символов связано с необходимостью обозначить направления в К. Пусть внутри К есть точка с координатами (x,y,z), тогда кристаллогр символы h:k:l=
|
||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 949; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.46.129 (0.015 с.) |




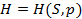


 , полученного системой, к соответствующему приращению
, полученного системой, к соответствующему приращению  ее температуры:
ее температуры: 
 . Молярная теплоемкость определяется лишь числом степеней свободы и не зависит от температуры. Это справедливо для одноатомных газов. Уже у двухатомных газов число степеней свободы, проявляющееся в теплоемкости зависит от Т.
. Молярная теплоемкость определяется лишь числом степеней свободы и не зависит от температуры. Это справедливо для одноатомных газов. Уже у двухатомных газов число степеней свободы, проявляющееся в теплоемкости зависит от Т. (1). Если газ нагревается при
(1). Если газ нагревается при  , то
, то  , тогда
, тогда  , т.е. молярная теплоемкость газа при постоянном объеме CV равна изменению внутренней энергии 1 моля газа при повышении его температуры на 1 К.
, т.е. молярная теплоемкость газа при постоянном объеме CV равна изменению внутренней энергии 1 моля газа при повышении его температуры на 1 К.  , тогда
, тогда  . Если газ нагревается при постоянном давлении, то (1) перепишется
. Если газ нагревается при постоянном давлении, то (1) перепишется  . Учитывая все это и продифференцировав уравнение Клапейрона-Менделеева
. Учитывая все это и продифференцировав уравнение Клапейрона-Менделеева  по Т при p=const, получим
по Т при p=const, получим  - уравнение Майера.
- уравнение Майера. , где
, где  - показатель политропы.
- показатель политропы.  - уравнение адиабаты,
- уравнение адиабаты,  - уравнение изотермы,
- уравнение изотермы,  - уравнение изобары,
- уравнение изобары,  - уравнение изохоры.
- уравнение изохоры.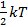 , при гармонических колебаниях на одну степень свободы приходится в среднем такая же потенциальная энергия. Т.о. среднее значение полной энергии на одну колебательную степень свободы
, при гармонических колебаниях на одну степень свободы приходится в среднем такая же потенциальная энергия. Т.о. среднее значение полной энергии на одну колебательную степень свободы  .
. ,
,  - постоянная Планка,
- постоянная Планка,  – максимальная частота колебаний атомов твердого тела,
– максимальная частота колебаний атомов твердого тела,  - постоянная Больцмана. Температура Дебая приближенно указывает температурную границу, ниже которой начинают сказываться квантовые эффекты.
- постоянная Больцмана. Температура Дебая приближенно указывает температурную границу, ниже которой начинают сказываться квантовые эффекты. , где
, где  - изменение внутренней энергии системы; Q - элементарное количество тепла, подводимого к системе; A - элементарная работа, совершаемая системой.
- изменение внутренней энергии системы; Q - элементарное количество тепла, подводимого к системе; A - элементарная работа, совершаемая системой. или
или 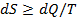 .
. , где dU - изменение внутренней энергии системы; δQ - элементарное количество тепла, подводимого к системе; δA - элементарная работа, совершаемая системой.
, где dU - изменение внутренней энергии системы; δQ - элементарное количество тепла, подводимого к системе; δA - элементарная работа, совершаемая системой. .
. .
. .
. , где k — постоянная Больцмана.
, где k — постоянная Больцмана. .
. - уравнение Ван-дер-Ваальса для 1 моля реального газа.
- уравнение Ван-дер-Ваальса для 1 моля реального газа. , равной, и потенциальной энергии взаимного притяжения молекул. Потенциальная энергия взаимодействия равна:
, равной, и потенциальной энергии взаимного притяжения молекул. Потенциальная энергия взаимодействия равна:  . Знак «минус» указывает на то, что между молекулами действуют силы притяжения; Vm – молярный объем, Vm = V/µ, v = m/m. Полная энергия одного моля газа Ван-дер-Ваальса определяется соотношением
. Знак «минус» указывает на то, что между молекулами действуют силы притяжения; Vm – молярный объем, Vm = V/µ, v = m/m. Полная энергия одного моля газа Ван-дер-Ваальса определяется соотношением  . Если СV не зависит от температуры, то имеем для одного моля
. Если СV не зависит от температуры, то имеем для одного моля  .
. Область двухфазных состояний. На рисунке схематично изображено семейство реальных изотерм. Жирная кривая ALKG, соединяющая концы горизонтальных участков изотерм, делит плоскость VP на две области. Область между кривой ALKG и изобарой P=0 соответствует двухфазным состояниям вещества. Это значит, что каждая точка этой области изображает такое состояние вещества, в котором оно не является физически однородным, а состоит из жидкости и ее насыщенного пара. Ниже изобары P=0 двухфазное состояние невозможно, так как давление пара не может быть меньше нуля.
Область двухфазных состояний. На рисунке схематично изображено семейство реальных изотерм. Жирная кривая ALKG, соединяющая концы горизонтальных участков изотерм, делит плоскость VP на две области. Область между кривой ALKG и изобарой P=0 соответствует двухфазным состояниям вещества. Это значит, что каждая точка этой области изображает такое состояние вещества, в котором оно не является физически однородным, а состоит из жидкости и ее насыщенного пара. Ниже изобары P=0 двухфазное состояние невозможно, так как давление пара не может быть меньше нуля. , где
, где  и
и 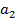 - постоянные. Она называется потенциалом Леннарда-Джонса. Первый член соответствует силам отталкивания, второй силам притяжения Ван-дер-Ваальса. Сила притяжения убывает обратно пропорционально седьмой степени расстояния. Первый член – это простая аппроксимация.
- постоянные. Она называется потенциалом Леннарда-Джонса. Первый член соответствует силам отталкивания, второй силам притяжения Ван-дер-Ваальса. Сила притяжения убывает обратно пропорционально седьмой степени расстояния. Первый член – это простая аппроксимация. (45.4)
(45.4) (45.5)
(45.5) (45.6)
(45.6)  (45.7). При изотермическом процессе dT = 0, а потому
(45.7). При изотермическом процессе dT = 0, а потому  . Отсюда
. Отсюда 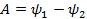 . Следовательно, свободная энергия есть функция состояния системы, убыль которой в квазистатическом изотермическом процессе дает работу, произведенную системой.
. Следовательно, свободная энергия есть функция состояния системы, убыль которой в квазистатическом изотермическом процессе дает работу, произведенную системой. как функцию Т и V, термодинамический потенциал Ф — как функцию Т и Р.
как функцию Т и V, термодинамический потенциал Ф — как функцию Т и Р.  (1). Такого рода соотношения называются каноническими уравнениями. Каноническое уравнение состояния, в какой бы из четырех форм оно ни было взято, содержит полные сведения о термическихи калорических свойствах вещества. Дифференцируем уравнения (1) и сравниваем их с предыдущими выражениями и получаем два следствия выведенных уравнений. Из определения функций ψ и Ф следует
(1). Такого рода соотношения называются каноническими уравнениями. Каноническое уравнение состояния, в какой бы из четырех форм оно ни было взято, содержит полные сведения о термическихи калорических свойствах вещества. Дифференцируем уравнения (1) и сравниваем их с предыдущими выражениями и получаем два следствия выведенных уравнений. Из определения функций ψ и Ф следует 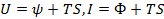 . Подставив сюда выражения для энтропии, получим
. Подставив сюда выражения для энтропии, получим  Эти уравнения называются уравнениями Гиббса — Гельмгольца. Далее, вторичным дифференцированием находим
Эти уравнения называются уравнениями Гиббса — Гельмгольца. Далее, вторичным дифференцированием находим  . Отсюда на основании известной теоремы анализа о перемене порядка дифференцирования следует
. Отсюда на основании известной теоремы анализа о перемене порядка дифференцирования следует  .
. ,
,  ,
,  . Эти и подобные им соотношения называются соотношениями взаимности или соотношениями Максвелла. Они постоянно используются для вывода различных соотношений между величинами, характеризующими термодинамически равновесные состояния системы. Такой метод вывода называется Методом термодинамических потенциалов.
. Эти и подобные им соотношения называются соотношениями взаимности или соотношениями Максвелла. Они постоянно используются для вывода различных соотношений между величинами, характеризующими термодинамически равновесные состояния системы. Такой метод вывода называется Методом термодинамических потенциалов. (1)
(1)  (2), т.е. во-первых изохорная теплоемкость сv всегда положительна и, во-вторых, в изотермическом процессе увеличение давления всегда приводит к уменьшению объема вещества. Условие (1) называют условием термической устойчивости, а условие (2) – условием механической устойчивости.
(2), т.е. во-первых изохорная теплоемкость сv всегда положительна и, во-вторых, в изотермическом процессе увеличение давления всегда приводит к уменьшению объема вещества. Условие (1) называют условием термической устойчивости, а условие (2) – условием механической устойчивости.
 , б) при независимой переменной P
, б) при независимой переменной P  , где
, где  - собственная внутренняя энергия единицы объема диэлектрика. в) при независимой переменной E, когда сопряженной ей величиной является поляризованность P
- собственная внутренняя энергия единицы объема диэлектрика. в) при независимой переменной E, когда сопряженной ей величиной является поляризованность P  , где
, где  - сумма собственной внутренней энергии поляризации диэлектрика и его потенциальной энергии в электрическом поле. г) при независимой переменной E, когда сопряженной ей величиной является электрическое смещение D
- сумма собственной внутренней энергии поляризации диэлектрика и его потенциальной энергии в электрическом поле. г) при независимой переменной E, когда сопряженной ей величиной является электрическое смещение D  , где
, где - внутренняя энергия диэлектрика с учетом его потенциальной энергии в поле без энергии поля в вакууме. Аналогичные уравнения для магнетиков могут быть получены простой заменой электрических величин магнитными.
- внутренняя энергия диэлектрика с учетом его потенциальной энергии в поле без энергии поля в вакууме. Аналогичные уравнения для магнетиков могут быть получены простой заменой электрических величин магнитными. , где
, где  - энергия системы,
- энергия системы,  - ее энтропия,
- ее энтропия,  - количество частиц в системе. Эта формула определяет, кроме химического потенциала, также давление и температуру. Для систем, состоящих из одной компоненты, можно доказать, что химический потенциал задается формулой
- количество частиц в системе. Эта формула определяет, кроме химического потенциала, также давление и температуру. Для систем, состоящих из одной компоненты, можно доказать, что химический потенциал задается формулой  , где
, где  - потенциал Гиббса.
- потенциал Гиббса. , где
, где  - намагниченность вещества под действие магнитного поля,
- намагниченность вещества под действие магнитного поля,  - напряженность магнитного поля. Иногда вводят понятие удельной магнитной восприимчивости, равной восприимчивости единицы массы вещества. В СИ удельная восприимчивость измеряется в обратных кг. Аналогично, молярная магнитная восприимчивость определяется как восприимчивость одного моля вещества и измеряется в обратных молях.
- напряженность магнитного поля. Иногда вводят понятие удельной магнитной восприимчивости, равной восприимчивости единицы массы вещества. В СИ удельная восприимчивость измеряется в обратных кг. Аналогично, молярная магнитная восприимчивость определяется как восприимчивость одного моля вещества и измеряется в обратных молях. . Также указываются направления m:n:p=
. Также указываются направления m:n:p=  :
:  :
:  . Числа [m n p]- индексы направлений. Если
. Числа [m n p]- индексы направлений. Если  , то направление противоположно оси. Если необходимо задать индексы в плоскости, то смотрят на отрезки, отсекаемые плоскостью на осях.
, то направление противоположно оси. Если необходимо задать индексы в плоскости, то смотрят на отрезки, отсекаемые плоскостью на осях. :
:  :
:  . h,k,l- индексы Миллера. Если плоскость параллельна оси и отсекаемый ею отрезок бесконечно велик, то составляющий индекс Миллера=0.Дефектами КР наз-ся отклонения от упорядоченного расположения частиц в узлах решетки. Делятся на макроскопические, возникающие в процессе образования и роста К (поры, инородные включения) и микроскопические, обусловленные микроскопическими отклонениями от периодичности. Микродефекты делятся на точечные, линейные, поверхностные, объемные. Точечные: 1 Вакансия- отсутствие атома в узле КР. 2 Междоузельный атом- атом, внедрившийся в междоузельное пространство. 3 Примесный атом – атом примеси (атом другого сорта). Точечные дефекты нарушают только ближний порядок, не затрагивая дальний. В отличие от них дислокации нарушают дальний порядок- правильное чередование а
. h,k,l- индексы Миллера. Если плоскость параллельна оси и отсекаемый ею отрезок бесконечно велик, то составляющий индекс Миллера=0.Дефектами КР наз-ся отклонения от упорядоченного расположения частиц в узлах решетки. Делятся на макроскопические, возникающие в процессе образования и роста К (поры, инородные включения) и микроскопические, обусловленные микроскопическими отклонениями от периодичности. Микродефекты делятся на точечные, линейные, поверхностные, объемные. Точечные: 1 Вакансия- отсутствие атома в узле КР. 2 Междоузельный атом- атом, внедрившийся в междоузельное пространство. 3 Примесный атом – атом примеси (атом другого сорта). Точечные дефекты нарушают только ближний порядок, не затрагивая дальний. В отличие от них дислокации нарушают дальний порядок- правильное чередование а 


