
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимодействие квантовой системы с излучением.Содержание книги
Поиск на нашем сайте
Квантовое э/м поле. Прост-во сост-й э/м поля. Уравнения Максвалла в гамильтоновой форме. Исследуем систему фотонов (квантов э/м поля) с помощью метода вторичного квантования. В представл-и этого метода все операторы выраж-ся ч/з операторы рождения и уничтожения частиц в одночастич. сост-х с числом степеней свободы только одной частицы, а сост-е всей системы описывается ф-ми, зависящими от чисел, указыв-х число частиц в каждом одночастич. сост-и. Э/м поле в классич. электродинамике опис-ся с помощью плотности ф-и Лагранжа:
-соответственно волновой вектор фотона, объем, в кот. заключено э/м поле, вектор поляризации фотона. В сост-х с опред. числом частиц
Два собственных значения +1 и –1 оператора проекции спина частицы на направление импульса наз. спиральностью частицы. в сост-х с определенной спиральностью каждому значению импульса соответствует только одно спиновое сост-е. При положительной спиральности напр-е импульса и направление спина параллельны. При отриц. спиральности антипар-ны. Такие сост-я м/т реализовать отлько частица с нулевой массой покоя и двигающаяся со скоростью света (фотон). Квантовая система в поле э/м волны. Дипольное приближение. Вероятность перехода. Матричный элемент оператора дипольного момента. Правила отбора. Спектральные серии. Взаимодействие бесспиновой частицы массы m и заряда е, входящей в состав атома (молекулы), с э/м полем, описываемым векторным потенциалом
Положим
(е-определяет направление поляризации фотона), наз. дипольным электрическим моментом перехода l®f. Э/м излучение, обусловленное отличным от нуля матричным элементом (10) наз-ся дипольным э/м излучением. Мультиплетность линий излучения опред-ся мультиплетностью энергетических уровней атома. Чтобы опред-ть мультиплетность линий изл-я по мультиплет-ти энергет. уровней, необходимо знать правила отбора для квантовых чисел l (орбитального), s (спинового), J (полного момента атома) при оптических переходах (переходах валентного (внешнего электрона)). Если взаимод-е м/у различными электронами не очнь велико, то происходят лишь такие переходы, пр кот. скачок совершается лишь одним е-, правило отбора для кот. есть Dl=±1, (11). Из этой фор-лы следует, что кв. число полного момента L м/т изменятся на ±1, т. е. DL=±1, (12). Лишь в том случае, когда взаимод-е м/у е- интенсивно, два и больше е- м/т совершить переход DL=0 (12а). Для спина DS=0, (13). Если скомбинировать (12,12а,13) DJ=0, (14), с доп. правилом, что невозможен переход из сост-я J=0 в сост-е J=0. Если рассм-ть спектр водорода, то м/о выделить след. спектр. серии: серия Лаймана (переход с основного ур-я на выше лежащие), серия Бальмера (со второго ур-я на выше лежащие) и т. д. Используя правила отбора для l и условные обозначения сост-й е-, переходы приводящие к возникновению серии Лаймана и/т вид: np®1s, n=2,3,…, серии Бальмера ns®2p, n=3,4,… Cост-е 1s наз-ся основным Н2. Спектр поглощения д/н сост-ть из линий соотвеств-х переходам 1s®np, n=2,3,… Cпектры испускания щелочных металлов также сост-т из неск-х серий: главной, диффузной, основной и резкой, кот. явл-ся наиболее четкими. Главная серия набл-ся и при поглощении, резкая и диффузная сост-т соотв-но из резких и расплывчатых линий. Основная (серия Бальмера) сходна с серией Н2. Для l справедливы те же правила отбора, что и в случае Н2. Щелочно-земельные и/т 2 оптических (валентных е-). Для спинового квантового числа вып-ся след. правило отбора: s=0,1. Если s=0, то ур-ни синглетны, если s=1, то уровни триплетны. Спонтанными переходами наз-ся самопроизвольные переходы атома из возбужд. сост-я в более низкое энергетич. сост-е. Время t за кот. число атомов нах-ся на данном энергет. уровне уменьшится в е раз наз-ся временем жизни возбужд. сост-я. Под естеств. спектральной шириной понимают величину
Атом во внешнем поле В отсутствии магнитного поля векторы орбитального В слабом поле энергия взаимодействия орбитального и спинового моментов между собой (энергия спин-орбитального взаимодействия
( Другими словами, в слабом поле зеемановское расщепление (уровней, линий) значительно меньше естественного мультиплетного расщепления. В слабом магнитном поле вектор В противоположном случае сильного поля
Под промежуточными магнитными полями подразумеваются поля, напряженность которых лежит между ее значениями для сильного и слабого полей. В промежуточных полях не сохраняется ни один из моментов количества движения Слабое поле. В слабом поле энергия атома
где фактор Ланде
Для Для Аналогично определяются орбитальное
Из формулы (3) видно, что при помещении атома в магнитное поле происходит расщепление уровня энергии на
где
Зеемановское расщепление определяется формулой:
или, в волновых числах
Спектральные переходы возможны только между подуровнями, магнитные квантовые числа, которые подчиняются правилам отбора
Различают простой и сложный эффекты Зеемана. Простой эффект может быть получен при
или
т.е. для синглетных линий Поляризация компонент зеемановского расщепления определяется правилами отбора по Сильное поле. Эффект Зеемана в сильном поле называется также эффектом Пашена-Бака. В сильном поле при
Зеемановское расщепление
так как Или, в волновых числах
Результат совпадает с полученным выше для простого эффекта Зеемана. Более точный расчет требует учета остаточного
Химическая связь, молекулы При исследовании движ-я электронов координаты ядер изменяются настолько медленно, что их м\о считать неизменными (адиабатическое приближение). Чтобы понять основные идеи метода адиабатического приближения, рассмотрим систему, состоящую из некоторого числа электронов с массой
где
Адиабатическое приближение основывается на предположении, что оператор кинетической энергии
Тогда в нулевом приближении, когда масса тяжелых частиц рассматривается бесконечно большой, задача отыскания стационарных состояний системы сводится к решению уравнения Шредингера
для фиксированных значений координат R тяжелых частиц. Индекс Химические связи. Ионная связь (гетерополярной). Валентность химического элемента определяется числом электронов, которые нужно прибавить или отнять к его электронной оболочке, что бы получить ион, с электронной оболочкой ближайшего к нему инертного газа. Так ион натрия Электроны в молекулах с ионной связью разделены на группы, каждая из которых все время находится у своего ядра. Кулоновское притяжение разноименно заряженных ионов играет решающую роль в механизме ионной связи, но для того, что бы молекула была устойчивой необходимо добавить силы отталкивания, действующие на малых расстояниях. Ковалентная связь ( гомеополярной). При сближении атомов на достаточное расстояние происходит обобществление валентных электронов. Квантовый эффект неразличимости тождественных частиц приводит к специфическому эффекту - обменному взаимодействию. Электрон каждого из атомов молекулы некоторое время проводит около другого атома, осуществляя, таким образом, связь между ними. Ковалентная связь обладает свойством насыщения. Простейшей молекулой с гомеополярной связью явл-ся молекула водорода. Обозначим:
Потенц. энергия такой системы: U =
|
||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.65.133 (0.014 с.) |

 где А –вектор. потенциал, ч/з кот. при усл-и div A=0 выр-ся напряженнность эл. поля Е и магнит. В.
где А –вектор. потенциал, ч/з кот. при усл-и div A=0 выр-ся напряженнность эл. поля Е и магнит. В.  Учитывая, что
Учитывая, что  и решая ур-е Лагранжа
и решая ур-е Лагранжа  Получаем из (1) первое ур-е Максвелла
Получаем из (1) первое ур-е Максвелла  Три других ур-я следуют из (2)
Три других ур-я следуют из (2)  Из (2) и (4) получаем ур-е для вектор. потенциала:
Из (2) и (4) получаем ур-е для вектор. потенциала:  Выр-е для обобщенного импульса и/т вид:
Выр-е для обобщенного импульса и/т вид:  Ф-я Гамильтона, выр-ся ч/з вектор. потенциал и обобщ. импульс и/т вид:
Ф-я Гамильтона, выр-ся ч/з вектор. потенциал и обобщ. импульс и/т вид:  где
где  -операторы уничтожения и рождения фотона. Переходя в (2) к операторам вектор. пот-ла и обобщ. имп., выраженные в свою очередь ч/з
-операторы уничтожения и рождения фотона. Переходя в (2) к операторам вектор. пот-ла и обобщ. имп., выраженные в свою очередь ч/з 
 .где
.где 
 энергия и импульс опред-ся выр-ем:
энергия и импульс опред-ся выр-ем:  Т. об. квантование э/м поля соответствует введению элементарных возбуждений фотонов, имеющих энергию
Т. об. квантование э/м поля соответствует введению элементарных возбуждений фотонов, имеющих энергию  и импульс
и импульс  , поляризацию
, поляризацию  переход от классич. величин
переход от классич. величин  , описывающих э/м поле к операторам наз. квантованием (второичным квантованием) поля. Спин и спиральность фотона. Состояние фотонов опред-ся энергией
, описывающих э/м поле к операторам наз. квантованием (второичным квантованием) поля. Спин и спиральность фотона. Состояние фотонов опред-ся энергией  , импульсом
, импульсом  перпендикулярными д/д и вектору Q, а также с помощью спинового момента фотона. Понятие спинового момента фотона вводится как наименьшего из всех возможных значений его мом. импульса. Проекции оператора спинового момента импульса опред-ся тремя матрицами со спином S=1
перпендикулярными д/д и вектору Q, а также с помощью спинового момента фотона. Понятие спинового момента фотона вводится как наименьшего из всех возможных значений его мом. импульса. Проекции оператора спинового момента импульса опред-ся тремя матрицами со спином S=1
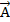 , опред-ся оператором
, опред-ся оператором 
 -оператор импульса. Вероятности перехода м/о представить в виде ряда по оператору взаимодейст-вия W(t) при вычислении методом теории возмущения с порядком малости
-оператор импульса. Вероятности перехода м/о представить в виде ряда по оператору взаимодейст-вия W(t) при вычислении методом теории возмущения с порядком малости  (постоянная тонкой структуры). В первом приближении оставим только первый член
(постоянная тонкой структуры). В первом приближении оставим только первый член  Без учета взаимодействия (6) гамильтониан полной системы представляет собой сумму гамильтонианов атома Нa и э/м поля НF. Предположим, что решение ур-я Шредингера для атома и/т вид: (Нa-Ее)jе=0,(7)
Без учета взаимодействия (6) гамильтониан полной системы представляет собой сумму гамильтонианов атома Нa и э/м поля НF. Предположим, что решение ур-я Шредингера для атома и/т вид: (Нa-Ее)jе=0,(7) с собственными ф-ми
с собственными ф-ми  -фотонов. Здесь как и раньше
-фотонов. Здесь как и раньше  - операторы рождения и уничтожения фотонов, волновой вектор фотонов. Матричный элемент оператора импульса обозначим
- операторы рождения и уничтожения фотонов, волновой вектор фотонов. Матричный элемент оператора импульса обозначим  собственные ф-и полной системы до и после взаимодействия. Разлагая в матричном элементе экспоненту в ряд:
собственные ф-и полной системы до и после взаимодействия. Разлагая в матричном элементе экспоненту в ряд:  м/о учесть первый член ряда, т. е. положить
м/о учесть первый член ряда, т. е. положить  .Такое упрощение наз. длинноволновым приближением (дипольным?). Если перейти от матричного элемента оператора импульса к матричному элементу от оператора координаты
.Такое упрощение наз. длинноволновым приближением (дипольным?). Если перейти от матричного элемента оператора импульса к матричному элементу от оператора координаты 

 характер-ю вел-ну разброса энергии Е в данном сост-и. э/м вакуум. Опыт Лэмба и Резерфорда. Лэмбовский сдвиг. Ур-и энергии атома Н2 зависят от главного квант. числа n и полного квант. числа J. Поэтому 2 различных сост-я с одинаковыми числами n и J согласно теории Дирака д/ы обладать одинаковой энергией, причем их совпадение д/б точным. Лэмб и Резерфорд воспользовались тем, что уровень
характер-ю вел-ну разброса энергии Е в данном сост-и. э/м вакуум. Опыт Лэмба и Резерфорда. Лэмбовский сдвиг. Ур-и энергии атома Н2 зависят от главного квант. числа n и полного квант. числа J. Поэтому 2 различных сост-я с одинаковыми числами n и J согласно теории Дирака д/ы обладать одинаковой энергией, причем их совпадение д/б точным. Лэмб и Резерфорд воспользовались тем, что уровень  явл-ся метастабильным, а уровень
явл-ся метастабильным, а уровень  нестабильным. Переход из
нестабильным. Переход из 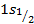 запрещен правилом отбора Dl=+1, поск-ку при этом переходе Dl=0. Переход из
запрещен правилом отбора Dl=+1, поск-ку при этом переходе Dl=0. Переход из 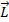 и спинового
и спинового  моментов количества движения прецессируют вокруг полного момента количества движения
моментов количества движения прецессируют вокруг полного момента количества движения  . При помещении атома в постоянное однородное магнитное поле характер взаимодействия атома с полем будет различным в зависимости от того, является ли магнитное поле «слабым» или «сильным».
. При помещении атома в постоянное однородное магнитное поле характер взаимодействия атома с полем будет различным в зависимости от того, является ли магнитное поле «слабым» или «сильным». ) значительно больше энергии их взаимодействия с магнитным полем, имеющий порядок величины
) значительно больше энергии их взаимодействия с магнитным полем, имеющий порядок величины 
 магнетон Бора,
магнетон Бора,  напряженность магнитного поля).
напряженность магнитного поля). . Его проекция на направление магнитного поля сохраняется. Частота этой прецессии значительно меньше, чем частота прецессии
. Его проекция на направление магнитного поля сохраняется. Частота этой прецессии значительно меньше, чем частота прецессии  (2)
(2) связь разрывается и векторы
связь разрывается и векторы 
 изменяется на величину, равную энергии взаимодействия полного магнитного момента атома
изменяется на величину, равную энергии взаимодействия полного магнитного момента атома 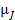 с полем
с полем  .
. (3)
(3) (4)
(4) квантовые числа, соответственно орбитальное, спиновое и полного момента количества движения,
квантовые числа, соответственно орбитальное, спиновое и полного момента количества движения, магнитное квантовое число.
магнитное квантовое число. всего
всего  значений. (5)
значений. (5) (
( состояния)
состояния)  .
.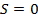 (синглеты, состояние определяется только орбитальным моментом)
(синглеты, состояние определяется только орбитальным моментом)  .
. и спиновое
и спиновое  магнитные квантовые числа.
магнитные квантовые числа.
 значений (6)
значений (6)
 значений (7)
значений (7)
 энергия уровней атома при
энергия уровней атома при 
 - дополнительные энергии, приобретаемые атомом в магнитном поле.
- дополнительные энергии, приобретаемые атомом в магнитном поле. ,
,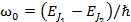 - частота излучения в отсутствие магнитного поля.
- частота излучения в отсутствие магнитного поля.
 , (8)
, (8)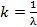
 ,
,

 .
. 0,
0,  (11)
(11) ,
, 

 в магнитном поле наблюдается не более трех компонент.
в магнитном поле наблюдается не более трех компонент. . Для линии, у которых
. Для линии, у которых  в продольном поле наблюдается круговая поляризация (
в продольном поле наблюдается круговая поляризация ( компоненты), линии с
компоненты), линии с  линейно поляризованы вдоль поля (
линейно поляризованы вдоль поля ( компоненты). Отсюда ясно, что при изменении направления наблюдения будет изменяться и поляризация зеемановских компонент.
компоненты). Отсюда ясно, что при изменении направления наблюдения будет изменяться и поляризация зеемановских компонент.
 (12)
(12) и
и  - орбитальный и спиновой магнитные моменты атома,
- орбитальный и спиновой магнитные моменты атома,  - энергия центра тяжести мультиплета. Частоты, излучаемые атомом в магнитном поле, определяются из уравнения
- энергия центра тяжести мультиплета. Частоты, излучаемые атомом в магнитном поле, определяются из уравнения .
. 0,
0, 



 и атомных ядер с массой
и атомных ядер с массой  . Совокупность координат всех электронов относительно центра инерции всей системы обозначим буквой
. Совокупность координат всех электронов относительно центра инерции всей системы обозначим буквой  , а совокупность координат ядер — буквой
, а совокупность координат ядер — буквой  . Оператор Гамильтона, определяющий внутреннее состояние, системы, можно записать в виде
. Оператор Гамильтона, определяющий внутреннее состояние, системы, можно записать в виде


 —оператор кинетической энергии электронов (легкие частицы);
—оператор кинетической энергии электронов (легкие частицы);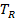 — оператор кинетической энергии ядер (тяжелые частицы;
— оператор кинетической энергии ядер (тяжелые частицы;  — оператор потенциальной энергии взаимодействия между всеми частицами.
— оператор потенциальной энергии взаимодействия между всеми частицами.

 определяет совокупность квантовых чисел, характеризующих- стационарное состояние. В каждом таком состоянии, соответствующем определенному значению n, энергия системы
определяет совокупность квантовых чисел, характеризующих- стационарное состояние. В каждом таком состоянии, соответствующем определенному значению n, энергия системы  и волновые функции
и волновые функции  зависят от координат тяжелых частиц R как от параметров. Таким образом, функции
зависят от координат тяжелых частиц R как от параметров. Таким образом, функции  и ион хлора
и ион хлора  можно рассматривать как заряженные атомы инертных газов
можно рассматривать как заряженные атомы инертных газов  и
и  соответственно. Их электронные оболочки при этом полностью достроены. Разноименно заряженные ионы, притягиваясь, образуют молекулу
соответственно. Их электронные оболочки при этом полностью достроены. Разноименно заряженные ионы, притягиваясь, образуют молекулу  . Образование разноименно заряженных ионов объясняется переходом электрона от натрия к хлору.
. Образование разноименно заряженных ионов объясняется переходом электрона от натрия к хлору.
 - расстояние между ядрами,
- расстояние между ядрами, — расстояние между электронами,
— расстояние между электронами, - расстояние между ядром А и электроном 1,
- расстояние между ядром А и электроном 1, - расстояние между ядром В и электроном 2,
- расстояние между ядром В и электроном 2, - расстояние между ядром А и электроном 2,
- расстояние между ядром А и электроном 2, - расстояние между ядром В и электроном 1,
- расстояние между ядром В и электроном 1, В первом приближ-и (ядра считаем неподвижными) ур-е Шредингера имеет вид
В первом приближ-и (ядра считаем неподвижными) ур-е Шредингера имеет вид  = 0.Здесь
= 0.Здесь  - оператор Лапласа, содержащий координаты одного электрона, а
- оператор Лапласа, содержащий координаты одного электрона, а  - оператор Лапласа, содержащий координаты другого электрона. Получающиеся из ур-я Шредингера собственные знач-я энергии оказ-ся зависящими от расстояния м\у ядрами R, т.е. E = E(R), причем в случаях параллельной и антипараллельной ориентации спинов электронов хар-р этой завис-ти существенно различен (см. рис.). Образование молекулы возможно лишь при сближении атомов с антипараллельными спинами. Асимптотическое знач-е
- оператор Лапласа, содержащий координаты другого электрона. Получающиеся из ур-я Шредингера собственные знач-я энергии оказ-ся зависящими от расстояния м\у ядрами R, т.е. E = E(R), причем в случаях параллельной и антипараллельной ориентации спинов электронов хар-р этой завис-ти существенно различен (см. рис.). Образование молекулы возможно лишь при сближении атомов с антипараллельными спинами. Асимптотическое знач-е  , к к-рому стремиться энергия молекулы при
, к к-рому стремиться энергия молекулы при 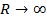 для обеих изображенных на рис.кривых, одинаково и равно сумме энергий изолированных атомов.
для обеих изображенных на рис.кривых, одинаково и равно сумме энергий изолированных атомов.


