
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоские электромагнитные волны в прозрачном веществе.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Опыты по обнаружению электромагнитных волн указывают на то, что эти волны переносят энергию. Объемная плотность энергии W электромагнитной волны складывается из объемных плотностей электрического WE и магнитного WH полей:
В данной точке пространства векторы Поэтому выражение (3.1) можно представить:
Умножив плотность энергии на скорость электромагнитных волн Векторы
вектор Вектор Интенсивность света (плотность светового потока усредненная по времени) определяется модулем среднего значения плотности потока электромагнитной энергии, т. е. средним значением вектора Умова-Пойнтинга:
В случае синусоидальной монохроматической плоской (когда плоскости колебаний векторов Е и Н не меняются со временем) электромагнитной волны, распространяющейся в направлении х:
для интенсивности получается:
Если электромагнитные волны поглощаются или отражаются телами (эти явления подтверждены опытами Г. Герца), то из теории Максвелла следует, что электромагнитные волны должны оказывать на тела давление. Давление электромагнитных волн объясняется тем, что под действием электрического поля волны заряженные частицы вещества начинают упорядоченно двигаться и подвергаются со стороны магнитного поля волны действию сил Лоренца. Однако значение этого давления ничтожно мало. Существование давления электромагнитных воли приводит к выводу о том, что электромагнитному полю присущ механический импульс. Импульс электромагнитного поля где W — энергия электромагнитного поля. Выражая импульс как р=тс (поле в вакууме распространяется со скоростью с), получим р=тс= W/c. Интенсивность света (плотность светового потока усредненная по времени) определяется Давление света Если электромагнитные волны поглощаются или отражаются телами (эти явления подтверждены опытами Герца), то из теории Максвелла следует, что электромагнитные волны должны оказывать на тела давление. Давление ЭМВ объясняется тем, что под действием электрического поля волны заряженные частицы вещества начинают упорядоченно двигаться и подвергаются со стороны магнитного поля действию силы. Однако, значение этого давления ничтожно мало. Впервые световое давление в 1899 г. измерил русский физик П. Н. Лебедев. Он подвесил на тонкой нити две пары крылышек: поверхность у одной из них была зачерненной, а у другой — зеркальной (рис. 3). Свет практически полностью отражался от зеркальной поверхности, и его давление на зеркальное крылышко было вдвое большим (R = 1), чем на зачерненное (R = 0). Создавался момент сил, поворачивающий устройство. По углу поворота можно было судить о силе, действовавшей на крылышки, а значит, измерить световое давление. Согласно теории Максвелла, причиной возникновения электромагнитных волн является ускоренное движение электрических зарядов. Колебания электронов под воздействием переменного электрического напряжения в антенне радиопередатчика создают электромагнитные волны, распространяющиеся в земной атмосфере. Все другие типы электромагнитных волн также возникают в результате различных видов ускоренного движения электрических зарядов. По первоначальной теории Максвелла для учёта влияния вещества на электромагнитные процессы необходимо было принимать во внимание три характеристики вещества: диэлектрическую проницаемость ε, магнитную проницаемость μ и проводимость σ вещества. Диэлектрическая и магнитная проницаемости определяют скорость v распространения электромагнитных волн в данной среде:
а проводимость σ определяет поглощение волны.
Явление интерференции.
Метод Юнга. (рис. 3,4.) Роль вторичных когерентных источников S1 и S2 играют две узкие щели, освещаемые одним источником малого углового размера, а в более поздних опытах свет от источника пропускался через узкую щель S, равноудаленную от двух других щелей. Так как волны, исходящие из S1 и S2, получены разбиением одного и того же волнового фронта, исходящего из S, то они являются когерентными, и в области перекрытия этих световых пучков наблюдается интерференционная картина(на рис. 3,4. эта область окрашена). Юнгу принадлежит первое наблюдение интерференции). Метод Френеля. Свет от источника S падает расходящимся пучком на два плоских
Интерферометр Майкельсона. Примером двулучевого интерферометра(все интерферометры отличаются лишь конструкционно, так как основаны на одном и том же принципе) может служить интерферометр Майкельсона. Его схема на рис. Монохроматический свет от источника S падает под углом 450 на плоскопараллельную пластинку Р1. Сторона пластинки, удаленная от S, посеребренная и полупрозрачная, разделяет луч на две части: луч 1 (отражается от посеребренного слоя) и луч 2 (проходит через него). Луч 1 отражается от зеркала М1 и, возвращаясь обратно, вновь проходит через пластинку Р1 (луч 1). Луч 2 идет к зеркалу М2, отражается от него, возвращается обратно и отражается от пластинки Р1 (луч 2¢). Так как первый из лучей проходит пластинку Р1 дважды, то для компенсации возникающей разности хода на пути второго луча ставится пластинка Р2 (точно такая же, как и Р1, только не покрытая слоем серебра). Лучи 1¢ и 2¢ когерентны: следовательно, будет наблюдаться интерференция, соответствующая интерференции в воздушном слое, образованном зеркалом М1 и мнимым изображением М2¢ зеркала М2 в пластинке Р2. Оптическая разность хода D = 2(ОС – ОВ) = 2l (l – расстояние между М1 и М2¢). Если зеркало М2 расположено так, что М1 и М2¢ параллельны, то наблюдаются полосы равного наклона (локализованы в фокальной плоскости линзы и имеют форму концентрических колец), а если М1 и М2¢ образуют воздушный клин, то полосы равной толщины (локализованы в плоскости клина М1М2¢ и представляют собой параллельные линии). По незначительному смещению интерференционной картины можно судить о малом перемещении одного из зеркал и использовать интерферометр Майкельсона для точного (» 10-7 м) измерения длин(длины тел, длин волн и т.д.). Когерентность – это согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов, проявляющееся при их сложении. Время и длина когерентности. Реальная волна, излучаемая в течение ограниченного промежутка времени и охватывающая ограниченную область пространства, не является монохроматической. Спектр ее циклических частот имеет конечную ширину Dw, т.е. включает циклические частоты от w - Степень когерентности. Частично когерентный свет, общая интенсивность которого равна I, можно рассматривать как совокупность двух составляющих – когерентной с интенсивностью gI, где g - степень когерентности света, и некогерентной с интенсивностью (1 - g)I. При наложении частично когерентных волн интерферируют только их когерентные составляющие. Некогерентные составляющие создают равномерно освещенный фон интерференционной картины. Поэтому по мере уменьшения степени когерентности света видимость интерференционных полос V уменьшается: Многолучевая интерференция. Для осуществления интерференции многих световых волн с близкими или равными амплитудами применяют специальные интерференционные приборы – дифракционную решетку, эталон Фабри – Перо и др. Амплитуду А результирующих колебаний и их интенсивность I = А2 в произвольной точке М интерференционной картины можно найти, воспользовавшись методом векторных диаграмм для сложения одинаково направленных колебаний. На рис. 1. показана векторная диаграмма сложения колебаний при интерференции N волн, возбуждающих в рассматриваемой точке М одинаково направленные когерентные колебания с равными амплитудами Аi = А1 и не зависящим от i сдвигом фаз между (i + 1)- м и i – м колебаниями: Фi +1(t) – Фi(t) = Dj0. Амплитуда результирующих колебаний А = 2*OO1 Интерферометр Фабри – Перо. Рассмотрим его в качестве примера многолучевого интерферометра.(рис.). Он состоит из двух стеклянных(или кварцевых) пластинок: Р1 и Р2. Их внутренние поверхности плоские, параллельны между собой и на них нанесенные зеркальные покрытия с высоким коэффициентом отражения(»85 – 98%). Для устранения света, отраженного внешними поверхностями, их изготовляют так, что они составляют небольшой угол с внутренними поверхностями. Пластинки могут передвигаться в параллельном друг относительно друга направлении. Параллельный пучок света(на рис. 1). Показан ход одного из лучей) в результате многократного отражения от зеркал образует большое число параллельных когерентных пучков с постоянной разностью хода
Явление дифракции
Рис.1. Вид дифракционной картины от плоскости Согласно принципу Гюйгенсу каждую точку волновой поверхности следует рассматривать как источник элементарных сферических волн, огибающая их поверхность служит новой волновой поверхностью (рис.2).
Волновая поверхность Σ является источником вторичных сферических волн (рис.3). Каждая точка поверхности Σ эмитирует световые волны в различных направлениях. Выберем те лучи, которые собираются в точке экрана. Эти лучи когерентны, т.е. имеют одинаковую частоту, постоянную разность фаз, следовательно, могут интерферировать. Если лучи приходят в точку Р в фазе, то происходит усиление света и мы наблюдаем световую полосу. В некоторую точку P 1 лучи приходят в противофазе и происходит взаимное ослабление света. Тогда в точке Р 1 мы наблюдаем тёмную полосу и т.д. Аналогично можно объяснить явление дифракции на щели на круглом отверстии и на других преградах.
|
||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.238.67 (0.012 с.) |

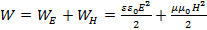 (3.1)
(3.1) и
и  изменяются в одинаковой фазе (это справедливо только для непроводящей среды). Поэтому соотношение
изменяются в одинаковой фазе (это справедливо только для непроводящей среды). Поэтому соотношение  между амплитудными значениями E и H справедливо и для их мгновенных значений. Отсюда следует, что плотность энергии электрического и магнитного полей в каждый момент времени одинакова: WE=WH
между амплитудными значениями E и H справедливо и для их мгновенных значений. Отсюда следует, что плотность энергии электрического и магнитного полей в каждый момент времени одинакова: WE=WH . (3.2)
. (3.2) , получим плотность потока энергии: S=wV=EH
, получим плотность потока энергии: S=wV=EH совпадает с направлением переноса энергии, модуль этого вектора равен EH (т.к. sina=1). Следовательно, вектор плотности потока энергии можно представить как векторное произведение
совпадает с направлением переноса энергии, модуль этого вектора равен EH (т.к. sina=1). Следовательно, вектор плотности потока энергии можно представить как векторное произведение  (3.3)
(3.3) называется вектором Умова-Пойнтинга.
называется вектором Умова-Пойнтинга.




 Интерференция волн – сложение когерентных волн, при котором в разных точках пространства получается усиление или ослабление амплитуды результирующей волны.
Интерференция волн – сложение когерентных волн, при котором в разных точках пространства получается усиление или ослабление амплитуды результирующей волны. зеркала А1О и А2О, расположенных друг относительно друга под углом, лишь немного отличающемся от 1800(угол j мал). Учитывая правила построения изображения в плоских зеркалах, можно показать, что и источник и его изображения S1 и S2 (угловое расстояние между ними равно 2j) лежат на одной и той же окружности радиуса r с центром в О(точка соприкосновения зеркал). Световые пучки, отражаясь от зеркал, образуют два мнимых изображения источника S1 и S2, которые действуют как когерентные источники(получены разбиением одного и того же волнового фронта, исходящего из S). Интерференционная картина наблюдается в области взаимного перекрытия отраженных пучков(экран Э защищен от прямого поподания света заслонкой З).
зеркала А1О и А2О, расположенных друг относительно друга под углом, лишь немного отличающемся от 1800(угол j мал). Учитывая правила построения изображения в плоских зеркалах, можно показать, что и источник и его изображения S1 и S2 (угловое расстояние между ними равно 2j) лежат на одной и той же окружности радиуса r с центром в О(точка соприкосновения зеркал). Световые пучки, отражаясь от зеркал, образуют два мнимых изображения источника S1 и S2, которые действуют как когерентные источники(получены разбиением одного и того же волнового фронта, исходящего из S). Интерференционная картина наблюдается в области взаимного перекрытия отраженных пучков(экран Э защищен от прямого поподания света заслонкой З). Полосы равной толщины и равного наклона. Рассматривая интерференцию света в тонких пленках, различают интерференционные полосы равного наклона и равной толщины. Полосы равного наклона наблюдаются в тех случаях, когда на плоскопараллельную тонкую пленку падает под разными углами i расходящийся (или сходящийся) пучок света. Таковы, например, условия освещения пленки протяженным источником или рассеянным солнечным светом. Так как d и n всюду одинаковы, то оптическая разность хода интерферирующих волн изменяется вдоль поверхности пленки только из-за изменения угла падения света i. Условия интерференции для всех лучей, падающих на поверхность пленки и отражающихся от нее под одним и тем же углом, одинаковы. Соответственно в этом случае интерференционная картина называется полосами равного наклона. Полосы равного наклона наблюдаются на экране Э, установленном в фокальной плоскости собирающей линзы Л.(рис. 1.) В отсутствие линзы интерференционную картину можно было бы наблюдать только на бесконечности – в месте пересечения пар параллельных лучей 1¢1¢¢, 2¢2¢¢ и т.д. Поэтому говорят, что полосы равного наклона локализованы в бесконечности. Для их визуального наблюдения нужно аккомодировать глаз на бесконечность.
Полосы равной толщины и равного наклона. Рассматривая интерференцию света в тонких пленках, различают интерференционные полосы равного наклона и равной толщины. Полосы равного наклона наблюдаются в тех случаях, когда на плоскопараллельную тонкую пленку падает под разными углами i расходящийся (или сходящийся) пучок света. Таковы, например, условия освещения пленки протяженным источником или рассеянным солнечным светом. Так как d и n всюду одинаковы, то оптическая разность хода интерферирующих волн изменяется вдоль поверхности пленки только из-за изменения угла падения света i. Условия интерференции для всех лучей, падающих на поверхность пленки и отражающихся от нее под одним и тем же углом, одинаковы. Соответственно в этом случае интерференционная картина называется полосами равного наклона. Полосы равного наклона наблюдаются на экране Э, установленном в фокальной плоскости собирающей линзы Л.(рис. 1.) В отсутствие линзы интерференционную картину можно было бы наблюдать только на бесконечности – в месте пересечения пар параллельных лучей 1¢1¢¢, 2¢2¢¢ и т.д. Поэтому говорят, что полосы равного наклона локализованы в бесконечности. Для их визуального наблюдения нужно аккомодировать глаз на бесконечность. Полосы равной толщины наблюдаются при отражениипараллельного или почти параллельного пучка лучей света(i = const) от тонкой прозрачной пленки, толщина d которой неодинакова в разных местах. Оптическая разность хода интерферирующих волн изменяется при переходе от одних точек на поверхности пленки к другим в соответствии с изменением толщины d, так что условия интерференции одинаковы в точках, соответствующих одинаковым значениям d. Поэтому рассматриваемая интерференционная картина и называется полосами равной толщины. Полосы равной толщины локализованы вблизи поверхности пленки, т.е. для их наблюдения нужно аккомодировать глаз практически на поверхность самой пленки.
Полосы равной толщины наблюдаются при отражениипараллельного или почти параллельного пучка лучей света(i = const) от тонкой прозрачной пленки, толщина d которой неодинакова в разных местах. Оптическая разность хода интерферирующих волн изменяется при переходе от одних точек на поверхности пленки к другим в соответствии с изменением толщины d, так что условия интерференции одинаковы в точках, соответствующих одинаковым значениям d. Поэтому рассматриваемая интерференционная картина и называется полосами равной толщины. Полосы равной толщины локализованы вблизи поверхности пленки, т.е. для их наблюдения нужно аккомодировать глаз практически на поверхность самой пленки. доw +
доw +  как монохроматическую волну с циклической частотой w. Величина tког называется временем когерентности немонохроматической волны. За промежуток времени, равныйtког, разность фаз колебаний, соответствующих волнам с частотами w -
как монохроматическую волну с циклической частотой w. Величина tког называется временем когерентности немонохроматической волны. За промежуток времени, равныйtког, разность фаз колебаний, соответствующих волнам с частотами w -  . Величина lког называется длиной когерентности или длиной гармонического цуга.
. Величина lког называется длиной когерентности или длиной гармонического цуга. g. Если интенсивности частично когерентных волн одинаковы, то V = g.
g. Если интенсивности частично когерентных волн одинаковы, то V = g. , где a = 2p - NDj0 и OO1 =
, где a = 2p - NDj0 и OO1 =  Поэтому А = А1
Поэтому А = А1  и I = I1
и I = I1  . Где I1 = A12 – интенсивность колебаний, возбуждаемых в точке М каждой из N интерферирующих волн порознь.
. Где I1 = A12 – интенсивность колебаний, возбуждаемых в точке М каждой из N интерферирующих волн порознь. между соседними пучками, но различной интенсивности. В результате многолучевой интерференции в фокальной плоскости линзы возникает интерференционная картина, представляющая собой семейство кривых равного наклона – концентрические кольца с резкими интенсивными максимумами, положение которых определяется из условия D = ml (m – целое число), т.е. зависит от длины волны. Следовательно, интерферометр Фабри – Перо разлагает сложное излучение в спектр и может применяться в качестве спектрального прибора высокой разрешающей способности, которая зависит от коэффициента отражения р зеркал и от расстояния между пластинками, возрастая с их увеличением.
между соседними пучками, но различной интенсивности. В результате многолучевой интерференции в фокальной плоскости линзы возникает интерференционная картина, представляющая собой семейство кривых равного наклона – концентрические кольца с резкими интенсивными максимумами, положение которых определяется из условия D = ml (m – целое число), т.е. зависит от длины волны. Следовательно, интерферометр Фабри – Перо разлагает сложное излучение в спектр и может применяться в качестве спектрального прибора высокой разрешающей способности, которая зависит от коэффициента отражения р зеркал и от расстояния между пластинками, возрастая с их увеличением. Поместим на пути параллельного пучка света плоскость и будем наблюдать дальнейший ход спространения световых лучей на экране Е. Если бы волна представляла собой действительно пучок параллельных прямых, то тень от объекта, поставленного на пути её распространения, должна бы иметь на экране совершенно четкие контуры. Это было предсказано геометрической оптикой и подтверждено грубыми опытами. Это "явление огибания" края препятствия волной называется дифракцией и проявляется всякий раз, когда на пути распространения фронт волны тем или иным способом ограничивается. Явление дифракции, которое не могла объяснить геометрическая оптика, находится в тесной связи с явлением интерференции и может быть объяснено на основании принципа Гюйгенса.
Поместим на пути параллельного пучка света плоскость и будем наблюдать дальнейший ход спространения световых лучей на экране Е. Если бы волна представляла собой действительно пучок параллельных прямых, то тень от объекта, поставленного на пути её распространения, должна бы иметь на экране совершенно четкие контуры. Это было предсказано геометрической оптикой и подтверждено грубыми опытами. Это "явление огибания" края препятствия волной называется дифракцией и проявляется всякий раз, когда на пути распространения фронт волны тем или иным способом ограничивается. Явление дифракции, которое не могла объяснить геометрическая оптика, находится в тесной связи с явлением интерференции и может быть объяснено на основании принципа Гюйгенса. Объясним явление дифракции на краю плоскости Р, проиллюстрированное на рис.1, на основании принципа Гюйгенса.
Объясним явление дифракции на краю плоскости Р, проиллюстрированное на рис.1, на основании принципа Гюйгенса.


