Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика абсолютно твердого тела.Содержание книги
Поиск на нашем сайте
Момент силы -величина, равная векторному произведению радиус-вектора, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Момент импульса материальной точки относительно точки O определяется векторным произведением Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело:
Тензор инерции и его главные и центральные оси. Момент импульса этой точки равен по определению
Lx=Jxxwx+Jxywy+Jxzwz, Ly=Jyxwx+Jyywy+Jyzwz, Lz=Jzxwx+Jzywy+Jzzwz.
Теорема Гюйгенса. момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями
Уравнение движения и уравнение моментов.
Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело: Физический маятник. Физический маятник - осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Кинетическая энергия твердого тела. Таким образом, кинетическая энергия тела при плоском движении слагается из энергии поступательного движения со скоростью, равной скорости центра инерции, энергии вращения вокруг оси, проходящей через центр инерции тела.
Колебательное движение. Собственные одномерные колебания - система имеет всего одну степень; свобод потенциальная энергия
Кинетическая энергия системы с одной степенью свободы имеет в общем: Выражение для лагранжевой функции системы, совершающей одномерные малые колебания
Соответствующее этой функции уравнение движения Энергия системы, совершающей малые колебания Гармонические колебания. Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Вынужденные колебания совершаются под воздействием внешней периодической силы. Фигуры Лиссажу - замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях.
Вид кривой сильно зависит от соотношения Фигуры Лиссажу, где
{\displaystyle \delta ={\frac {N-1}{N}}{\frac {\pi }{2}}\ }являются полиномами Чебышёва первого рода степени Биения — явление, возникающее при наложении двух периодических колебаний, например, гармонических, близких по частоте, выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала. Частота изменения амплитуды суммарного сигнала равна разности частот исходных сигналов. Биения возникают от того, что один из двух сигналов линейно во времени отстаёт от другого по фазе, и, в те моменты, когда колебания происходят синфазно, суммарный сигнал оказывается максимален, а в те моменты, когда два сигнала оказываются в противофазе, они взаимно гасят друг друга. Эти моменты периодически сменяют друг друга по мере того, как нарастает отставание.
|
||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 265; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.135.67 (0.007 с.) |


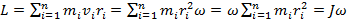

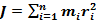 Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс материальных точек системы на квадраты их расстояний до рассматриваемой оси:
Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс материальных точек системы на квадраты их расстояний до рассматриваемой оси: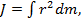 В случае непрерывного распределения масс эта сумма сводится к интегралу
В случае непрерывного распределения масс эта сумма сводится к интегралу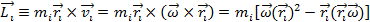
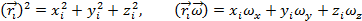
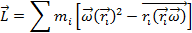
 - собственно тензор
- собственно тензор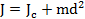

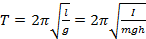 - при малых углах
- при малых углах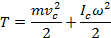
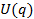 ; обобщенной координаты через
; обобщенной координаты через 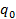 . При малых отклонениях от положения равновесия в разложении разности
. При малых отклонениях от положения равновесия в разложении разности  по степеням
по степеням 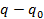 достаточно сохранить первый неисчезающий член. В общем случае таковым является член второго порядка -
достаточно сохранить первый неисчезающий член. В общем случае таковым является член второго порядка -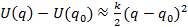 ;
;  ;
; 
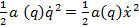 случае вид заменить функцию
случае вид заменить функцию 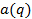 просто ее значением при
просто ее значением при 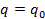 .
. .
.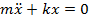 , или
, или 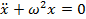 ;
; 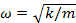 общее решение
общее решение 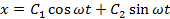 или
или  , где
, где 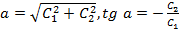 .
.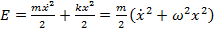 , подставив
, подставив 
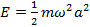 .
.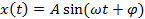
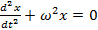 .
.
 - амплитуды колебаний,
- амплитуды колебаний,  - частоты,
- частоты, 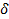 - сдвиг фаз
- сдвиг фаз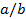 . Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид окружности (
. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид окружности ( ,
, 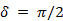 радиан) и отрезка прямой (
радиан) и отрезка прямой (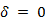 ). Ещё один пример фигуры Лиссажу — парабола (
). Ещё один пример фигуры Лиссажу — парабола ( ). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии
). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии  (
( - натуральное число) и
- натуральное число) и