
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Каноническое распределение Гиббса для системы в термостате.
распределение вероятностей состояний статистического ансамбля систем, к-рые находятся в тепловом равновесии со средой (термостатом) и могут обмениваться с ней энергией при пост. объёме и пост. числе ч-ц. Плотность распределения:
где X {\displaystyle X} Большая статистическая сумма и термодинамический потенциал. Статистическая сумма Z. Она является функцией температуры и других параметров, таких как объём. Каноническая статистическая сумма — это Смысл и значимость Статистическая сумма может быть использована для расчёта термодинамических величин, поскольку она имеет очень важный статистический смысл. Вероятность, с которой система находится в микросостоянии, равна
Идеальный газ. Модель идеального газа. 1) потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией; 2) суммарный объём молекул газа пренебрежимо мал; 3) между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги; 4) время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями. Равновесное пространственное распределение частиц идеального газа. В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана:
где n - концентрация молекул на высоте h,R - постоянная Больцмана, П - потенциальная энергия Биномиальным распределением (распределение Бернулли): в объеме
Биномиальное распределение (распределение Бернулли) – распределение вероятностей числа появлений некоторого события при повторных независимых испытания если вероятность появления этого события равна
Свойства биномиального распределения. 1) Нормировка Поскольку т.е. полная вероятность – вероятность обнаружения в малом объеме 2) Максимум вероятности. Ясно, что вероятность состояния с очень малыми Т.е. максимум вероятности должен находиться при некоторых промежуточных значениях Распределения Пуассона и Гаусса. Флуктуации. Бином Ньютона выражается формулой
Распределение Пуассона: В случа
В пределе получим
Распределение Гаусса: Прологарифмируем распределение Пуассона, получим
Уравнение состояния идеального газа (иногда уравнение Менделеева — Клапейрона или уравнение Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
Статистика идеального газа. Распределение молекул газа по скоростям. На основании теории вероятности Максвелл установил закономерность, по которой можно определить число молекул газа, скорости которых при данной температуре заключены в некотором интервале скоростей. Определяются функцией распределения Максвелла:
Распределение Максвелла достигает максимума при скорости
|
||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 561; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.203.143 (0.006 с.) |

 совокупность {\displaystyle 6N} 6N канонических переменных N {\displaystyle N} частиц ({\displaystyle 3N} 3N координат и 3N {\displaystyle 3N} импульсов), {\displaystyle a} a - совокупность внешних параметров, H(X,a) {\displaystyle H(X,a)} — гамильтониан системы,
совокупность {\displaystyle 6N} 6N канонических переменных N {\displaystyle N} частиц ({\displaystyle 3N} 3N координат и 3N {\displaystyle 3N} импульсов), {\displaystyle a} a - совокупность внешних параметров, H(X,a) {\displaystyle H(X,a)} — гамильтониан системы,  {\displaystyle \beta }- параметр распределения.
{\displaystyle \beta }- параметр распределения. , где обратная температура определена как
, где обратная температура определена как  , k — это постоянная Больцмана.
, k — это постоянная Больцмана.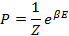

 будет обнаружено
будет обнаружено  частиц из
частиц из 
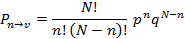
 .
. , то
, то 
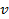 какого-либо числа частиц (от нуля до
какого-либо числа частиц (от нуля до  при фиксированных
при фиксированных  очень мала, т.к. при этом
очень мала, т.к. при этом  или
или 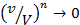 .
. . Если
. Если  , то бином Ньютона превращается в биноминальное распределение
, то бином Ньютона превращается в биноминальное распределение . Биноминальное распределение соответствует распределению вероятности того, что при
. Биноминальное распределение соответствует распределению вероятности того, что при  ) реализуется
) реализуется 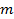 раз. В случае больших
раз. В случае больших  . Дифференцируя это выражение по
. Дифференцируя это выражение по  , где
, где  и
и  можно воспользоваться формулой Стирлинга
можно воспользоваться формулой Стирлинга
 - распределение Пуассона.
- распределение Пуассона. или пользуясь формулой Стирлинга
или пользуясь формулой Стирлинга 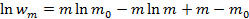 . Разложим последнее выражение в ряд Тейлора вблизи точки m=m0, ограничиваясь квадратичным членом, получим
. Разложим последнее выражение в ряд Тейлора вблизи точки m=m0, ограничиваясь квадратичным членом, получим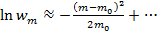 или
или  - называется распределением Гаусса
- называется распределением Гаусса

 {\displaystyle p\cdot V_{M}=R\cdot T}— закон Бойля — Мариотта.
{\displaystyle p\cdot V_{M}=R\cdot T}— закон Бойля — Мариотта. — Закон Гей-Люссака.
— Закон Гей-Люссака. — закон Шарля
— закон Шарля
 где
где  , имеет вид
, имеет вид
 , т.е. такой скорсти, к которой близки скорости большинства молекул.
, т.е. такой скорсти, к которой близки скорости большинства молекул.


