
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическое описание диамагнетизма.Содержание книги
Поиск на нашем сайте
Атомы и молекулы диамагнетиков в отсутствии магнитного поля не имеют магнитного момента, хотя, в рамках классической физики, в них вращаются по круговым орбитам электроны. Если диамагнетик находится во внешнем магнитном поле, то его магнитная проницаемость меньше единицы, т. е. магнитная индукция поля в диамагнетике меньше, чем магнитная индукция внешнего поля. Включим внешнее магнитное поле в пространстве, в котором расположен диамагнетик. Пусть линии индукции перпендикулярны плоскости орбиты какого - либо электрона (рис.178). Так как при этом:
Следовательно, возникает вихревое электрическое поле, вызывающее дополнительное вращение электрона – индукционный ток, который, в соответствии с правилом Ленца, имеет такое направление, чтобы индукционное магнитное поле противодействовало изменению внешнего поля. Что представляет собой это дополнительное вращение? Взаимодействие электрона с ядром значительно превышает воздействие внешнего поля и, поэтому радиус электронной орбиты в магнитном поле измениться не может. Движение электрона в атоме можно характеризовать моментом импульса и магнитным моментом. Дополнительное вращение характеризуется скоростью изменения момента импульса, которая, как известно, определяется моментом действующих сил: Следовательно:. Из этого выражения следует, что за малый единичный промежуток времени приращение момента импульса перпендикулярно плоскости проходящей через Из рисунка видно, что вектор момента импульса, а вместе с ним и ось орбиты описывают конус, ось которого направлена вдоль вектора магнитной индукции. Такое движение называется прецессией. Следовательно, под воздействием магнитного поля происходит прецессия электронной орбиты – прецессия Лармора (рис.180). Сравним полученное выражение с уравнением движения точки тела, вращающегося с угловой скоростью
РИС.178 РИС.179 РИС.180 РИС.181 изменения момента импульса, можно интерпретировать как вращение вектора момента импульса с угловой скоростью: Отсюда следует, что кинетическая энергия электрона изменяется, но ранее обсуждалось, что силы магнитного поля перпендикулярны скорости электрона и поэтому работы не совершают. Объяснить изменение кинетической энергии электрона можно работой вихревого электрического поля, которое возникает при всяком изменении магнитного. Если вектор магнитной индукции внешнего поля коллинеарен угловой скорости вращения электрона в атоме, то полная частота вращения электрона равна сумме его угловой скорости вращения в атоме и ларморовой частоты. Более вероятен вариант, когда линии индукции магнитного поля не перпендикулярны плоскости орбиты электрона, а значит орбитальный магнитный момент и, соответственно, момент импульса, составляет с вектором индукции некоторый угол (рис.179). Ларморова частота одинакова для всех электронов атома, т. е. возникает дополнительное вращение всей электронной оболочки атома. Поэтому говорят, что атом магнетика совершает, подобно гироскопу, прецессионное движение. Прецессионное движение электронных орбит эквивалентно, как уже обсуждалось, индукционному току, который создает индукционное магнитное поле, противоположное внешнему. Таким образом, явление диамагнетизма обусловлено ларморовой прецессией электронных орбит, которая должна наблюдаться для атомов любых веществ, но зарегистрировать это явление возможно только для атомов, не обладающих магнитным моментом. Следовательно, явление диамагнетизма универсально и обусловлено электромагнитной индукцией. Гиромагнитное отношение. Механический момент электрона тесно связан с его магнитным моментом. В теории магнетизма широко используют так называемые гиромагнитные отношения ¡=m/L. Для орбитального момента электрона Опыты Эйнштейна-де-Гааза. В 1915. Сущность опыта: если намагнитить железный стержень, то орбитальные магнитные моменты электронов установятся вдоль поля Н (а механические моменты против поля). В итоге суммарный механический момент электронов åLi уже будет отличаться о нуля (в отличии от первоначального состояния хаотических ориентаций механических моментов). С другой стороны, по закону сохранения момента импульса, полный момент импульса системы (стержень + электроны) должен остаться неизменным. Значит, стержень приобретает момент импульса, равный -åLi, т.е. придет во вращение. Если изменить направление намагниченности стержня на противоположное, то стержень будет вращаться в обратную сторону. Опыт позволил определить гиромагнитное соотношение ¡, которое вопреки ожиданиям, оказалось равным не ¡ =1, а ¡ =2. Опыт Барнетта. Еще одним доказательством связи ферромагнетизма со спиновым магнитным моментом электронов служит механомагнитный опыт Барнетта (1909 г.). Небольшой железный стержень приводился в быстрое (более 100 об/с) вращение вокруг своей оси. При этом наблюдалось слабое намагничивание стержня, и на том его конце, где вращение происходило по часовой стрелке, возникал северный полюс, а на противоположном − южный. Причиной эффекта Барнетта является тот факт, что электроны в атомах, обладая магнитным моментом, обладают и определенным моментом количества движения. Как было показано ранее, оба этих момента связаны друг с другом гиромагнитным соотношением, поэтому при вращении цилиндра «электронные волчки» будут стремиться, подобно гироскопам, ориентироваться так, чтобы их моменты количества движения были параллельны оси вращения цилиндра. Такая упорядоченная ориентация моментов количества движения неизбежно приводит к упорядочению магнитных моментов, а значит, к намагничиванию железного стержня. Ферромагнетики. Ферромагнетиками называются вещества, в которых собственное (внутреннее) магнитное поле может в сотни и тысячи раз превосходить вызвавшее его внешнее магнитное поле. Их основные свойства: 1) в отличии от слабо магнитных веществ у ферромагнетиков магнитная восприимчивость c в сотни раз больше единицы (c>>1); 2) они обладают самопроизвольной (спонтанной) намагниченностью в отсутствие внешнего поля Н (постоянные магниты).; 3) у каждого ферромагнитного вещества существует определённая температура Тс (точка Кюри), выше которых спонтанная намагниченность исчезает. Выше точки Кюри все ферромагнетики превращаются в парамагнетики. Доменная структура. Каждый реальный магнитный материал разделен по всему объему на множество замкнутых областей — доменов, в каждом из которых самопроизвольная намагниченность однородна и направлена по одной из осей легкой намагниченности. Такое состояние энергетически выгодно и кристалл в целом немагнитен, так как магнитные моменты доменов ориентированы в пространстве равновероятно. Между соседними доменами возникают граничные слои (стенки Блоха). Внутри доменных стенок векторы намагниченности плавно поворачиваются (рисунок 8.4). Объем доменов может колебаться в широких пределах (10-1¸10-6 см3).
Гистерезис намагничивания.
определяется внешними условиями не только в тот же, но и в предшествующие моменты времени. Неоднозначная зависимость величин наблюдается в любых процессах, т. к. для изменения состояния тела всегда требуется определённое время (время релаксации) и реакция тела отстаёт от вызывающих её причин. Такое отставание тем меньше, чем медленнее изменяются внешние условия, однако для некоторых процессов отставание при замедлении изменения внешних условий не уменьшается. В этих случаях неоднозначную зависимость величин называется гистерезисной, а само явление - Гистерезис
|
||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 392; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.192.109 (0.01 с.) |

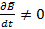 , то
, то  .
.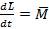 . Рассматривая движение электрона, как виток с током, находящийся в магнитном поле, можно записать, что:
. Рассматривая движение электрона, как виток с током, находящийся в магнитном поле, можно записать, что:  . Как уже обсуждалось, в рамках этих моделей:
. Как уже обсуждалось, в рамках этих моделей: 

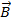 и
и 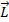 (рис.179).
(рис.179). :
:  (рис.181). Это сравнение показывает, что выражение для скорости
(рис.181). Это сравнение показывает, что выражение для скорости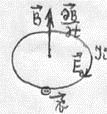



 , которая называется ларморовой частотой и характеризует дополнительную угловую скорость электрона.
, которая называется ларморовой частотой и характеризует дополнительную угловую скорость электрона. . m- орбитальный магнитный момент, L- механический магнитный момент. В других случаях гиромагнитное отношение записывают в виде
. m- орбитальный магнитный момент, L- механический магнитный момент. В других случаях гиромагнитное отношение записывают в виде  , где g- фактор Лонде.
, где g- фактор Лонде.  Ширина границы между антипараллельными доменами для железа 13.10-8 м, то есть около 500 элементарных ячеек. Толщина границы зависит главным образом от соотношения энергий: обменной, магнитной анизотропии и магнитоупругой. Размеры самих доменов зависят от неметаллических включений, границ зерен, скоплений дислокаций и других неоднородностей. Обычно домены имеют правильную форму.
Ширина границы между антипараллельными доменами для железа 13.10-8 м, то есть около 500 элементарных ячеек. Толщина границы зависит главным образом от соотношения энергий: обменной, магнитной анизотропии и магнитоупругой. Размеры самих доменов зависят от неметаллических включений, границ зерен, скоплений дислокаций и других неоднородностей. Обычно домены имеют правильную форму. На рисунке 8.5 показана: идеализированная доменная структура кристаллического ферромагнетика
На рисунке 8.5 показана: идеализированная доменная структура кристаллического ферромагнетика Гистерезис, явление, которое состоит в том, что физическая величина, характеризующая состояние тела (например, намагниченность), неоднозначно зависит от физические величины, характеризующей внешние условия (например, магнитного поля). Гистерезис наблюдается в тех случаях, когда состояние тела в данный момент времени
Гистерезис, явление, которое состоит в том, что физическая величина, характеризующая состояние тела (например, намагниченность), неоднозначно зависит от физические величины, характеризующей внешние условия (например, магнитного поля). Гистерезис наблюдается в тех случаях, когда состояние тела в данный момент времени


