

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Основы квантовой теории твердого тела.
Под твердыми телами понимают вещества, которые обладают некоторой жесткостью по отношию к сдвигу. Структура таких веществ обычно является кристаллической. С учетом дискретного атомного строения кристаллы – это вещества, в которых составляющие их частицы (атомы, молекулы) расположены строго периодически, образуя геометрическую закономерную кристаллическую структуру. Структура кристалла – это физ. реальность. Когда говгорят о структуре кристалла, то имеют ввиду конкретное расположение частиц (например, центров масс атомов) в кристаллич. пр-ве Пр-венная же решетка, основная роль к-рой свод-ся к размножению идентичных точек, не обязательно материальных, явл-ся лишь геометрич. постоением, помогающим выявить з-ны симметрии стр-ры кристалла. Решетку м\о описать с помощью периодически повторяющегося в пр-ве элементарного параллелепипеда – элементарной ячейки. Элементарная ячейка в общем случае предст. собой косоугольный параллелепипед. Схема уровней кристалла д\а вытекать из схемы уровней частиц, образующих кристалл и нах-ся под воздействием сил связи в решетке. Нижним энергетическим уровням, не возмущенным силами связи в решетке, м\о сопоставлять по желанию состояния электронов, принадлежащих одному единственному атому, или же состояния электронов всех атомов, образующих решетку. В обл-ти более высоких уровней (после М оболочки), возмущения, вызванные силами связи в решетке, становятся при возрастании энергии уровнней все более заметными. Уровни испытывают возмущение под влиянием все более и более обширных участков кристаллич. решетки. Эти возмущенные, близко примыкающие к друг другу уровни образ-ют в своей сов-ти широкие полосы.Разности энергий 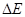 м\у соседними полосами уровней имеют порядок величины в неск-ко эВ. В рамках представления о боровских орбитах растущее влияние все более обширных участков кристаллич. решетки легко объяснить. Протяженные орбиты электрона, первоначально связанного с каким-то одним ядром, во все возрастающей степени вторгаются в обл-ти, занятые соседними ядрами. При этом все больше утрачивается возможность приписывать данный электрон определенному ядру. По отнош-ю к наиб. высоким уровням любая попытка говорить от такой принадлежности становится бессмысленной. Электроны нах-ся под совокупным влиянием всех частиц, образующих решетку. Наивысшие уровни принадлежат решетке как целому, они уже не имеют никакого отнош-я к уровням отдельных частиц, образующих решетку. Над зачерненными полосами располагаются заштрихованные полосы, образованные незаполненными уровнями. Состояния, соответствующие этим уровням, м\б достигнуты при оптичесчком или термическом возбуждении кристалла, они также принадлежат кристаллу как целому. Электрон, попавший в незанятую полосу, не имеет определенного положения в кристалле, он обладает свободной подвижностью. Незанятая или не полностью занятая полоса явл-ся «полосой проводимости». Электроны твердого тела движ-ся в электрическом поле атомных ядер, а также взаимод-ют м\у собой. Среди различных методов приближенного рассмотрения общей сложной задачи движ-я таких электронов оказался весьма плодотворным метод одноэлектронного приближения. Согласно этому методу движ-е многих электронов заменяется движ-ем одного электрона в поле заданного эффективного потенциала, учитывающего наряду с полем ядер частично и взаимод-е с остальными электронами. Волн. ф-ция одноэлектронной задачи д\а, т.о. удовлетворять стационарному ур-ю Шредингера м\у соседними полосами уровней имеют порядок величины в неск-ко эВ. В рамках представления о боровских орбитах растущее влияние все более обширных участков кристаллич. решетки легко объяснить. Протяженные орбиты электрона, первоначально связанного с каким-то одним ядром, во все возрастающей степени вторгаются в обл-ти, занятые соседними ядрами. При этом все больше утрачивается возможность приписывать данный электрон определенному ядру. По отнош-ю к наиб. высоким уровням любая попытка говорить от такой принадлежности становится бессмысленной. Электроны нах-ся под совокупным влиянием всех частиц, образующих решетку. Наивысшие уровни принадлежат решетке как целому, они уже не имеют никакого отнош-я к уровням отдельных частиц, образующих решетку. Над зачерненными полосами располагаются заштрихованные полосы, образованные незаполненными уровнями. Состояния, соответствующие этим уровням, м\б достигнуты при оптичесчком или термическом возбуждении кристалла, они также принадлежат кристаллу как целому. Электрон, попавший в незанятую полосу, не имеет определенного положения в кристалле, он обладает свободной подвижностью. Незанятая или не полностью занятая полоса явл-ся «полосой проводимости». Электроны твердого тела движ-ся в электрическом поле атомных ядер, а также взаимод-ют м\у собой. Среди различных методов приближенного рассмотрения общей сложной задачи движ-я таких электронов оказался весьма плодотворным метод одноэлектронного приближения. Согласно этому методу движ-е многих электронов заменяется движ-ем одного электрона в поле заданного эффективного потенциала, учитывающего наряду с полем ядер частично и взаимод-е с остальными электронами. Волн. ф-ция одноэлектронной задачи д\а, т.о. удовлетворять стационарному ур-ю Шредингера  где оператор Гамильтона где оператор Гамильтона  включает в себя эффективную потенциальную энергию V(r). Ф-ция V(r) д\а обладать трансляционной симметрией, т.е. явл-ся периодической ф-цией с периодом решетки V(r+n)=V(r). В действит-ти валентные электроны в кристалле движ-ся не вполне свободно – на них действует периодическое поле решетки. Это обстоят-во приводит к тому, что спектр возможных знач-й энергии валентных электронов распадается на ряд чередующихся разрешенных и запрещенных зон. В пределах разрешенных зон энергия изменяется квазинепрерывно. Знач-я энергии, принадлежащие запрещенным зонам, не м\т реализоваться. Зоны квазинепрерывно изменяющейся энергии чередуются с запрещенными зонами. Каждая разрешенная зона состоит из близко расположенных дискретных уровней, число к-рых = кол-ву атомов в образце кристалла. Обл-ть k-пр-ва (k-волн. вектор), внутри к-рой энергия электрона в кристалле изменяется квазинепрерывно, наз-ся зоной Бриллюэна. На границах зон энергия терпит разрыв. Основываясь на зонной стр-ре энергетич. спектра тв. тел, классифицируем их электропроводящие св-ва в зав-ти от хар-ра заполнения этих зон электронами. Будем предпол., что в нормальном состоянии тв. тела электроны стремятся занять наинизшее энергетич. состояние (при темп-ре абсолютного нуля электроны заполняют все энергетич. уровни вплоть до граничного верхнего уровня Ферми). Т.о., в основном состоянии кристалла будут заняты все состояния внутри некоторой пов-ти в пр-ве волновых векторов (импульсов) все же состояния вне этой пов-ти оказся свободными. Такая пов-ть наз-ся пов-тью Ферми. Соотв-щая энергия включает в себя эффективную потенциальную энергию V(r). Ф-ция V(r) д\а обладать трансляционной симметрией, т.е. явл-ся периодической ф-цией с периодом решетки V(r+n)=V(r). В действит-ти валентные электроны в кристалле движ-ся не вполне свободно – на них действует периодическое поле решетки. Это обстоят-во приводит к тому, что спектр возможных знач-й энергии валентных электронов распадается на ряд чередующихся разрешенных и запрещенных зон. В пределах разрешенных зон энергия изменяется квазинепрерывно. Знач-я энергии, принадлежащие запрещенным зонам, не м\т реализоваться. Зоны квазинепрерывно изменяющейся энергии чередуются с запрещенными зонами. Каждая разрешенная зона состоит из близко расположенных дискретных уровней, число к-рых = кол-ву атомов в образце кристалла. Обл-ть k-пр-ва (k-волн. вектор), внутри к-рой энергия электрона в кристалле изменяется квазинепрерывно, наз-ся зоной Бриллюэна. На границах зон энергия терпит разрыв. Основываясь на зонной стр-ре энергетич. спектра тв. тел, классифицируем их электропроводящие св-ва в зав-ти от хар-ра заполнения этих зон электронами. Будем предпол., что в нормальном состоянии тв. тела электроны стремятся занять наинизшее энергетич. состояние (при темп-ре абсолютного нуля электроны заполняют все энергетич. уровни вплоть до граничного верхнего уровня Ферми). Т.о., в основном состоянии кристалла будут заняты все состояния внутри некоторой пов-ти в пр-ве волновых векторов (импульсов) все же состояния вне этой пов-ти оказся свободными. Такая пов-ть наз-ся пов-тью Ферми. Соотв-щая энергия  отсчитанная от дна зоны наз-ся энергией Ферми. В случае почти свободных электронов, энергия к-рых квадратично зависит от импульса, пов-ть ферми предст. собой сферу отсчитанная от дна зоны наз-ся энергией Ферми. В случае почти свободных электронов, энергия к-рых квадратично зависит от импульса, пов-ть ферми предст. собой сферу 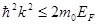 (сфера Ферми). Стр-ра зон энергии твердого тела и хар-р их заполнения (положение уровня Ферми) позволяют разделить твердые тела по хар-ру их проводимости. 1. Проводники. Хар-ной чертой проводников (металлов) явл-ся сущ-ние в основном сосотоянии частично заполненных зон разрешенных знач-й энергии (см.рис.) (сфера Ферми). Стр-ра зон энергии твердого тела и хар-р их заполнения (положение уровня Ферми) позволяют разделить твердые тела по хар-ру их проводимости. 1. Проводники. Хар-ной чертой проводников (металлов) явл-ся сущ-ние в основном сосотоянии частично заполненных зон разрешенных знач-й энергии (см.рис.)
Действ-но, электроны в тв. теле м\о себе представить разбитыми на пары, в каждой из к-рых электроны движ-ся в противоположных направлениях с одинаковой скоростью. Тогда средний ток оказ-ся =0, поск-ку токи, текущие в различных направлениях, взаимно компенсируются. В случае не полностью заполненной зоны такое статистич. равновесие м\б легко нарушено, например, наложением слабого электростатич. поля. Тогда электрон переходит на близлежащий свободный уровень, и средняя скорость электронов станов-ся  – появл-ся ток. Поск-ку уровни энергии вблизи границы Ферми распол-ся близко друг к другу, возникновение тока м\т произойти при наложении весьма слабого поля. Такая картина заполнения энергетич. уровней свойственны металлам. Собственная проводимость.При возбуждении электрона он перебрасывается из нижней зоны ч\з энергетическую щель в более высокорасположенную зону (см.рис). Одновременно в заполненной зоне образ-ся пустое место – «дырка». Движ-е дырки оказ-ся возможным интерпретировать как движ-е положительно заряженной частицы. Т.о., проводимость чистого полупроводника (собственная проводимость) м\т рассматриваться ка движ-е электронов в верхней зоне (электронная проводимость) и движ-е дырок в нижней почти заполненной зоне (дырочная проводимость). 2. Примесная проводимость. Включение примесей в кристалл полупроводника м\т оказ-ть сущ-венное влияние на его проводимость. Атомы примеси м\т отдавать свои электроны в свободную зону проводимости кристалла – так наз. донорные примеси, тогда в процессе проводимости участвуют электроны, к-рые движ-ся в незаполненной зоне проводимости. Такие электроны наз-ся электронами проводимости, а полупроводники, легированные донорами, наз-ся полупроводниками n-типа. Атомы примеси м\т захватывать электроны из нижней заполненной зоны кристалла – так наз. акцепторные примеси. Тогда в почти заполненной нижней зоне образ-ся дырка, движ-е к-рой м\о рассм-ть как движ-е положительно заряженной частицы. Полупроводники, легированные акцепторами, обладают дырочной проводимостью, и наз-ся полупроводниками р-типа. (см.рис.) Таковы основные следствия зонной теории энергетич. спектра, к-рые объясняют проводимость тв. тел. На электропроводность сущ-венное влияние м\т оказ-ть дефекты решетки. Выделяют 4 класса дефектов. Точечные (нульмерные) дефекты. Нарушения стр-ры локализованы в отдельных точках кристалла. Размеры указанных дефектов во всех трех измерениях не превышают одного или неск-ких межатомных расстояний. К точечным дефектам относят вакансии (вакантные узлы кристаллич. решетки), атомы в междоузлиях, атомы примесей в узлах или междоузлиях, сочетания примесь-вакансия, примесь-примесь, двойные и тройные вакансии и др. Линейные (одномерные) дефекты хар-ся тем, чтио нарушения периодичности простираются в одном измерении на расстояния, много большие параметра решетки, тогда как в двух других измерениях они не превышают неск-ких параметров. Линейными дефектами явл-ся дислокации, микротрещины. Поверхностные (двухмерные) дефекты в двух измерениях имеют размеры, во много раз превышающие параметр решетки, а в третьем – неск-ко параметров. Границы зерен и двойников, дефекты упаковки, межфазные границы, стенки доменов, а также пов-ть кристалла предст. собой двухмерные дефекты. Объемные дефекты этот микропустоты и включения другой фазы. Они возниккают обычно при выращивании кристаллов или в рез-те некоторых воздействий на кристалл. Двухмерные дефекты м\б следствием наличия примесей в расплаве. Дислокации возникают в рез-те пластической деформации кристалла в процессе роста или при последующих обработках. Точечные дефекты м\т появиться в твердых телах вследствие нагревания (тепловые дефекты), облучения быстрыми частицами (радиационные дефекты), пластической деформации. Рассм. движ-е электронов в зоне проводимости и введем понятие эффективной массы. В общем случае движ-я электронов в кристалле, кинетич. и потенциальная энергии ведут себя довольно сложным образом. Полная энергия частицы поэтому не м\б выражена элементарно так, как это было в случае свободного движ-я. Рассм. для простоты одномерный кристалл и разложим энергию E(k) в ряд Тейлора в окрестности точки – появл-ся ток. Поск-ку уровни энергии вблизи границы Ферми распол-ся близко друг к другу, возникновение тока м\т произойти при наложении весьма слабого поля. Такая картина заполнения энергетич. уровней свойственны металлам. Собственная проводимость.При возбуждении электрона он перебрасывается из нижней зоны ч\з энергетическую щель в более высокорасположенную зону (см.рис). Одновременно в заполненной зоне образ-ся пустое место – «дырка». Движ-е дырки оказ-ся возможным интерпретировать как движ-е положительно заряженной частицы. Т.о., проводимость чистого полупроводника (собственная проводимость) м\т рассматриваться ка движ-е электронов в верхней зоне (электронная проводимость) и движ-е дырок в нижней почти заполненной зоне (дырочная проводимость). 2. Примесная проводимость. Включение примесей в кристалл полупроводника м\т оказ-ть сущ-венное влияние на его проводимость. Атомы примеси м\т отдавать свои электроны в свободную зону проводимости кристалла – так наз. донорные примеси, тогда в процессе проводимости участвуют электроны, к-рые движ-ся в незаполненной зоне проводимости. Такие электроны наз-ся электронами проводимости, а полупроводники, легированные донорами, наз-ся полупроводниками n-типа. Атомы примеси м\т захватывать электроны из нижней заполненной зоны кристалла – так наз. акцепторные примеси. Тогда в почти заполненной нижней зоне образ-ся дырка, движ-е к-рой м\о рассм-ть как движ-е положительно заряженной частицы. Полупроводники, легированные акцепторами, обладают дырочной проводимостью, и наз-ся полупроводниками р-типа. (см.рис.) Таковы основные следствия зонной теории энергетич. спектра, к-рые объясняют проводимость тв. тел. На электропроводность сущ-венное влияние м\т оказ-ть дефекты решетки. Выделяют 4 класса дефектов. Точечные (нульмерные) дефекты. Нарушения стр-ры локализованы в отдельных точках кристалла. Размеры указанных дефектов во всех трех измерениях не превышают одного или неск-ких межатомных расстояний. К точечным дефектам относят вакансии (вакантные узлы кристаллич. решетки), атомы в междоузлиях, атомы примесей в узлах или междоузлиях, сочетания примесь-вакансия, примесь-примесь, двойные и тройные вакансии и др. Линейные (одномерные) дефекты хар-ся тем, чтио нарушения периодичности простираются в одном измерении на расстояния, много большие параметра решетки, тогда как в двух других измерениях они не превышают неск-ких параметров. Линейными дефектами явл-ся дислокации, микротрещины. Поверхностные (двухмерные) дефекты в двух измерениях имеют размеры, во много раз превышающие параметр решетки, а в третьем – неск-ко параметров. Границы зерен и двойников, дефекты упаковки, межфазные границы, стенки доменов, а также пов-ть кристалла предст. собой двухмерные дефекты. Объемные дефекты этот микропустоты и включения другой фазы. Они возниккают обычно при выращивании кристаллов или в рез-те некоторых воздействий на кристалл. Двухмерные дефекты м\б следствием наличия примесей в расплаве. Дислокации возникают в рез-те пластической деформации кристалла в процессе роста или при последующих обработках. Точечные дефекты м\т появиться в твердых телах вследствие нагревания (тепловые дефекты), облучения быстрыми частицами (радиационные дефекты), пластической деформации. Рассм. движ-е электронов в зоне проводимости и введем понятие эффективной массы. В общем случае движ-я электронов в кристалле, кинетич. и потенциальная энергии ведут себя довольно сложным образом. Полная энергия частицы поэтому не м\б выражена элементарно так, как это было в случае свободного движ-я. Рассм. для простоты одномерный кристалл и разложим энергию E(k) в ряд Тейлора в окрестности точки  выберем далее точку выберем далее точку  так, чтобы она соответствовала экстремуму ф-ции E(k), и положим так, чтобы она соответствовала экстремуму ф-ции E(k), и положим  где эффективная масса m* равна где эффективная масса m* равна 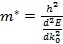 Т.о. в указанном приближении (приближение Блоха) электрон в полосе разрешенных знач-й энергии движ-ся как частица с эффективной массой m*. Легко заметить что эффективная масса электрона отлич-ся от истинной – это отличие кас-ся и абсолютной величины и знака. Действит-но, пусть электрон движ-ся в зоне проводимости, содержащей небольшое число частиц. Тогда электрон нах-ся в состояниях, близких к дну зоны (т.е. к минимуму энергии), и поэтому Т.о. в указанном приближении (приближение Блоха) электрон в полосе разрешенных знач-й энергии движ-ся как частица с эффективной массой m*. Легко заметить что эффективная масса электрона отлич-ся от истинной – это отличие кас-ся и абсолютной величины и знака. Действит-но, пусть электрон движ-ся в зоне проводимости, содержащей небольшое число частиц. Тогда электрон нах-ся в состояниях, близких к дну зоны (т.е. к минимуму энергии), и поэтому  - точка минимума E(k), а - точка минимума E(k), а  Сл-но, электронная проводимость хар-ся положительной эффективной массой. Напротив, если в энергетич. зоне много электронов (почти заполненная зона), то Сл-но, электронная проводимость хар-ся положительной эффективной массой. Напротив, если в энергетич. зоне много электронов (почти заполненная зона), то  будет соответствовать максимуму энергии, при этом, очевидно, будет соответствовать максимуму энергии, при этом, очевидно, 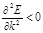 и эффективная масса отрицательна. и эффективная масса отрицательна.
Уравнения Максвелла
Электромагнитное поле - это область пространства, в которой наблюдаются электромагнитные взаимодействия (например пробного заряда в конкретной точке пространства с этим полем).
Уравнения Максвелла представляют собой наиболее общее выражение законов электромагнетизма, охватывающее известные экспериментальные и теоретические данные, поэтому используются как инструмент для решения задач теории поля.
Максвелл ввел понятия тока смещения как некоторого электрического процесса в диэлектрической среде под действием ЭМП. Он противопоставил этот ток току проводимости по физической сущности и отождествлял их в части созданном магнитном поле.
В проводах протекает ток проводимости, а в пространстве между обкладками тока проводимости нет, но имеется электрическое поле, образованное зарядами, сосредоточенными на обкладках и изменяющими во времени свою величину и знак. Электрическая цепь замкнута, то есть ток проводимости замыкается током, названным током смещения.
Ток смещения по Максвеллу определяется уравнением
 (1.5) (1.5)
где 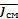 – вектор плотности тока смещения. – вектор плотности тока смещения.
Ток проводимости по Максвеллу
 (1.6) (1.6)
где  - плотность тока проводимости. - плотность тока проводимости.
Максвелл установил связь между векторами  в форме уравнений, вытекающих из физической трактовки электромагнитных процессов, изученных Фарадеем, Ампером и др. учеными. в форме уравнений, вытекающих из физической трактовки электромагнитных процессов, изученных Фарадеем, Ампером и др. учеными.


С помощью этих уравнений можно создать модель распространения электромагнитного поля
Поляризация электромагнитных волн определяется тем, как ведет себя вектор напряжянности электрического поля по мере его распространения. Волна называется линейно поляризованной, если вектор Е, изменяясь во времени, остается параллельным некоторому направлению, которое и является направлением поляризации волны.
Уравнения Максвелла.
В интегральной форме:

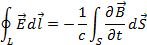
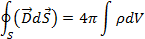

| В дифференциальной форме:


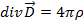

| В вакууме скорость распространения электромагнитной волны с ≈300 000 км/с (см. Скорость света). В однородных изотропных средах направления напряжённостей электрического (Е) и магнитного (Н) полей электромагнитной волны перпендикулярны друг другу и направлению распространения волны, то есть электромагнитная волна является поперечной.
Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
 (в системе СГС), (в системе СГС),
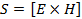 (в СИ), (в СИ),
где E и H — векторы напряжённости электрического и магнитного полей соответственно.
В электродинамике закон сохранения энергии исторически формулируется в виде теоремы Пойтинга.
Изменение электромагнитной энергии, заключенной в неком объеме, за некий интервал времени равно потоку электромагнитной энергии через поверхность, ограничивающую данный объем, и количеству тепловой энергии, выделившейся в данном объеме, взятой с обратным знаком.

ДИПОЛЬНОЕ ИЗЛУЧЕНИЕ излучение электромагнитных волн, обусловл. изменением во времени электрич. дипольного момента излучающей системы (электрическое Д. и.) или её магнитного момента (магнитное Д. и.).
|



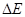 м\у соседними полосами уровней имеют порядок величины в неск-ко эВ. В рамках представления о боровских орбитах растущее влияние все более обширных участков кристаллич. решетки легко объяснить. Протяженные орбиты электрона, первоначально связанного с каким-то одним ядром, во все возрастающей степени вторгаются в обл-ти, занятые соседними ядрами. При этом все больше утрачивается возможность приписывать данный электрон определенному ядру. По отнош-ю к наиб. высоким уровням любая попытка говорить от такой принадлежности становится бессмысленной. Электроны нах-ся под совокупным влиянием всех частиц, образующих решетку. Наивысшие уровни принадлежат решетке как целому, они уже не имеют никакого отнош-я к уровням отдельных частиц, образующих решетку. Над зачерненными полосами располагаются заштрихованные полосы, образованные незаполненными уровнями. Состояния, соответствующие этим уровням, м\б достигнуты при оптичесчком или термическом возбуждении кристалла, они также принадлежат кристаллу как целому. Электрон, попавший в незанятую полосу, не имеет определенного положения в кристалле, он обладает свободной подвижностью. Незанятая или не полностью занятая полоса явл-ся «полосой проводимости». Электроны твердого тела движ-ся в электрическом поле атомных ядер, а также взаимод-ют м\у собой. Среди различных методов приближенного рассмотрения общей сложной задачи движ-я таких электронов оказался весьма плодотворным метод одноэлектронного приближения. Согласно этому методу движ-е многих электронов заменяется движ-ем одного электрона в поле заданного эффективного потенциала, учитывающего наряду с полем ядер частично и взаимод-е с остальными электронами. Волн. ф-ция одноэлектронной задачи д\а, т.о. удовлетворять стационарному ур-ю Шредингера
м\у соседними полосами уровней имеют порядок величины в неск-ко эВ. В рамках представления о боровских орбитах растущее влияние все более обширных участков кристаллич. решетки легко объяснить. Протяженные орбиты электрона, первоначально связанного с каким-то одним ядром, во все возрастающей степени вторгаются в обл-ти, занятые соседними ядрами. При этом все больше утрачивается возможность приписывать данный электрон определенному ядру. По отнош-ю к наиб. высоким уровням любая попытка говорить от такой принадлежности становится бессмысленной. Электроны нах-ся под совокупным влиянием всех частиц, образующих решетку. Наивысшие уровни принадлежат решетке как целому, они уже не имеют никакого отнош-я к уровням отдельных частиц, образующих решетку. Над зачерненными полосами располагаются заштрихованные полосы, образованные незаполненными уровнями. Состояния, соответствующие этим уровням, м\б достигнуты при оптичесчком или термическом возбуждении кристалла, они также принадлежат кристаллу как целому. Электрон, попавший в незанятую полосу, не имеет определенного положения в кристалле, он обладает свободной подвижностью. Незанятая или не полностью занятая полоса явл-ся «полосой проводимости». Электроны твердого тела движ-ся в электрическом поле атомных ядер, а также взаимод-ют м\у собой. Среди различных методов приближенного рассмотрения общей сложной задачи движ-я таких электронов оказался весьма плодотворным метод одноэлектронного приближения. Согласно этому методу движ-е многих электронов заменяется движ-ем одного электрона в поле заданного эффективного потенциала, учитывающего наряду с полем ядер частично и взаимод-е с остальными электронами. Волн. ф-ция одноэлектронной задачи д\а, т.о. удовлетворять стационарному ур-ю Шредингера  где оператор Гамильтона
где оператор Гамильтона  включает в себя эффективную потенциальную энергию V(r). Ф-ция V(r) д\а обладать трансляционной симметрией, т.е. явл-ся периодической ф-цией с периодом решетки V(r+n)=V(r). В действит-ти валентные электроны в кристалле движ-ся не вполне свободно – на них действует периодическое поле решетки. Это обстоят-во приводит к тому, что спектр возможных знач-й энергии валентных электронов распадается на ряд чередующихся разрешенных и запрещенных зон. В пределах разрешенных зон энергия изменяется квазинепрерывно. Знач-я энергии, принадлежащие запрещенным зонам, не м\т реализоваться. Зоны квазинепрерывно изменяющейся энергии чередуются с запрещенными зонами. Каждая разрешенная зона состоит из близко расположенных дискретных уровней, число к-рых = кол-ву атомов в образце кристалла. Обл-ть k-пр-ва (k-волн. вектор), внутри к-рой энергия электрона в кристалле изменяется квазинепрерывно, наз-ся зоной Бриллюэна. На границах зон энергия терпит разрыв. Основываясь на зонной стр-ре энергетич. спектра тв. тел, классифицируем их электропроводящие св-ва в зав-ти от хар-ра заполнения этих зон электронами. Будем предпол., что в нормальном состоянии тв. тела электроны стремятся занять наинизшее энергетич. состояние (при темп-ре абсолютного нуля электроны заполняют все энергетич. уровни вплоть до граничного верхнего уровня Ферми). Т.о., в основном состоянии кристалла будут заняты все состояния внутри некоторой пов-ти в пр-ве волновых векторов (импульсов) все же состояния вне этой пов-ти оказся свободными. Такая пов-ть наз-ся пов-тью Ферми. Соотв-щая энергия
включает в себя эффективную потенциальную энергию V(r). Ф-ция V(r) д\а обладать трансляционной симметрией, т.е. явл-ся периодической ф-цией с периодом решетки V(r+n)=V(r). В действит-ти валентные электроны в кристалле движ-ся не вполне свободно – на них действует периодическое поле решетки. Это обстоят-во приводит к тому, что спектр возможных знач-й энергии валентных электронов распадается на ряд чередующихся разрешенных и запрещенных зон. В пределах разрешенных зон энергия изменяется квазинепрерывно. Знач-я энергии, принадлежащие запрещенным зонам, не м\т реализоваться. Зоны квазинепрерывно изменяющейся энергии чередуются с запрещенными зонами. Каждая разрешенная зона состоит из близко расположенных дискретных уровней, число к-рых = кол-ву атомов в образце кристалла. Обл-ть k-пр-ва (k-волн. вектор), внутри к-рой энергия электрона в кристалле изменяется квазинепрерывно, наз-ся зоной Бриллюэна. На границах зон энергия терпит разрыв. Основываясь на зонной стр-ре энергетич. спектра тв. тел, классифицируем их электропроводящие св-ва в зав-ти от хар-ра заполнения этих зон электронами. Будем предпол., что в нормальном состоянии тв. тела электроны стремятся занять наинизшее энергетич. состояние (при темп-ре абсолютного нуля электроны заполняют все энергетич. уровни вплоть до граничного верхнего уровня Ферми). Т.о., в основном состоянии кристалла будут заняты все состояния внутри некоторой пов-ти в пр-ве волновых векторов (импульсов) все же состояния вне этой пов-ти оказся свободными. Такая пов-ть наз-ся пов-тью Ферми. Соотв-щая энергия  отсчитанная от дна зоны наз-ся энергией Ферми. В случае почти свободных электронов, энергия к-рых квадратично зависит от импульса, пов-ть ферми предст. собой сферу
отсчитанная от дна зоны наз-ся энергией Ферми. В случае почти свободных электронов, энергия к-рых квадратично зависит от импульса, пов-ть ферми предст. собой сферу 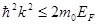 (сфера Ферми). Стр-ра зон энергии твердого тела и хар-р их заполнения (положение уровня Ферми) позволяют разделить твердые тела по хар-ру их проводимости. 1. Проводники. Хар-ной чертой проводников (металлов) явл-ся сущ-ние в основном сосотоянии частично заполненных зон разрешенных знач-й энергии (см.рис.)
(сфера Ферми). Стр-ра зон энергии твердого тела и хар-р их заполнения (положение уровня Ферми) позволяют разделить твердые тела по хар-ру их проводимости. 1. Проводники. Хар-ной чертой проводников (металлов) явл-ся сущ-ние в основном сосотоянии частично заполненных зон разрешенных знач-й энергии (см.рис.) – появл-ся ток. Поск-ку уровни энергии вблизи границы Ферми распол-ся близко друг к другу, возникновение тока м\т произойти при наложении весьма слабого поля. Такая картина заполнения энергетич. уровней свойственны металлам. Собственная проводимость.При возбуждении электрона он перебрасывается из нижней зоны ч\з энергетическую щель в более высокорасположенную зону (см.рис). Одновременно в заполненной зоне образ-ся пустое место – «дырка». Движ-е дырки оказ-ся возможным интерпретировать как движ-е положительно заряженной частицы. Т.о., проводимость чистого полупроводника (собственная проводимость) м\т рассматриваться ка движ-е электронов в верхней зоне (электронная проводимость) и движ-е дырок в нижней почти заполненной зоне (дырочная проводимость). 2. Примесная проводимость. Включение примесей в кристалл полупроводника м\т оказ-ть сущ-венное влияние на его проводимость. Атомы примеси м\т отдавать свои электроны в свободную зону проводимости кристалла – так наз. донорные примеси, тогда в процессе проводимости участвуют электроны, к-рые движ-ся в незаполненной зоне проводимости. Такие электроны наз-ся электронами проводимости, а полупроводники, легированные донорами, наз-ся полупроводниками n-типа. Атомы примеси м\т захватывать электроны из нижней заполненной зоны кристалла – так наз. акцепторные примеси. Тогда в почти заполненной нижней зоне образ-ся дырка, движ-е к-рой м\о рассм-ть как движ-е положительно заряженной частицы. Полупроводники, легированные акцепторами, обладают дырочной проводимостью, и наз-ся полупроводниками р-типа. (см.рис.) Таковы основные следствия зонной теории энергетич. спектра, к-рые объясняют проводимость тв. тел. На электропроводность сущ-венное влияние м\т оказ-ть дефекты решетки. Выделяют 4 класса дефектов. Точечные (нульмерные) дефекты. Нарушения стр-ры локализованы в отдельных точках кристалла. Размеры указанных дефектов во всех трех измерениях не превышают одного или неск-ких межатомных расстояний. К точечным дефектам относят вакансии (вакантные узлы кристаллич. решетки), атомы в междоузлиях, атомы примесей в узлах или междоузлиях, сочетания примесь-вакансия, примесь-примесь, двойные и тройные вакансии и др. Линейные (одномерные) дефекты хар-ся тем, чтио нарушения периодичности простираются в одном измерении на расстояния, много большие параметра решетки, тогда как в двух других измерениях они не превышают неск-ких параметров. Линейными дефектами явл-ся дислокации, микротрещины. Поверхностные (двухмерные) дефекты в двух измерениях имеют размеры, во много раз превышающие параметр решетки, а в третьем – неск-ко параметров. Границы зерен и двойников, дефекты упаковки, межфазные границы, стенки доменов, а также пов-ть кристалла предст. собой двухмерные дефекты. Объемные дефекты этот микропустоты и включения другой фазы. Они возниккают обычно при выращивании кристаллов или в рез-те некоторых воздействий на кристалл. Двухмерные дефекты м\б следствием наличия примесей в расплаве. Дислокации возникают в рез-те пластической деформации кристалла в процессе роста или при последующих обработках. Точечные дефекты м\т появиться в твердых телах вследствие нагревания (тепловые дефекты), облучения быстрыми частицами (радиационные дефекты), пластической деформации. Рассм. движ-е электронов в зоне проводимости и введем понятие эффективной массы. В общем случае движ-я электронов в кристалле, кинетич. и потенциальная энергии ведут себя довольно сложным образом. Полная энергия частицы поэтому не м\б выражена элементарно так, как это было в случае свободного движ-я. Рассм. для простоты одномерный кристалл и разложим энергию E(k) в ряд Тейлора в окрестности точки
– появл-ся ток. Поск-ку уровни энергии вблизи границы Ферми распол-ся близко друг к другу, возникновение тока м\т произойти при наложении весьма слабого поля. Такая картина заполнения энергетич. уровней свойственны металлам. Собственная проводимость.При возбуждении электрона он перебрасывается из нижней зоны ч\з энергетическую щель в более высокорасположенную зону (см.рис). Одновременно в заполненной зоне образ-ся пустое место – «дырка». Движ-е дырки оказ-ся возможным интерпретировать как движ-е положительно заряженной частицы. Т.о., проводимость чистого полупроводника (собственная проводимость) м\т рассматриваться ка движ-е электронов в верхней зоне (электронная проводимость) и движ-е дырок в нижней почти заполненной зоне (дырочная проводимость). 2. Примесная проводимость. Включение примесей в кристалл полупроводника м\т оказ-ть сущ-венное влияние на его проводимость. Атомы примеси м\т отдавать свои электроны в свободную зону проводимости кристалла – так наз. донорные примеси, тогда в процессе проводимости участвуют электроны, к-рые движ-ся в незаполненной зоне проводимости. Такие электроны наз-ся электронами проводимости, а полупроводники, легированные донорами, наз-ся полупроводниками n-типа. Атомы примеси м\т захватывать электроны из нижней заполненной зоны кристалла – так наз. акцепторные примеси. Тогда в почти заполненной нижней зоне образ-ся дырка, движ-е к-рой м\о рассм-ть как движ-е положительно заряженной частицы. Полупроводники, легированные акцепторами, обладают дырочной проводимостью, и наз-ся полупроводниками р-типа. (см.рис.) Таковы основные следствия зонной теории энергетич. спектра, к-рые объясняют проводимость тв. тел. На электропроводность сущ-венное влияние м\т оказ-ть дефекты решетки. Выделяют 4 класса дефектов. Точечные (нульмерные) дефекты. Нарушения стр-ры локализованы в отдельных точках кристалла. Размеры указанных дефектов во всех трех измерениях не превышают одного или неск-ких межатомных расстояний. К точечным дефектам относят вакансии (вакантные узлы кристаллич. решетки), атомы в междоузлиях, атомы примесей в узлах или междоузлиях, сочетания примесь-вакансия, примесь-примесь, двойные и тройные вакансии и др. Линейные (одномерные) дефекты хар-ся тем, чтио нарушения периодичности простираются в одном измерении на расстояния, много большие параметра решетки, тогда как в двух других измерениях они не превышают неск-ких параметров. Линейными дефектами явл-ся дислокации, микротрещины. Поверхностные (двухмерные) дефекты в двух измерениях имеют размеры, во много раз превышающие параметр решетки, а в третьем – неск-ко параметров. Границы зерен и двойников, дефекты упаковки, межфазные границы, стенки доменов, а также пов-ть кристалла предст. собой двухмерные дефекты. Объемные дефекты этот микропустоты и включения другой фазы. Они возниккают обычно при выращивании кристаллов или в рез-те некоторых воздействий на кристалл. Двухмерные дефекты м\б следствием наличия примесей в расплаве. Дислокации возникают в рез-те пластической деформации кристалла в процессе роста или при последующих обработках. Точечные дефекты м\т появиться в твердых телах вследствие нагревания (тепловые дефекты), облучения быстрыми частицами (радиационные дефекты), пластической деформации. Рассм. движ-е электронов в зоне проводимости и введем понятие эффективной массы. В общем случае движ-я электронов в кристалле, кинетич. и потенциальная энергии ведут себя довольно сложным образом. Полная энергия частицы поэтому не м\б выражена элементарно так, как это было в случае свободного движ-я. Рассм. для простоты одномерный кристалл и разложим энергию E(k) в ряд Тейлора в окрестности точки  выберем далее точку
выберем далее точку  так, чтобы она соответствовала экстремуму ф-ции E(k), и положим
так, чтобы она соответствовала экстремуму ф-ции E(k), и положим  где эффективная масса m* равна
где эффективная масса m* равна 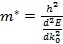 Т.о. в указанном приближении (приближение Блоха) электрон в полосе разрешенных знач-й энергии движ-ся как частица с эффективной массой m*. Легко заметить что эффективная масса электрона отлич-ся от истинной – это отличие кас-ся и абсолютной величины и знака. Действит-но, пусть электрон движ-ся в зоне проводимости, содержащей небольшое число частиц. Тогда электрон нах-ся в состояниях, близких к дну зоны (т.е. к минимуму энергии), и поэтому
Т.о. в указанном приближении (приближение Блоха) электрон в полосе разрешенных знач-й энергии движ-ся как частица с эффективной массой m*. Легко заметить что эффективная масса электрона отлич-ся от истинной – это отличие кас-ся и абсолютной величины и знака. Действит-но, пусть электрон движ-ся в зоне проводимости, содержащей небольшое число частиц. Тогда электрон нах-ся в состояниях, близких к дну зоны (т.е. к минимуму энергии), и поэтому  - точка минимума E(k), а
- точка минимума E(k), а  Сл-но, электронная проводимость хар-ся положительной эффективной массой. Напротив, если в энергетич. зоне много электронов (почти заполненная зона), то
Сл-но, электронная проводимость хар-ся положительной эффективной массой. Напротив, если в энергетич. зоне много электронов (почти заполненная зона), то 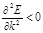 и эффективная масса отрицательна.
и эффективная масса отрицательна. (1.5)
(1.5)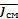 – вектор плотности тока смещения.
– вектор плотности тока смещения. (1.6)
(1.6) - плотность тока проводимости.
- плотность тока проводимости. в форме уравнений, вытекающих из физической трактовки электромагнитных процессов, изученных Фарадеем, Ампером и др. учеными.
в форме уравнений, вытекающих из физической трактовки электромагнитных процессов, изученных Фарадеем, Ампером и др. учеными.


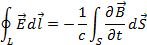
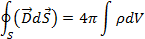



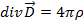

 (в системе СГС),
(в системе СГС),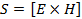 (в СИ),
(в СИ),



