Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Идеальные системы в статистической механикеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Идеальный газ из бозонов — бозе - газ — описывается квантовой статистикой Бозе — Эйнштейна (Шатьендранат Бозе – Индия). Распределение бозонов по энергиям вытекает из так называемого большого канонического распределения Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов в данном квантовом состоянии может быть любым:
Это распределение называется распределением Бозе — Эйнштейна. Здесь Идеальный газ из фермионов — ферми-газ — описывается квантовой статистикой Ферми — Дирака. Распред-ие фермионов по энергиям имеет вид
где
Если
Таким образом, при высоких температурах оба «квантовых» газа ведут себя подобно классическому газу. Система частиц называется вырожденной, если ее свойства существенным образом отличаются от свойств систем, подчиняющихся классической статистике. Поведение как бозе-газа, так и ферми-газа отличается от классического газа, они являются вырожденными газами. Вырождение газов становится существенным при весьма низких температурах и больших плотностях. Параметром вырождения называется величина А. При Температурой вырождения отчетливо проявляются квантовые свойства идеального газа, обусловленные тождественностью частиц, т. е. Т 0 — температура, при которой вырождение становится существенным. Если
Рассмотрим газ при температуре Функция распределения Ферми по квантовым состояниям (с опреде ленными значениями импульса р и проекции спина) нуль при ε > μ(на рис. 6 эта функция изображена сплошной линией). Химический потенциал газа при Т= 0 совпадает с граничной энергией электронов: ε = μ. Вырожденный электронный газ обладает своеобразной особенностью— он становится тем более идеальным, чем больше его плотность. По мере сжатия газа средняя энергия электронов увеличивается (растет εF); когда она становится сравнимой с mc2, делаются существенными релятивистские эффекты. С точки зрения фотонной теории, равновесное тепловое излучение можно представить в виде фотонного газа, заполняющего полость, частицы которого движутся хаотически, то есть равновероятно по всем направлениям. Числофотонов, падающих на единицу поверхности в единицу времени, запишется как Очевидно, что газ фотонов не может быть описан как классический идеальный газ. Частицы фотонного газа не имеют распределения по скоростям, а их распределение по энергиям не описывается классическим распределением Максвелла-Больцмана. Прежде всего, выведем уравнение состояния фотонного газа, связывающего для такого газа термодинамические параметры - давление, объем и температуру. Для этого, как и в молекулярно-кинетической теории газов, формулу для давления фотонного газа получим, рассмотрев процесс передачи импульса стенке сосуда падающими на нее фотонами. Для давления фотонного газа получаем формулу Здесь Итак, давление, которое оказывает фотонный газ, пропорционально четвертой степени его абсолютной температуры и не зависит от объема полости, в которой заключен фотонный газ, моделирующий в корпускулярной теории тепловое излучение, заполняющее полость. Замедление атомов с использованием охлаждающей аппаратуры позволяет получить сингулярное квантовое состояние, известное как конденсат Бозе, или Бозе — Эйнштейна. Статистика Бозе — Эйнштейна, которая описывает статистическое распределение тождественных частиц с целым спином, называемых бозонами. Бозоны, которыми являются, например, и отдельные элементарные частицы — фотоны, и целые атомы, могут находиться друг с другом в одинаковых квантовых состояниях. Эйнштейн предположил, что охлаждение атомов — бозонов до очень низких температур заставит их перейти (или, по-другому, сконденсироваться) в наинизшее возможное квантовое состояние. Результатом такой конденсации станет возникновение новой формы вещества. Этот переход возникает ниже критической температуры.
Физическая кинетика. Микроскопическое состояние системы многих частиц. А)Микроскопическое состояние можно представить как чистое механическое состояние: использ теорию квантов.мех:микроскопич состояние системы к-частиц заданно как чистое квантомеханическое состояние, если заданна волновая функция: А1, А2,... Будем теперь следить за дальнейшим передвижением фазовых точек.Передвижение фазовых точек будет происходить тогда согласно уравнениям механики, содержащим координаты и импульсы только частиц подсистемы. Ясно, что в каждый момент времени t с тем же правом, что к в момент t = 0, все эти точки будут распределены в фазовом простраистве согласно той же функции распределения. Другими словами, передвигаясь с течением времени, фазовые точки остаются распределенными с неизменной в каждом данном месте плотностью, пропорциональной соответствующему значению ρ. Чисто формальным образом это передвижение фазовых течек можно рассматривать как стационарное течение «газа» в 2s-Mepнoм фазовом пространстве и применить к нему известное уравнение непрерывности, выражающее собой неизменность общего числа «частиц» (в данном случае — фазовых точек) газа. Обычное уравнение непрерывности имеет вид dρ/dt+ div(ρv) = 0 (ρ — плотность, v—скорость газа), а для стационарного течения div(pv) = 0. Обобщение последнего соотношения на случай 2s-Mepнoro пространства
Поэтому второй член в (3,1) тождественно обращается в нуль. Первый же член есть не что иное, как полная производная от функции распределения по времени. Таким образом, имеем:
не продолжая процедуры построения следующих уравнений видим что уравнения для корреляционных функций образуют цепочку. Эти ур. не замкнутые.так что каждое следующее включает в себя предыдущее,так что решению этих уравнений должна предшествовать процедура расцепления цепочки, так что бы оставшееся группа уравнений оказалась замкнутой. Метод самосогласованного поля — метод, используемый в физике и химии, в котором состояние отдельной частицы сложной системы (кристалла, плазмы, раствора, атома, молекулы, атомного ядра и т. п.) определяется усреднённым полем, создаваемым всеми остальными частицами и зависящим от состояния каждой частицы. Тем самым состояние каждой из подсистем автоматически согласуется с состояниями всех остальных частей, с чем и связано название метода. Затем, вместо описания взаимодействия заряженных частиц в плазме посредством столкновений, предлагается использовать самосогласованное поле, созданное заряженными частицами плазмы. Для этого описания вводятся функции распределения электронов и (положительных) ионов плазмы. Вместо уравнения Больцмана Власов предлагает использовать следующую систему уравнений для описания заряженных компонент плазмы (электронов и положительных ионов): ДЕТАЛЬНОГО РАВНОВЕСИЯ ПРИНЦИП - общий принцип квантовой механики и статистич. физики, согласно к-рому для изолиров. системы вероятность прямого перехода nàm между квантовыми состояниями n и m равна вероятности обратного перехода màn
58. Свойства атомных ядер. Опыт Резерфорда. Размеры ядер. Ядро как совокупность протонов и нейтронов. Распределение заряда в ядре. Масса и энергия связи ядра. Энергия отделения нуклонов и кластеров от ядра. Спин ядра и моменты импульсов составляющих ядро нуклонов. Четность ядерных состояний. Изоспин нуклонов и ядер. Спектры ядер. Электромагнитные моменты ядра и нуклонов. Опыт Резерфорда. Известно, что две модели атома претендовали на правильное описание структуры атома. Модель Томсона – капельная модель и планетарная или ядерная модель – Модель Резерфорда. Задача поставленная Резерфордом, состояла в том, чтобы по угловому распределению альфа-частиц ответить на вопрос, как распределены масса и заряд атома. С этой целью золотая фольга толщиной в 1 мкм обстреливалась пучком альфа-частиц с энергией в несколько МэВ. Результаты опыта свести к двум важным пунктам:1) большая часть альфа-частиц отклоняется на малые углы, в среднем Выводы, сделанные Резерфордом, сегодня общеизвестны: вся масса атома практически целиком сосредоточена в положительно заряженном малом объеме, называемом ядром. Размер ядра на 4-5 порядком меньше размеров атома (размер атома Предполагается, что ядра атомов имеют форму шара, поэтому их размер выражают их радиусом. Согласно экспериментальным данным радиус ядра можно рассчитать по приближенной формуле: Ядро – центральная положительно заряженная часть атома. Ядро состоит из нуклонов, которые могут находиться в двух состояниях – протонном (протон имеет положительный заряд) и нейтронном (нейтрон нейтрален). Ядра состоят из четного/нечетного числа протонов и четного/нечетного числа нейтронов, называют четно-четными (нечетно-нечетными). Ядра состоящие из четного/нечетного числа протонов и нечетного/четного числа нейтронов, называют четно-нечетными (нечетно-четными). Иначе говоря, первое слово относится к протонам, второе – к нейтронам. Энергия связи ядра находится по формуле: Спином ядра называется максимальное значение проекции собственного момента импульсов выделенную ось. Полный момент количества движения нуклона в ядре складывается из его спина и орбитального момента относительно центра ядра: Изоспин ядра и нуклонов. Любое состояние ядер помимо энергии, спина и четности характеризуется квантовыми числами, которые называются изоиспином и проекцией изоспина. Введение этих квантовых чисел связано с тем фактом, что ядерные силы инвариантны относительно замены протонов на нейтроны. Это особенно ярко проявляется в спектрах ядер, т.е. ядер-изобар, у которых число протонов одного равно числу нейтронов другого (например Ci13, N13). Для всех известных пар таких ядер имеет место подобие спектров низких возбужденных состояний: спины и четности низших состояний одинаковы, а энергии возбуждения близки. С точки зрения теории изоспина, нейтрон и протон являются одной и той же частицей – нуклон с изоспином
Электромагнитные моменты определяют потенциал взаимодействия ядра или частиц с внешними электрическими и магнитными полями:
Квадрат волновой функции основного состояния ядра является четной функцией координат, z – нечетная функция. Интеграл по трехмерному пространству от произведения четной и нечетной функций всегда равен 0.
59. Модели атомных ядер. Модель заряженной жидкой капли. Формула Вайцзеккера. Модель оболочек. Физическое обоснование оболочечной модели ядра. Потенциал среднего ядерного поля. Спин-орбитальное взаимодействие. Одночастичные состояния в ядерном потенциале. Модель оболочек для средних и тяжелых ядер. Роль кулоновского взаимодействия. Модель коллективных ядерных колебаний. Вращательные спектры ядер. Капельная модель. В рамках этой модели, действующие между нуклонами, рассматривают как аналог молекулярных сил в капле жидкости. Энергия притяжения нуклонов, обусловленная ядерными силами, соответствует энергии молекулярного притяжения молекул в капле жидкости. Для того чтобы капельную модель использовать для вычисления энергии связи ядра необходимо дополнительно учесть кулоновское отталкивание положительно заряженных протонов. Силы межнуклонного взаимодействия короткодействующие, поэтому нуклоны, находятся на поверхности ядра, испытывают одностороннее притяжение ядерными силами внутри ядра, что характеризуется аналогом коэффициента поверхностного натяжения для жидкости. Кроме того, на величину энергии связи ядра влияет взаимная ориентация спинов отдельных нуклонов. Результатом расчета по капельной модели является полуэмпирическая формула Вейцзеккера для энергии связи нуклонов в ядре
Где коэффициенты имеют следующие численные значения:
Первое слагаемое (пропорциональное массовому числу) обусловлено короткодействующим характером межнуклонных сил. В результате основной вклад в энергию связи пропорционален числу нуклонов. Второй член учитывает то, что часть нуклонов находится на поверхности ядра. Как следствие энергия связи уменьшается за счет одностороннего притяжения поверхности ядра и, в соответствии с формулой Подсчеты по формуле Вейцзеккера показывают, что в случае легких ядер Оболочная модель. В модели ядерных оболочек нуклоны рассматриваются как независимые частицы в самосогласованном потенциале, создаваемом всей совокупностью нуклонов в ядре. Уровни энергии нуклонов где Потенциал прямоугольной потенциальной ямы: Основные положения одночастичной оболочечной модели Суммарный момент основного состояния четно-четного ядра (N и Z - четные числа) равен 0. Суммарный момент основных состояний ядер с нечетным A равен полному моменту j неспаренного нуклона.Правило хорошо выполняется для ядер, у которых сверх заполненного состояния есть еще один нуклон, либо для заполнения последнего состояния недостает одного нуклона. Недостающий нуклон называется дыркой и момент ядра определяется спином и четностью этого недостающего нуклона. Суммарный момент нечетно-нечетных ядер, неспаренные нуклоны которого находятся в одинаковых состояниях, равен удвоенному полному моменту неспаренного нуклона. Энергия уровня с данным n растет с ростом l. Спин орбитальное взаимодействие для параллельных
Радиоактивность Некоторое время атомное ядро и электроны считались элементарными составляющими вещества. Первое указание на существование атомного ядра связано с открытием в 1898 году А. Беккерелем радиоактивности. Это произошло задолго до того, как Резерфорд экспериментально доказал его существование. Оказалось, что некоторые минералы естественного происхождения самопроизвольно испускают излучение неизвестной природы. Нейтрально заряженных частиц - фотонов. Отрицательно заряженных частиц- электронов. Положительно заряженных частиц. Изучая треки образующихся при радиоактивном распаде положительно заряженных частиц в электрическом поле, Э. Резерфорд показал, что это частицы с массой атома гелия и зарядом +2e. В 1919 году Ф. Астон построил первый масс-спектрограф, с помощью которого были получены точные значения масс атомных ядер. Было доказано, что положительно заряженные частицы, обнаруженные при радиоактивном распаде ядер, являются ядрами атома гелия. Эти частицы были названы α-частицами. Альфа-распад - распад атомных ядер, сопровождающийся испусканием альфа-частиц (ядер 4He). В естественных условиях на Земле существует около 40 альфа-радиоактивных изотопов. Они объединены в три радиоактивных ряда, которые начинаются с 236U (232Th) (A = 4n), 238U (A = 4n + 2), 235U (A = 4n + 3). К ним можно с некоторой натяжкой, так как изотопы этого ряда успели распасться за время существования Земли, отнести четвертый ряд, который начинается c 237Np (A = 4n + 1). Способность ядер самопроизвольно распадаться, испуская частицы, называется радиоактивностью. Радиоактивный распад - статистический процесс. Каждое радиоактивное ядро может распасться в любой момент и закономерность наблюдается только в среднем, в случае распада достаточно большого количества ядер.
Проинтегрировав (1) получим закон радиоактивного распада
N0 - количество радиоактивных ядер в момент времени t = 0. Среднее время жизни τ –
Период полураспада T1/2 - время, за которое первоначальное количество радиоактивных ядер уменьшится в два раза
Активность A - среднее количество ядер, распадающихся в единицу времени
Активность измеряется в кюри (Ки) и беккерелях (Бк) Бета-распад - спонтанное превращение ядра (A,Z) в ядро-изобар (A,Z+1) в результате испускания лептонов (электрон и антинейтрино, позитрон и нейтрино), либо поглощения электрона с испусканием нейтри
|
||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 471; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.234.124 (0.016 с.) |

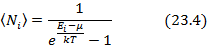
 — среднее число бозонов в квантовом состоянии с энергией
— среднее число бозонов в квантовом состоянии с энергией  ,
, 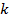 — постоянная Больцмана,
— постоянная Больцмана,  —термодинамическая температура, µ - химический потенциал; µ не зависит от энергии, а определяется только температурой и плотностью числа частиц. Химический потенциал находится обычно из условия, что сумма всех
—термодинамическая температура, µ - химический потенциал; µ не зависит от энергии, а определяется только температурой и плотностью числа частиц. Химический потенциал находится обычно из условия, что сумма всех  , так как иначе среднее число частиц в данном квантовом состоянии отрицательно, что не имеет физического смысла. Он определяет изменение внутренней энергии системы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внутренняя энергия (энтропия, объем), фиксированы.
, так как иначе среднее число частиц в данном квантовом состоянии отрицательно, что не имеет физического смысла. Он определяет изменение внутренней энергии системы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внутренняя энергия (энтропия, объем), фиксированы.
 — химический потенциал. В отличие от (23.4)
— химический потенциал. В отличие от (23.4)  , то распределения Бозе — Эйнштейна (23.4) и Ферми — Дирака (23.5) переходят в классич-кое распределение Максвелла-Больцмана:
, то распределения Бозе — Эйнштейна (23.4) и Ферми — Дирака (23.5) переходят в классич-кое распределение Максвелла-Больцмана:
 , т. е. при малой степени вырождения, распределения Бозе — Эйнштейна (23.4) и Ферми — Дирака (23.5) переходят в классическое распределение Максвелла — Больцмана (23.6).
, т. е. при малой степени вырождения, распределения Бозе — Эйнштейна (23.4) и Ферми — Дирака (23.5) переходят в классическое распределение Максвелла — Больцмана (23.6). называется температура, ниже которой
называется температура, ниже которой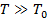 , то поведение системы частиц (газа) описывается классическими законами.
, то поведение системы частиц (газа) описывается классическими законами. в пределе Т - >0 обращается в «ступенчатую» функцию: единица ПРИ ε < μ и
в пределе Т - >0 обращается в «ступенчатую» функцию: единица ПРИ ε < μ и 
 , ω- излучение частоты,
, ω- излучение частоты,  - объемная концентрация.
- объемная концентрация.
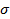 - постоянная Стефана- Больцмана, а
- постоянная Стефана- Больцмана, а  - скорость света в вакууме.
- скорость света в вакууме. т.к.полная вероятность обнаружить систему в водном из допустимых значений равна единице, то ВФ принадлежит к классу нормируемых
т.к.полная вероятность обнаружить систему в водном из допустимых значений равна единице, то ВФ принадлежит к классу нормируемых  . Каждой динамической величине ставиться F(q,p) определяемой в классической теории как функция координат и импульсов всех частиц, в кв.мех ставиться в соответсвие самосопряженный оператор
. Каждой динамической величине ставиться F(q,p) определяемой в классической теории как функция координат и импульсов всех частиц, в кв.мех ставиться в соответсвие самосопряженный оператор  Б) микроскопическое состояние можно задать как смешанное механическое состояние. Наблюдаемые величины в данном случае определяются как средние от квантомеханических средних(для каждого чистого состояния n величина F принимает значение
Б) микроскопическое состояние можно задать как смешанное механическое состояние. Наблюдаемые величины в данном случае определяются как средние от квантомеханических средних(для каждого чистого состояния n величина F принимает значение  , а каждое состояние n входит с вероятностным весом
, а каждое состояние n входит с вероятностным весом  )
)  , Предположим, что мы наблюдаем в течение весьма длительного промежутка времени некоторую подсистему. Разделим этот промежуток времени на очень большое (в пределе—бесконечное) количество одинаковых малых интервалов, разделенных моментами времени t1, tJ... В каждый из этих моментов рассматриваемая подсистема изобразится в ее фазовом пространстве точкой (назовем эти точки А1, А2, А3,...)• Совокупность полученных точек распределится в фазовом пространстве с плотностью, в пределе пропорциональной в каждом данном месте значению функции распределения ρ(р, q) по самому смыслу последней, как определяющей вероятности различных состояний подсистемы. Рассмотрим одновременно очень большое (в пределе—бесконечное) число совершенно одинаковым образом устроенных подсистем), находящихся в некоторый момент времени t = 0 в состояниях, изображающихся точками
, Предположим, что мы наблюдаем в течение весьма длительного промежутка времени некоторую подсистему. Разделим этот промежуток времени на очень большое (в пределе—бесконечное) количество одинаковых малых интервалов, разделенных моментами времени t1, tJ... В каждый из этих моментов рассматриваемая подсистема изобразится в ее фазовом пространстве точкой (назовем эти точки А1, А2, А3,...)• Совокупность полученных точек распределится в фазовом пространстве с плотностью, в пределе пропорциональной в каждом данном месте значению функции распределения ρ(р, q) по самому смыслу последней, как определяющей вероятности различных состояний подсистемы. Рассмотрим одновременно очень большое (в пределе—бесконечное) число совершенно одинаковым образом устроенных подсистем), находящихся в некоторый момент времени t = 0 в состояниях, изображающихся точками В данном случае «координатами» х являются координаты q и импульсы р, а «скоростями»
В данном случае «координатами» х являются координаты q и импульсы р, а «скоростями»  — производные по времени q и р, определяемые уравнениями механики. Таким образом, имеем:
— производные по времени q и р, определяемые уравнениями механики. Таким образом, имеем: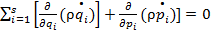 Раскрывая производные, пишем:
Раскрывая производные, пишем:  ,Написав уравнения механики в форме Гамильтона
,Написав уравнения механики в форме Гамильтона ,
, 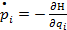 где Н = Н(р, q) —функция Гамильтона рассматриваемой подси стемы, мы видим, что
где Н = Н(р, q) —функция Гамильтона рассматриваемой подси стемы, мы видим, что 
 . Мы приходим, следовательно, к существенному выводу, что функция распределения постоянна вдоль фазовых траекторий подсистемы (так называемая теорема Лиувилля); напомним, что поскольку мы говорим о квазизамкнутых подсистемах, то полученный результат справедлив лишь для не слишком больших промежутков времени, в течение которых подсистема с достаточной точностью ведет себя как замкнутая. Исходным моментом для построения системы уравнений для функции
. Мы приходим, следовательно, к существенному выводу, что функция распределения постоянна вдоль фазовых траекторий подсистемы (так называемая теорема Лиувилля); напомним, что поскольку мы говорим о квазизамкнутых подсистемах, то полученный результат справедлив лишь для не слишком больших промежутков времени, в течение которых подсистема с достаточной точностью ведет себя как замкнутая. Исходным моментом для построения системы уравнений для функции  является диф.ур для ω(r1,r2….rn). т.к. все частицы в рассматриваемом случае одинаковы, то дифференцируя экспоненцальную функцию получим
является диф.ур для ω(r1,r2….rn). т.к. все частицы в рассматриваемом случае одинаковы, то дифференцируя экспоненцальную функцию получим 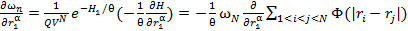 в пространственно однородном случае одночастичная функция
в пространственно однородном случае одночастичная функция  , поэтому будем выводить второе уравнение
, поэтому будем выводить второе уравнение Желая получить уравнение
Желая получить уравнение  мы должны умножить исходное уравнение на
мы должны умножить исходное уравнение на  и проинтегрировать по переменным r. Тогда производя расчеты аналогичные первым получим
и проинтегрировать по переменным r. Тогда производя расчеты аналогичные первым получим 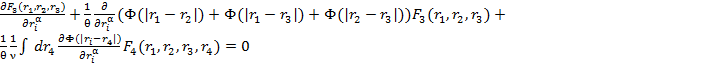
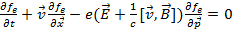 ;
;  ;
;  ;
;  ;
; 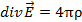 ;
;  ;
; 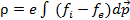 ;
;  Здесь e — заряд электрона, c — скорость света,
Здесь e — заряд электрона, c — скорость света,  и
и  — самосогласованное электрическое и магнитное поле, созданные в точке в момент времени t всеми заряженными частицами плазмы. Существенное отличие этой системы уравнений от уравнений движения заряженных частиц во внешнем электромагнитном поле в том, что само самосогласованное электромагнитное поле сложным образом зависит от функций распределения ионов и электронов. Затухания Ландау- бесстолкновительное затухание колебаний и волн в плазме. Космич. плазму во многих случаях можно считать бесстолкновительной в том смысле, что ср. время между соударениями намного превышает характерные времена происходящих в ней процессов, а длина свободного пробега частиц больше размеров, на к-рых развиваются эти процессы. В качестве примеров такой бесстолкновительной плазмы можно назвать магнитосферную плазму, плазму солнечного ветра, плазму пульсаров и т.д. Для бесстолкновительной плазмы доминирующим явл. коллективное взаимодействие волн и частиц, приводящее, в частности, к затуханию или возбуждению эл.-магн. волн. Наиболее простое и вместе с тем важное явление в коллективных взаимодействиях - резонансное взаимодействие волн и частиц. Классич. пример такого взаимодействия - Л. з. ленгмюровских колебаний в плазме без магн. поля.
— самосогласованное электрическое и магнитное поле, созданные в точке в момент времени t всеми заряженными частицами плазмы. Существенное отличие этой системы уравнений от уравнений движения заряженных частиц во внешнем электромагнитном поле в том, что само самосогласованное электромагнитное поле сложным образом зависит от функций распределения ионов и электронов. Затухания Ландау- бесстолкновительное затухание колебаний и волн в плазме. Космич. плазму во многих случаях можно считать бесстолкновительной в том смысле, что ср. время между соударениями намного превышает характерные времена происходящих в ней процессов, а длина свободного пробега частиц больше размеров, на к-рых развиваются эти процессы. В качестве примеров такой бесстолкновительной плазмы можно назвать магнитосферную плазму, плазму солнечного ветра, плазму пульсаров и т.д. Для бесстолкновительной плазмы доминирующим явл. коллективное взаимодействие волн и частиц, приводящее, в частности, к затуханию или возбуждению эл.-магн. волн. Наиболее простое и вместе с тем важное явление в коллективных взаимодействиях - резонансное взаимодействие волн и частиц. Классич. пример такого взаимодействия - Л. з. ленгмюровских колебаний в плазме без магн. поля.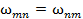 , Д. р. п. является следствием осн. принципов квантовой механики, в частности симметрии квантовых ур-ний движения относительно обращения времени. Если квантовая система взаимодействует с другой большой системой (термостатом), то, согласно Д. р. п.,
, Д. р. п. является следствием осн. принципов квантовой механики, в частности симметрии квантовых ур-ний движения относительно обращения времени. Если квантовая система взаимодействует с другой большой системой (термостатом), то, согласно Д. р. п.,  где
где  -где -энергии состояний n и m.В случае, когда состояния п и т вырождены или уровни расположены очень плотно, так что вычисляется вероятность перехода между состояниями в элементах фазового объёма, то, согласно Д. р. п., равны вероятности перехода, отнесённые к одному конечному состоянию:
-где -энергии состояний n и m.В случае, когда состояния п и т вырождены или уровни расположены очень плотно, так что вычисляется вероятность перехода между состояниями в элементах фазового объёма, то, согласно Д. р. п., равны вероятности перехода, отнесённые к одному конечному состоянию: где
где  -плотности состояний с энергией em,en.
-плотности состояний с энергией em,en. и распределение по углам этих частиц соответствовало нормальному закону, 2)некоторое число частиц отклонялось на большие углы, а отдельные частицы изредка рассеивались даже на углы, близкие к
и распределение по углам этих частиц соответствовало нормальному закону, 2)некоторое число частиц отклонялось на большие углы, а отдельные частицы изредка рассеивались даже на углы, близкие к  .
. см), которые, по мнению Резерфорда, представляют собой систему электронов, двигающихся вокруг ядра наподобие планет вокруг Солнца. Протоны и нейтроны образуют атомные ядра всех химических элементов. При описании атомных ядер используют обозначения Z – число протонов, N – число нейтронов, A=Z+N (массовое число). Ядра с одинаковыми Z называются изотопами, с одинаковым A – изобарами.
см), которые, по мнению Резерфорда, представляют собой систему электронов, двигающихся вокруг ядра наподобие планет вокруг Солнца. Протоны и нейтроны образуют атомные ядра всех химических элементов. При описании атомных ядер используют обозначения Z – число протонов, N – число нейтронов, A=Z+N (массовое число). Ядра с одинаковыми Z называются изотопами, с одинаковым A – изобарами. . Значение
. Значение  метра используют для измерения ядерных расстояний и называют ферми.
метра используют для измерения ядерных расстояний и называют ферми. где
где  - масса протонов, нейтронов и ядра. Энергия связи ядра показывает, какое минимальное количество энергии нужно затратить чтобы разделить ядро на протоны и нейтроны.
- масса протонов, нейтронов и ядра. Энергия связи ядра показывает, какое минимальное количество энергии нужно затратить чтобы разделить ядро на протоны и нейтроны.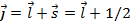 . Спин ядра – результат сложения моментов нуклонов ядра:
. Спин ядра – результат сложения моментов нуклонов ядра:  . Для спинов атомных ядер экспериментально установлены следующие закономерности: если A – четное, то
. Для спинов атомных ядер экспериментально установлены следующие закономерности: если A – четное, то  , т.е. спин ядра имеет целочисленное значение; если A – нечетное, то
, т.е. спин ядра имеет целочисленное значение; если A – нечетное, то  , т.е. спин ядра имеет полуцелое значение; четно-четные ядра в основном состоянии имеют значение спина
, т.е. спин ядра имеет полуцелое значение; четно-четные ядра в основном состоянии имеют значение спина  , что указывает на взаимную компенсацию моментов нуклонов в основном состоянии ядра – особое свойство межнуклонного взаимодействия.
, что указывает на взаимную компенсацию моментов нуклонов в основном состоянии ядра – особое свойство межнуклонного взаимодействия.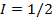 - в двух разных состояниях, различающихся проекцией изоспина на выделенную ось в пространстве изоспина. Таких проекций для
- в двух разных состояниях, различающихся проекцией изоспина на выделенную ось в пространстве изоспина. Таких проекций для  (протон) и
(протон) и  (нейтрон). Пространство изоспина не совпадает с обычным координатным пространством. Система Z протонов и N нейтронов – ядро – имеет проекцию изоспина
(нейтрон). Пространство изоспина не совпадает с обычным координатным пространством. Система Z протонов и N нейтронов – ядро – имеет проекцию изоспина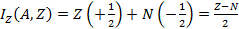 Изоспин системы нуклонов является векторной суммой изоспинов составляющих:
Изоспин системы нуклонов является векторной суммой изоспинов составляющих:  . Ядерные взаимодействия не зависят от проекции изоспина, или сильные взаимодействия инвариантны относительно вращений в изоспиновом пространстве. Ядерные силы зависят от величины изоспина. Низшим по энергии состояниям системы нуклонов, т.е. основным состоянием ядер, является состояние с низшим возможным значение изоспина, которое равно:
. Ядерные взаимодействия не зависят от проекции изоспина, или сильные взаимодействия инвариантны относительно вращений в изоспиновом пространстве. Ядерные силы зависят от величины изоспина. Низшим по энергии состояниям системы нуклонов, т.е. основным состоянием ядер, является состояние с низшим возможным значение изоспина, которое равно:  . Взбужденные состояния ядер могут иметь более высокие значения изоспина, но с той же проекцией. Таким образом, характеристиками уровней данного ядра являются энергия, спин состояния, четность состояния и изоспин.
. Взбужденные состояния ядер могут иметь более высокие значения изоспина, но с той же проекцией. Таким образом, характеристиками уровней данного ядра являются энергия, спин состояния, четность состояния и изоспин. . Здесь
. Здесь  - заряд ядра, D – электрический дипольный момент ядра,
- заряд ядра, D – электрический дипольный момент ядра,  - квадрупольный момент ядра,
- квадрупольный момент ядра,  - магнитный дипольный момент. Более высокие по тензорной размерности члены потенциала взаимодействия дают пренебрежимо малый вклад во взаимодействие. Электрический дипольный момент ядер – в основном состоянии равен нулю. Равенство нулю момента
- магнитный дипольный момент. Более высокие по тензорной размерности члены потенциала взаимодействия дают пренебрежимо малый вклад во взаимодействие. Электрический дипольный момент ядер – в основном состоянии равен нулю. Равенство нулю момента  является следствием четности квадрата волновой функции основного состояния ядра:
является следствием четности квадрата волновой функции основного состояния ядра:
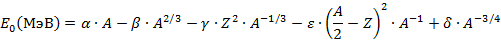




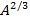 . Треть слагаемое представляет собой энергию кулоновского отталкивания протонов, пропорциональную
. Треть слагаемое представляет собой энергию кулоновского отталкивания протонов, пропорциональную  или, согласно формуле,
или, согласно формуле,  . Четвертый член обусловлен обменным характером ядерных сил и характеризует увеличение энергии связи при равенстве числа протонов и нейтронов в ядре
. Четвертый член обусловлен обменным характером ядерных сил и характеризует увеличение энергии связи при равенстве числа протонов и нейтронов в ядре  . Последнее слагаемое возникает из-за зависимости межнуклонных сил от взаимной ориентации спинов протонов и нейтронов. Как следствие, устойчивость атомных ядер убывает в последовательности: четно-четные, четно-нечетные (нечетно-четные), нечетно-нечетные ядра.
. Последнее слагаемое возникает из-за зависимости межнуклонных сил от взаимной ориентации спинов протонов и нейтронов. Как следствие, устойчивость атомных ядер убывает в последовательности: четно-четные, четно-нечетные (нечетно-четные), нечетно-нечетные ядра. , максимум энергии связи достигается при равенстве числа протонов и нейтронов
, максимум энергии связи достигается при равенстве числа протонов и нейтронов 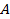 (из-за квадратичной зависимости третьего члена от числа протонов) максимум энергии связи двигается в область
(из-за квадратичной зависимости третьего члена от числа протонов) максимум энергии связи двигается в область  . Иначе говоря, в тяжелых ядрах относительное количество нейтронов в ядре увеличивается с ростом номера химического элемента.
. Иначе говоря, в тяжелых ядрах относительное количество нейтронов в ядре увеличивается с ростом номера химического элемента.
 - волновая функция нуклона я энергией
- волновая функция нуклона я энергией  - оператор Гамильтона,
- оператор Гамильтона,  - операторы кинетической и потенциальной энергии. В простейших моделях сферических ядер потенциал
- операторы кинетической и потенциальной энергии. В простейших моделях сферических ядер потенциал 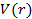 выбирают в виде потенциала трехмерного гармонического осциллятора, либо прямоугольной потенциальной ямы.
выбирают в виде потенциала трехмерного гармонического осциллятора, либо прямоугольной потенциальной ямы.  ; где –
; где –  - осцилляторная частота.
- осцилляторная частота. . Потенциал Вудса-Саксона:
. Потенциал Вудса-Саксона:  ; где
; где  - глубина потенциала,
- глубина потенциала, 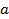 - параметр характеризующий диффузность (размытие) края потенциала. Потенциал Вудса-Саксона представляет нечто среднее между осцилляторным потенциалом и потенциалом прямоугольной ямы. В потенциале Вудса-Саксона снимаются вырождения, свойственные гармоническому осциллятору. Однако реалистический потенциал Вудса-Саксона, также как и осцилляторный потенциал, не в состоянии объяснить наблюдаемые в эксперименте магические числа нуклонов. Решение проблемы было найдено М. Гепперт-Майер и Дж. Иенсеном, которые добавили к центрально-симметричному потенциалу
- параметр характеризующий диффузность (размытие) края потенциала. Потенциал Вудса-Саксона представляет нечто среднее между осцилляторным потенциалом и потенциалом прямоугольной ямы. В потенциале Вудса-Саксона снимаются вырождения, свойственные гармоническому осциллятору. Однако реалистический потенциал Вудса-Саксона, также как и осцилляторный потенциал, не в состоянии объяснить наблюдаемые в эксперименте магические числа нуклонов. Решение проблемы было найдено М. Гепперт-Майер и Дж. Иенсеном, которые добавили к центрально-симметричному потенциалу 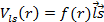 . Спин-орбитальное взаимодействие приводит к расщеплению уровня с данным значением l на два состояния 1+1/2 и 1-1/2. При этом состояние с l + 1/2 смещается вниз по энергии, а состояние с l - 1/2 - вверх. Величина спин-орбитального расщепления уровней пропорциональна величине орбитального момента l. Поэто уровни с большими значениями орбитального момента l > 3 сильно смещаясь вниз по энергии оказываются среди уровней предыдущей оболочки, что позволяет правильно воспроизвести магические числа. Для протонов в самосогласованый потенциал должен быть включен также кулоновский потенциал. Cостояния нуклонов характеризуются квантовыми числами, которые определяют физические величины, сохраняющиеся при движении в сферически-симметричном поле. В оболочечной модели спин ядра складывается из суммы спинов и орбитальных моментов отдельных нуклонов. Принцип Паули и специфика ядерного взаимодействия приводят к тому, что все четно-четные ядра имеют полный момент (спин) равный 0. Четность ядерного состояния определяется произведением внутренних четностей нуклонов на четности волновых функций, описывающих движение нуклонов относительно общего центра инерции. Внутренняя четность нуклонов принята положительной. При расчете нейтронных одночастичных состояний с потенциалом Вудса-Саксона, с небольшой зависимостью его глубины от нейтронного избытка, видно что радиус ядерного потенциала пропорционален
. Спин-орбитальное взаимодействие приводит к расщеплению уровня с данным значением l на два состояния 1+1/2 и 1-1/2. При этом состояние с l + 1/2 смещается вниз по энергии, а состояние с l - 1/2 - вверх. Величина спин-орбитального расщепления уровней пропорциональна величине орбитального момента l. Поэто уровни с большими значениями орбитального момента l > 3 сильно смещаясь вниз по энергии оказываются среди уровней предыдущей оболочки, что позволяет правильно воспроизвести магические числа. Для протонов в самосогласованый потенциал должен быть включен также кулоновский потенциал. Cостояния нуклонов характеризуются квантовыми числами, которые определяют физические величины, сохраняющиеся при движении в сферически-симметричном поле. В оболочечной модели спин ядра складывается из суммы спинов и орбитальных моментов отдельных нуклонов. Принцип Паули и специфика ядерного взаимодействия приводят к тому, что все четно-четные ядра имеют полный момент (спин) равный 0. Четность ядерного состояния определяется произведением внутренних четностей нуклонов на четности волновых функций, описывающих движение нуклонов относительно общего центра инерции. Внутренняя четность нуклонов принята положительной. При расчете нейтронных одночастичных состояний с потенциалом Вудса-Саксона, с небольшой зависимостью его глубины от нейтронного избытка, видно что радиус ядерного потенциала пропорционален 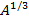 . Это приводит к тому, что с ростом A уменьшается расстояние между одночастичными состояниями. Кроме увеличения плотности одночастичных состояний с ростом A, видно, что меняется последовательность состояний. Плотность одночастичных протонных состояний больше чем нейтронных, а их последовательность для оболочек выше четвертой иная, что обусловленно дополнительным вкладом кулоновского потенциала.
. Это приводит к тому, что с ростом A уменьшается расстояние между одночастичными состояниями. Кроме увеличения плотности одночастичных состояний с ростом A, видно, что меняется последовательность состояний. Плотность одночастичных протонных состояний больше чем нейтронных, а их последовательность для оболочек выше четвертой иная, что обусловленно дополнительным вкладом кулоновского потенциала. и
и 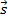 больше, чем для антипараллельных.
больше, чем для антипараллельных. =
=