
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели в механике. Система отсчета. Траектория, длина пути, вектор перемещенияСтр 1 из 9Следующая ⇒
Е.В. Метелкин
КУРС ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ «Физика»
Учебное пособие
Москва 2016 г.
Рецензенты: Акатьев В.А. – доктор технических наук, профессор, профессор кафедры Техносферной безопасности и экологии Российского государственного социального университета
Рязанов А.И. – доктор физ.-мат. наук, профессор, зав. лаб., Национальный исследовательский центр «Курчатовский институт», (НИЦ КИ)
Метелкин Е.В. Курс лекций по дисциплине «Физика»: учебное пособие. Содержание учебного пособия Курс лекций по дисциплине «Физика» соответствует разделам и темам, указанным в программе курса для студентов высших учебных заведений социального профиля. Курс основывается на учебнике: Трофимова Т.И Курс физики. – М.: Академия, 2009г.
Рекомендовано в качестве учебного пособия на заседании кафедры Техносферной безопасности и экологии Российского государственного социального университета (Протокол № 5 от 25 ноября 2015 г.).
Содержание Введение………………………………………………………………………………….7 Раздел 1. Физические основы механики……………………………………………….9. Глава 1. Элементы кинематики…………………………………………………9 § 1. Модели в механике. Система отсчета. Траектория, длина пути, вектор перемещения………………………………………………………9 § 2. Скорость……………………………………………………………………..11 § 3. Ускорение и его составляющие……………………………………………12 § 4. Угловая скорость и угловое ускорение……………………………………14
Глава 2. Динамика материальной точки и поступательного движения твердого тела………………………………………………………………………17 § 5. Первый закон Ньютона………………………………………………………17 § 6. Второй закон Ньютона……………………………………………………….17 § 7. Третий закон Ньютона……………………………………………………….20 § 8. Силы трения…………………………………………………………………..20 § 9. Закон сохранения импульса. Центр масс…………………………………...21
Глава 3. Работа и энергия………………………………………………………...23 § 10. Энергия, работа, мощность…………………………………………………23 § 11. Кинетическая и потенциальная энергия…………………………………..25 § 12. Закон сохранения энергии………………………………………………… 27
§ 13. Графическое представление энергии………………………………………28 § 14. Удар абсолютно упругих и неупругих тел………………………………...30
Глава 4. Механика твердого тела…………………………………………………34 § 15. Момент инерции…………………………………………………………….34 § 16. Кинетическая энергия вращения……………………………………………35 § 17. Момент силы. Уравнение динамики вращательного движения твердого тела……………………………………………………………………….36 § 18. Момент импульса и закон его сохранения…………………………………37 § 19. Свободные оси. Гироскоп……………………………………………………40 § 20. Деформации твердого тела…………………………………………………..42
Глава5. Тяготение. Элементы теории поля……………………………………….44 § 21. Законы Кеплера. Закон всемирного тяготения……………………………..44 § 22. Сила тяжести и вес. Невесомость……………………………………………46 § 23. Поле тяготения и его напряженность………………………………………..47 § 24. Работа в поле тяготения. Потенциал поля тяготения……………………….47 § 25. Космические скорости………………………………………………………...49 § 26. Неинерциальные системы отсчета. Силы инерции…………………………50 . Глава 6. Элементы механики жидкостей…………………………………………..54 § 27. Давление в жидкости и газе…………………………………………………...54 § 28. Уравнение неразрывности…………………………………………………….55 § 29. Уравнение Бернулли и следствия из него……………………………………56 § 30. Вязкость (внутреннее трение). Ламинарный и турбулентный режимы течения жидкости…………………………………………………………..59 § 31. Методы определения вязкости………………………………………………...61 § 32. Движение тел в жидкостях и газах…………………………………………….62 Раздел 2. Основы молекулярной физики и термодинамики……………………………….64 Глава 7. Молекулярно-кинетическая теория идеальных газов…………………….64 § 33. Статистический и термодинамический методы. Опытные законы идеальных газов…………………………………………………………………………………….64 § 34. Уравнение Клапейрона-Менделеева……………………………………………67 § 35. Основное уравнение молекулярно-кинетической теории идеальных газов……………………………………………………………………………………68
§ 36. Закон Максвелла о распределении молекул идеального газа по скоростям и энергиям теплового движения……………………………………………………70 § 37. Барометрическая формула. Распределение Больцмана…………………….72 §38. Средне число столкновений и средняя длина свободного пробега молекул………………………………………………………………………………74 § 39. Опытное обоснование молекулярно-кинетической теории………………..75 § 40. Явления переноса в термодинамически неравновесных системах…………76
Глава 8. Основы термодинамики……………………………………………………79 § 41. Число степеней свободы молекулы. Закон равномерного распределения энергии по степеням свободы молекул……………………………79 § 42. Первое начало термодинамики………………………………………………...80 § 43. Работа газа при изменении его объема………………………………………...81 § 44. Теплоемкость…………………………………………………………………….82 § 45. Применение первого начала термодинамики к изопроцессам……………….84 § 46. Адиабатический процесс. Политропный процесс…………………………….85 § 47. Круговой процесс (цикл). Обратимые и необратимые процессы………………………………………………………………………………..88 § 48. Энтропия, ее статистическое толкование и связь с термодинамической вероятностью……………………………………………………89 § 49. Второе начало термодинамики………………………………………………….91 § 50. Тепловые двигатели и тепловые машины. Цикл Карно и его КПД для идеального газа………………………………………………………….92
Раздел 3. Электричество и электромагнетизм……………………………………………….96
Глава 9. Электростатика………………………………………………………………96 § 51. Закон сохранения электрического заряда………………………………………96 § 52. Закон Кулона……………………………………………………………………..97 § 53. Электростатическое поле. Напряженность электростатического поля………97 § 54. Принцип суперпозиции электростатических полей. Поле диполя…………..100 § 55. Теорема Гаусса для электростатического поля в вакууме……………………102 § 56. Применение теоремы Гаусса к расчету некоторых электростатических полей в вакууме………………………………………………………………………103 § 57. Циркуляция вектора напряженности электростатического поля…………...106 § 58. Потенциал электростатического поля…………………………………………107 § 59. Напряженность как градиент потенциала. Эквипотенциальные поверхности……………………………………………………………………………109 § 60. Вычисление разности потенциалов по напряженности поля………………...110 § 61. Типы диэлектриков. Поляризация диэлектриков……………………………..111 § 62. Поляризованность. Напряженность поля в диэлектрике……………………..112 § 63. Электрическое смещение. Теореме Гаусса для электростатического поля в диэлектрике……………………………………………………………………114 § 64. Условия на границе раздела двух диэлектрических сред…………………….115 § 65. Сегнетоэлектрики……………………………………………………………….116 § 66. Проводники в электрическом поле…………………………………………….118 § 67. Электрическая емкость уединенного проводника……………………………120 § 68. Конденсаторы……………………………………………………………………121 § 69. Энергия системы зарядов, уединенного проводника и конденсатора. Энергия электростатического поля………………………………………………….123
Глава 10. Постоянный электрический ток…………………………………………..125 § 70. Электрический ток, сила и плотность тока……………………………………125 § 71. Сторонние силы. Электродвижущая сила и напряжение…………………….126 § 72. Закон Ома. Сопротивление проводников……………………………………..128 § 73. Работа и мощность тока. Закон Джоуля-Ленца………………………………129 § 74. Закон Ома для неоднородного участка цепи………………………………….130 § 75. Правила Кирхгофа для разветвленных цепей…………………………………131
Глава 11. Магнитное поле……………………………………………………………134 § 76. Магнитное поле и его характеристики………………………………………..134 § 77. Закон Био-Савара-Лапласа и его применение к расчету магнитного поля………………………………………………………………………136 § 78. Закон Ампера. Взаимодействие параллельных токов………………………..138 § 79. Магнитная постоянная. Единицы магнитной индукции и напряженности магнитного поля…………………………………………………….139 § 80. Магнитное поле движущегося заряда………………………………………….140 § 81. Действие магнитного поля на движущийся заряд……………………………141 § 82. Движение заряженных частиц в магнитном поле……………………………142 § 83. Ускорители заряженных частиц………………………………………………143 § 84. Эффект Холла…………………………………………………………………..145 § 85. Циркуляция вектора B магнитного поля в вакууме………………………….146 § 86. Магнитные поля соленоида и тороида………………………………………147 § 87. Поток вектора магнитной индукции. Теорема Гаусса для поля B …………………………………………………………………………….148 § 88. Работа по перемещению проводника и контура с током в магнитном поле…………………………………………………………………….149
Глава 12. Электромагнитная индукция…………………………………………….150 § 89. Явление электромагнитной индукции (опыты Фарадея)……………………150 § 90. Закон Фарадея и его вывод из закона сохранения энергии…………………151 § 91. Вращение рамки в магнитном поле…………………………………………..153 § 92. Вихревые токи (токи Фуко)…………………………………………………...154 § 93. Индуктивность контура. Самоиндукция…………………………………….155 § 94. Токи при размыкании и замыкании цепи……………………………………156 § 95. Взаимная индукция……………………………………………………………157 § 96. Трансформаторы……………………………………………………………….159 § 97. Энергия магнитного поля…………………………………………………….160
Глава 13 Магнитные свойства вещества………………………………………….161 § 98. Магнитные моменты электронов и атомов…………………………………161 § 99. Диа- и парамагнетизм………………………………………………………...163 § 100. Намагниченность. Магнитное поле в веществе……………………………164 § 101. Условия на границе раздела двух магнетиков…………………………….167 § 102. Ферромагнетики и их свойства……………………………………………..168 § 103. Природа ферромагнетизма………………………………………………….170
Глава 14. Основы теории Максвелла для электромагнитного поля…………….171 § 104. Вихревое электрическое поле………………………………………………171 § 105. Ток смещения………………………………………………………………..172 § 106. Уравнения Максвелла для электромагнитного поля……………………...175
Введение Предмет физики и ее связь с другими науками Окружающий вас мир, все существующее вокруг вас и обнаруживаемое нами посредством ощущений представляет собой материю. Неотъемлемым свойством материи и формой ее существования является движение. Движение в широком смысле слова — это всевозможные изменения материи — от простого перемещения до сложнейших процессов мышления. Разнообразные формы движения материи изучаются различными науками, в том числе и физикой. Предмет физики, как, впрочем, и любой науки, может быть раскрыт только по мере его детального изложения. Дать строгое определение предмета физики довольно сложно, потому что границы между физикой и рядом смежных дисциплин условны. На данной стадии развития нельзя сохранить определение физики только как науки о природе. Академик А. Ф. Иоффе (1880—1960; российский физик) определил физику как науку, изучающую общие свойства и законы движения вещества и поля. В настоящее время общепризнано, что вес взаимодействия осуществляются посредством полей, например гравитационных, электромагнитных, полей ядерных сил. Поле наряду с веществом является одной из форм существования материи. Неразрывная связь поля и вещества, а также различие в их свойствах будут рассмотрены по мере изучения курса. Физика — наука о наиболее простых и вместе с тем наиболее общих формах движения материи и их взаимных превращениях. Изучаемые физикой формы движения материи (механическая, тепловая и др.) присутствуют во всех высших и более сложных формах движения материи (химических, биологических и др.). Поэтому они, будучи наиболее простыми, являются в то же время наиболее общими формами движения материи. Высшие и более сложные формы движения материи — предмет изучения других наук (химии, биологии и др.). Физика тесно связана с естественными науками. Эта теснейшая связь физики с другими отраслями естествознания, как отмечал академик С. И. Вавилов (1891—1955; российский физик и общественный деятель), привела к тому, что физика глубочайшими корнями вросла в астрономию, геологию, химию, биологию и другие естественные науки. В результате образовался ряд новых смежных дисциплин, таких, как астрофизика, биофизика и др.
Физика тесно связана и с техникой, причем эта связь имеет двусторонний характер. Физика выросла из потребностей техники (развитие механики у древних греков, например, было вызвано запросами строительной и военной техники того времени), и техника, в свою очередь, определяет направление физических исследований (например, в свое время задача создания наиболее экономичных тепловых двигателей вызвала бурное развитие термодинамики). С другой стороны, от развития физики зависит технический уровень производства. Физика — база для создания новых отраслей техники (электронная техника, ядерная техника и др.). Бурный темп развития физики, растущие связи ее с техникой указывают на значительную роль курса физики во втузе: это фундаментальная база для теоретической подготовки инженера, без которой его успешная деятельность невозможна. Единицы физических величин Основным методом исследования в физике является опит — основанное на практике чувственно-эмпирическое познание объективной действительности, т. е. наблюдение исследуемых явлений в точно учитываемых условиях, позволяющих следить за ходом явлений и многократно воспроизводить его при повторении этих условий. Для объяснения экспериментальных фактов выдвигаются гипотезы. Гипотеза — это научное предположение, выдвигаемое для объяснения какого-либо явления и требующее проверки на опыте и теоретического обоснования для того, чтобы стать достоверной научной теорией. В результате обобщения экспериментальных фактов, а также результатов деятельности людей устанавливаются физические законы — устойчивые повторяющиеся объективные закономерности, существующие в природе. Наиболее важные законы устанавливают связь между физическими величинами, для чего необходимо эти величины измерять. Измерение физической величины есть действие, выполняемое с помощью средств измерений для нахождения значения физической величины в принятых единицах. Единицы физических величин можно выбрать произвольно, но тогда возникнут трудности при их сравнении. Поэтому целесообразно ввести систему единиц, охватывающую единицы всех физических величин. Для построения системы единиц произвольно выбирают единицы для нескольких не зависящих друг от друга физических величии. Эти единицы называются основными. Остальные же величины и их единицы выводятся из законов, связывающих эти величины и их единицы с основными. Они называются производными. В настоящее время обязательна к применению в научной, а также в учебной литературе Система Интернациональная (СИ), которая строится на семи основных единицах — метр, килограмм, секунда, ампер, кельвин, моль, кандела — и двух дополнительных — радиан и стерадиан. Метр (м) — длина пути, проходимого светом в вакууме за 1/299792458 с. Килограмм (кг) — масса, равная массе международного прототипа килограмма (платиноиридиевого цилиндра, хранящегося в Международном бюро мер и весов в Севре, близ Парижа). Секунда (с) — время, равное 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. Ампер (А) — сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, создаст между этими проводниками силу, равную 2×10–7 Н на каждый метр длины. Кельвин (К) — 1/273,16 часть термодинамической температуры тройной точки воды. Моль (моль) — количество вещества системы, содержащей столько же структурных элементов, сколько атомов содержится в нуклиде 12С массой 0,012 кг. Кандела (кд) — сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540×1012 Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср. Радиан (рад) — угол между двумя радиусами окружности, длина дуги между которыми равна радиусу. Стерадиан (ср) — телесный угол с вершиной в центре сферы, вырезающий на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы. Для установления производных единиц используют физические законы, связывающие их с основными единицами. Например, из формулы равномерного прямолинейного движения v=s/t (s – пройденный путь, t — время) производная единица скорости получается равной 1 м/с.
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ Глава 1.Элементы кинематики Рис.1.
Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы. Если материальная точка свободно движется в пространстве, то, как уже было сказано, она обладает тремя степенями свободы (координаты х, у и z), если она движется по некоторой поверхности, то двумя степенями свободы, если вдоль некоторой линии, то одной степенью свободы. Исключая t в уравнениях (1.1) и (1.2), получим уравнение траектории движения материальной точки. Траектория движения материальной точки — линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.
Рис. 2
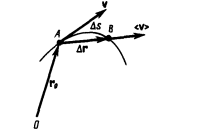
Рассмотрим движение материальной точки вдоль произвольной траектории (рис. 2). Отсчет времени начнем с момента, когда точка находилась в положении А. Длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути D s и является скалярной функцией времени: D s = D s(t). Вектор D r = r — r 0, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется перемещением. При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения |D r | равен пройденному пути D s.
Скорость Для характеристики движения материальной точки вводится векторная величина — скорость, которой определяется как быстрота движения, так и его направление в данный момент времени. Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор r0 (рис. 3). В течение малого промежутка времени D t точка пройдет путь D s и получит элементарное (бесконечно малое) перемещение D r.
Рис.3 Вектором средней скорости < v > называется отношение приращения D r радиуса-вектора точки к промежутку времени D t:
Направление вектора средней скорости совпадает с направлением D r. При неограниченном уменьшении D t средняя скорость стремится к предельному значению, которое называется мгновенной скоростью v:
Мгновенная скорость v, таким образом, есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости v направлен по касательной к траектории в сторону движения (рис. 3). По мере уменьшения D t путь D s все больше будет приближаться к |D r |, поэтому модуль мгновенной скорости
Таким образом, модуль мгновенной скорости равен первой производной пути по времени:
Если выражение (2.2) проинтегрировать по времени в пределах от от t 1 до t 2, то найдем длину пути, пройденного точкой промежуток времени от t 1 до t 2
Второй закон Ньютона Из опыта известно, что при одинаковых воздействиях различные тела неодинаково изменяют скорость своего движения, т.е., иными словами, приобретают различные ускорения. Ускорение зависит не только от величины воздействия, но и от свойств самого тела (от его массы). Масса тела — физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства. В настоящее время можно считать доказанным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10–12 их значения). Чтобы описывать воздействия, упоминаемые в первом законе Ньютона, вводят понятие силы. Под действием сил тела либо изменяют скорость движения, т. е. приобретают ускорения (динамическое проявление сил), либо деформируются, т. е. изменяют свою форму и размеры (статическое проявление сил). В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения. Итак, сила — это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры. Второй закон Ньютона — основной закон динамики поступательного движения — отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил. Если рассмотреть действие различных сил на одно и то же тело, то оказывается, что ускорение, приобретаемое телом, всегда прямо пропорционально равнодействующей приложенных сил: а ~ F ( т = const ). (6.1) При действии одной и той же силы на тела с разными массами их ускорения оказываются различными, а именно а ~ 1 / т (F = const). (6.2) Используя выражения (6.1) и (6.2) и учитывая, что сила и ускорение—величины векторные, можем записать а = k F/ m. (6.3) Соотношение (6.3) выражает второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела). В СИ коэффициент пропорциональности k= 1. Тогда
или
Учитывая, что масса материальной точки (тела) в классической механике есть величина постоянная, в выражении (6.4) ее можно внести под знак производной:
Векторная величина
численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения) этой материальной точки. Подставляя (6.6) в (6.5), получим
Это выражение — более общая формулировка второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе. Выражение (6.7) называется уравнением движения материальной точки. Единица силы в СИ — ньютон (Н): 1 Н — сила, которая массе 1 кг сообщает ускорение 1 м/с2 в направлении действия силы: 1 Н = 1 кг×м/с2. Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго. Действительно, в случае равенства нулю равнодействующей сил (при отсутствии воздействия на тело со стороны других тел) ускорение (см. (6.3)) также равно нулю. Однако первый закон Ньютона рассматривается как самостоятельный закон (а не как следствие второго закона), так как именно он утверждает существование инерциальных систем отсчета, в которых только и выполняется уравнение (6.7).
Рис. 10 В механике большое значение имеет принцип независимости действия сил: если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было. Согласно этому принципу, силы и ускорения можно разлагать на составляющие, использование которых приводит к существенному упрощению решения задач. Например, на рис. 10 действующая сила F = m a разложена на два компонента: тангенциальную силу F t, (направлена по касательной к траектории) и нормальную силу F n (направлена по нормали к центру кривизны). Используя выражения
Если на материальную точку действует одновременно несколько сил, то, согласно принципу независимости действия сил, под F во втором законе Ньютона понимают результирующую силу. Третий закон Ньютона Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки: F12 = – F21, (7.1) где F 12 — сила, действующая на первую материальную точку со стороны второй; F 21 — сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы. Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.
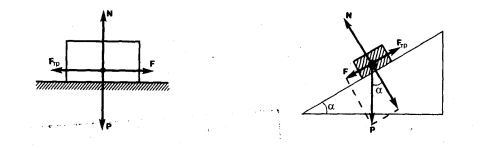
Силы трения Обсуждая до сих пор силы, мы не интересовались их происхождением. Однако в механике мы будем рассматривать различные силы: трения, упругости, тяготения. Из опыта известно, что всякое тело, движущееся по горизонтальной поверхности другого тела, при отсутствии действия на него других сил с течением времени замедляет свое движение и в конце концов останавливается. Это можно объяснить существованием силы трения, которая препятствует скольжению соприкасающихся тел друг относительно друга. Силы трения зависят от относительных скоростей тел. Силы трения могут быть разной природы, но в результате их действия механическая энергия всегда превращается во внутреннюю энергию соприкасающихся тел. Различают внешнее (сухое) и внутреннее (жидкое или вязкое) трение. Внешним трением называется трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении. Если соприкасающиеся тела неподвижны друг относительно друга, говорят о трении покоя, если же происходит относительное перемещение этих тел, то в зависимости от характера их относительного движения говорят о трении скольжения, качения или верчения. Обсудим некоторые закономерности внешнего трения. Это трение обусловлено шероховатостью соприкасающихся поверхностей; в случае же очень гладких поверхностей трение обусловлено силами межмолекулярного притяжения. Рассмотрим лежащее на плоскости тело (рис. 11), к которому приложена горизонтальная сила F. Тело придет в движение лишь тогда, когда приложенная сила F будет больше силы трения Fтр. Французские физики Г. Амонтон (1663—1705) и Ш. Кулон (1736—1806) опытным путем установили следующий закон: сила трения скольжения F тр пропорциональна силе N нормального давления, с которой одно тело действует на другое: F тр = f N, (8.1) где f — коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей.
Рис. 11 Рис. 12 Найдем значение коэффициента трения. Если тело находится на наклонной плоскости с углом наклона a (рис.12), то оно приходит в движение, только когда тангенциальная составляющая F силы тяжести Р больше силы трения Fтр. Следовательно, в предельном случае (начало скольжения тела) F = F тр. или P sin a0 = f N = f P cos a0,откуда f = tga0. Таким образом, коэффициент трения равен тангенсу угла a0, при котором начинается скольжение тела по наклонной плоскости.
§ 9. Закон сохранения импульса. Центр масс Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются — внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной). Если мы имеем механическую систему, состоящую из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направлены, т. е. геометрическая сумма внутренних сил равна нулю. Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны m 1, m 2,.... mn, и v 1, v 2,..., v n. Пусть
Складывая почленно эти уравнения, получаем
Но так как геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю, то
или
где В случае отсутствия внешних сил (рассматриваем замкнутую систему)
Последнее выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени. Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выполняется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т. е. закон сохранения импульса — фундаментальный закон природы. Отметим, что, согласно (9.1), импульс сохраняется и для незамкнутой системы, если геометрическая сумма всех внешних сил равна нулю. В механике Галилея—Ньютона из-за независимости массы от скорости импульс системы может быть выражен через скорость ее центра масс. Центром масс (или центром инерции) системы материальных точек называется воображаемая точка С,положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен
где mi и r i — соответственно масса и радиус-вектор i -й материальной точки; n — число материальных точек в системе;
Учитывая, что p i = mi v i, a
т. е. импульс системы равен произведению массы системы на скорость ее центра масс. Подставив выражение (9.2) в уравнение (9.1), получим
т. е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе. Выражение (9.6) представляет собой закон движения центра масс. В соответствии с (9.2) из закона сохранения импульса вытекает, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.
Глава 3. Работа и энергия Энергия, работа, мощность Энергия — универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других — переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той иди иной форме) одним телом другому телу, равна энергии, полученной последним телом. Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 1282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.13.201 (0.155 с.) |

 (2.1)
(2.1)

 (2.2)
(2.2) (2.3)
(2.3)
 (6.4)
(6.4) (6.5)
(6.5) (6.6)
(6.6)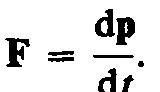 (6.7)
(6.7)
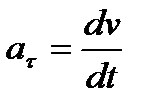 и
и  , а также
, а также  , можно записать:
, можно записать:
 — равнодействующие внутренних сил, действующих на каждое из этих тел, a
— равнодействующие внутренних сил, действующих на каждое из этих тел, a  — равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы:
— равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы:
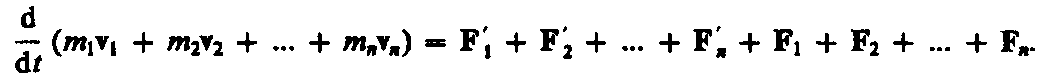

 (9.1)
(9.1) — импульс системы. Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему.
— импульс системы. Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему. (9.2)
(9.2) (9.3)
(9.3) – масса системы. Скорость центра масс
– масса системы. Скорость центра масс (9.4)
(9.4) есть импульс р системы, можно написать
есть импульс р системы, можно написать (9.5)
(9.5) (9.6)
(9.6)


