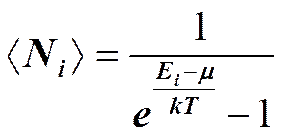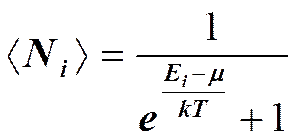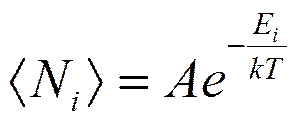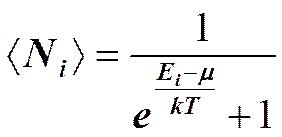Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы атомной физики и квантовой механики.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Элементы атомной физики и квантовой механики.
Корпускулярно-волновой дуализм свойств вещества.
(квадрат модуля Y-функции) имеет смысл плотности вероятности, т. е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами х, у, z. Таким образом, физический смысл имеет не сама Y-функция, а квадрат ее модуля |Y|2, которым задается интенсивность волн де Бройля.
Уравнение Шредингера.
где
Движение свободной частицы. U=0
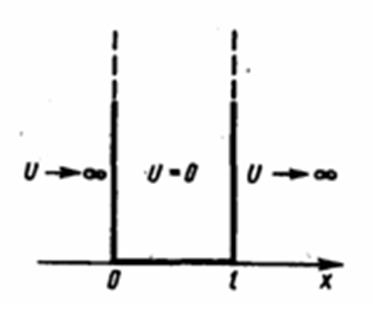
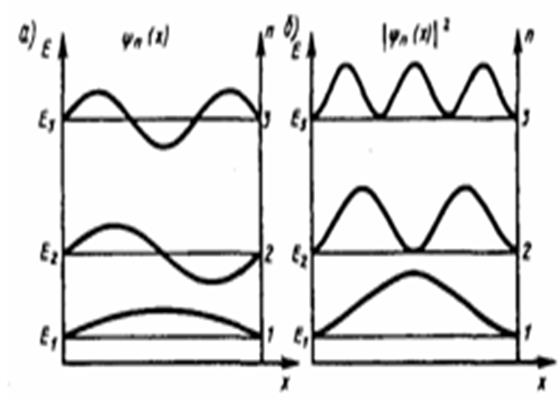
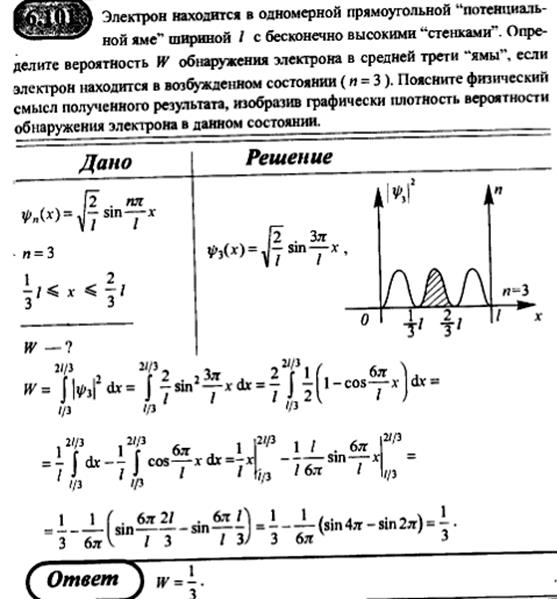
Частица в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками».
т.к. y (0)=0, то В =0.
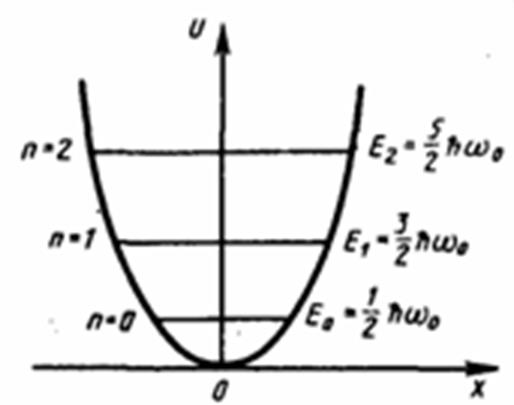
В теории дифференциальных уравнений доказывается, что уравнение решается только при собственных значениях энергии
E 0=1/2ћw0 . — энергия нулевых колебаний.
Водородоподобных систем.
Полная система квантовых чисел. Принцип Паули. К-, L-, М- оболочки атома. Рентгеновский спектр. Закон Мозли. Энергетический спектр атомов и молекул. Заполнение электронных оболочек и периодическая система элементов.
Решение задачи об энергетических уровнях электрона для атома водорода сводится к задаче о движении электрона в кулоновском поле ядра. Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом 2е (для атома водорода Z=1),
где r — расстояние между электроном и ядром. Состояние электрона в атоме водорода описывается волновой функцией y, удовлетворяющей стационарному уравнению Шредингера:
где т — масса электрона, Е — полная энергия электрона в атоме.
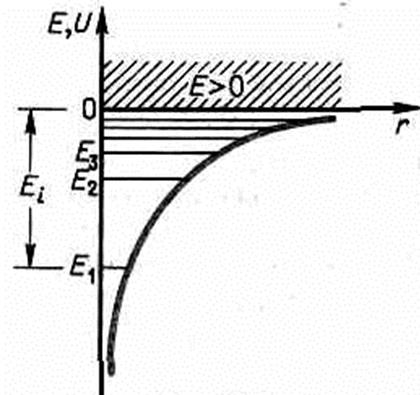
1. Энергия. Из уравнения Шредингера Решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней E 1, E 2, E 3 и т д. Самый нижний уровень Е1— основной, все остальные (En>E1 n=2, 3,...) — возбужденные.
Ei=-E1= те4/ (8h2e20) =13,55 эВ. 1. Квантовые числа. В квантовой механике доказывается, что уравнению Шредингера (223.2) удовлетворяют собственные функции yn m l(r, q, j), определяемые тремя квантовыми числами: главным n , орбитальным l. магнитным ml .
n=1,2,3,....
l= 0, 1,..., (n-1), т. е. всего n значений, и определяет момент импульса электрона в атоме. Из решения уравнений Шредингера следует также, что вектор Le момента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция
где ml — магнитное квантовое число, которое при заданном l может принимать значения ml=0, ±1, ±2,..., ±l, т. е. всего 2 l +1 значений.
Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число ml характеризует ориентацию электронного облака в пространстве. В атомной физике, по аналогии со спектроскопией, состояние электрона, характеризующееся квантовыми числами l =0, называют s-состоянием (электрон в этом состоянии называют s-электроном), l =1 — р-состоянием, l =2 — d-состоянием,
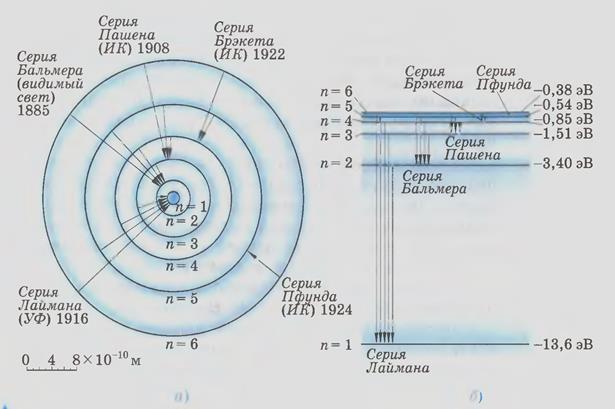
В квантовой механике вводятся правила отбора, ограничивающие число возможных переходов электронов в атоме, связанных с испусканием и поглощением света. Теоретически доказано и экспериментально подтверждено, что для дипольного излучения электрона, движущегося в центрально-симметричном поле ядра, могут осуществляться только такие переходы, для которых: 1) изменение орбитального квантового числа Dl удовлетворяет условию Dl=±1; 2) изменение магнитного квантового числа Dml удовлетворяет условию Dml=0, ±1. Учитывая число возможных состояний, соответствующих данному n, и правило отбора, рассмотрим спектральные линии атома водорода (рис. 304):
np®1s (n=2,3,...); Серии Бальмера. np®2s, ns®-2p, nd®2p (n=3, 4,...) И т. д.
Квантовая статистика.
Для систем частиц, образованных фермионами — частицами с полуцелым спином, числа заполнения могут принимать лишь два значения: 0 для свободных состояний и 1 для занятых. Сумма всех чисел заполнения должна быть равна числу частиц системы. Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии, т. е. определить средние числа заполнения <Ni>. Идеальный газ из бозонов — бозе-газ — описывается квантовой статистикой Бозе — Эйнштейна.
Это распределение называется распределением Бозе — Эйнштейна. Здесь < Ni > — среднее число бозонов в квантовом состоянии с энергией Ei, k — постоянная Больцмана, Т — термодинамическая температура, m — химический потенциал; m не зависит от энергии, а определяется только температурой и плотностью числа частиц. Химический потенциал определяет изменение внутренней энергии системы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внутренняя энергия (энтропия, объем), фиксированы. Идеальный газ из фермионов — ферми-газ — описывается квантовой статистикой Ферми — Дирака. Распределение фермионов по энергиям имеет вид
где <Ni>—среднее число фермионов в квантовом состоянии с энергией Ei, m — химический потенциал. Если е(Ei-m)/(kT)>>1, то распределения Бозе — Эйнштейна и Ферми — Дирака переходят в классическое распределение Максвелла — Больцмана:
где
Таким образом, при высоких температурах оба «квантовых» газа ведут себя подобно классическому газу. Температурой вырождения То называется температура, ниже которой отчетливо проявляются квантовые свойства идеального газа, обусловленные тождественностью частиц, т. е. Т 0 — температура, при которой вырождение становится существенным. Если T >> T 0, то поведение системы частиц (газа) описывается классическими законами. Вырожденный электронный газ в металлах Распределение электронов по различным квантовым состояниям подчиняется принципу Паули, согласно которому в одном состоянии не может быть двух одинаковых (с одинаковым набором четырех квантовых чисел) электронов, они должны отличаться какой-то характеристикой, например направлением спина. Следовательно, по квантовой теории, электроны в металле не могут располагаться на самом низшем энергетическом уровне даже при 0 К. Принцип Паули вынуждает электроны взбираться вверх «по энергетической лестнице». Электроны проводимости в металле можно рассматривать как идеальный газ, подчиняющийся распределению Ферми — Дирака. Если m0 — химический потенциал электронного газа при Т= 0К, то, среднее число < N(E)> электронов в квантовом состоянии с энергией E равно
Для фермионов (электроны являются фермионами) среднее число частиц в квантовом состоянии и вероятность заселенности квантового состояния совпадают, так как квантовое состояние либо может быть не заселено, либо в нем будет находиться одна частица. Это означает, что для фермионов < N (E)> = f (E), где f (E) — функция распределения электронов по состояниям. Из (236.1) следует, что при Т= 0К
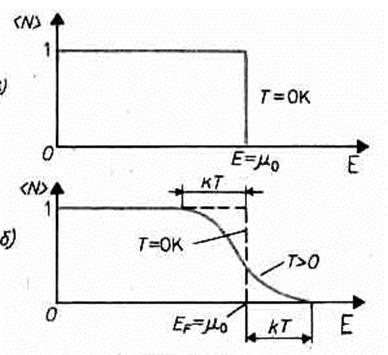
функция распределения < N (E)³1, если E <m0, и < N (E)³0, если E >m0. В области энергий от 0 до m0 функция < N (E)> равна единице. При E=m0 она скачкообразно изменяется до нуля. Это означает, что при Т=0 К все нижние квантовые состояния, вплоть до состояния с энергией E=m0, заполнены электронами, а все состояния с энергией, большей m0, свободны. Следовательно, m0есть не что иное, как максимальная кинетическая энергия, которую могут иметь электроны проводимости в металле при 0 К. Эта максимальная кинетическая энергия называется энергией Ферми и обозначается ЕF (EF=m0). Поэтому распределение Ферми — Дирака обычно записывается в виде
Наивысший энергетический уровень, занятый электронами, называется уровнем Ферми. Уровню Ферми соответствует энергия Ферми ЕF, которую имеют электроны на этом уровне. Уровень Ферми, очевидно, будет тем выше, чем больше плотность электронного газа. Работу выхода электрона из металла нужно отсчитывать не от дна «потенциальной ямы», как это делалось в классической теории, а от уровня Ферми, т. е. от верхнего из занятых электронами энергетических уровней. При температурах, отличных от 0 К, функция распределения Ферми — Дирака плавно изменяется от 1 до 0 в узкой области (порядка kT) в окрестности ЕF (рис. 312, б). В тепловом движении участвует лишь небольшое число электронов, например при комнатной температуре Т» 300 К и температуре вырождения T0=3•104 К,— это 10-5 от общего числа электронов. Если (Е-EF)>>kT тогда распределение Ферми — Дирака переходит в распределение Максвелла — Больцмана. Таким образом, при (E-EF}>>kT, т. е. при больших значениях энергии, к электронам в металле применима классическая статистика, в то же время, когда (E-EF)<<kT, к ним применима только квантовая статистика Ферми — Дирака. Сверхпроводимость.
Как показал немецкий физик В. Мейсснер, в сверхпроводящем состоянии магнитное поле в толще сверхпроводника отсутствует. Это означает, что при охлаждении сверхпроводника ниже критической температуры магнитное поле из него вытесняется (эффект Мейсснера). Физическая природа сверхпроводимости была понята в 1957 г. на основе теории (создана Ландау в 1941 г.) сверхтекучести гелия. Теория сверх- проводимости создана американскими физиками Д. Бардином (р. 1908), Л. Купером (р. 1930) и Д. Шриффером (р. 1931) и усовершенствована Н. Н. Боголюбовым. Качественно явление сверхпроводимости можно объяснить так. Между электронами металла помимо кулоновского отталкивания, в достаточной степени ослабляемого экранирующим действием положительных ионов решетки, в результате электрон-фононного взаимодействия (взаимодействия электронов с колебаниями решетки) возникает слабое взаимное притяжение. Это взаимное притяжение при определенных условиях может преобладать над отталкиванием. В результате электроны проводимости, притягиваясь, образуют своеобразное связанное состояние, называемое куперовской парой. «Размеры» пары много больше (примерно на четыре порядка) среднего межатомного расстояния, т. е. между электронами, «связанными» в пару, находится много «обычных» электронов. Чтобы куперовскую пару разрушить (оторвать один из ее электронов), надо затратить некоторую энергию, которая пойдет на преодоление сил притяжения электронов пары. Такая энергия может быть в принципе получена в результате взаимодействия с фононами. Однако пары сопротивляются своему разрушению. Это объясняется тем, что существует не одна пара, а целый ансамбль взаимодействующих друг с другом куперовских пар. Электроны, входящие в куперовскую пару, имеют противоположно направленные спины. Поэтому спин такой пары равен нулю и она представляет собой бозон. К бозонам принцип Паули неприменим, и число бозе-частиц, находящихся в одном состоянии, не ограничено. Поэтому при сверхнизких температурах бозоны скапливаются в основном состоянии, из которого их довольно трудно перевести в возбужденное. Система бозе-частиц — куперовских пар, обладая устойчивостью относительно возможности отрыва электрона, может под действием внешнего электрического поля двигаться без сопротивления со стороны проводника, что и приводит к сверхпроводимости. Зонная теория твердых тел.
Энергетические зоны в кристаллах. Распределение электронов по энергетическим зонам. Металлы, полупроводники и диэлектрики. Контакт двух разнородных металлов. Явления Пельтье и Зеебека. Собственная и примесная проводимость полупроводников. p-n переход и его вольтамперная характеристика. Элементы атомной физики и квантовой механики.
Корпускулярно-волновой дуализм свойств вещества.
(квадрат модуля Y-функции) имеет смысл плотности вероятности, т. е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами х, у, z. Таким образом, физический смысл имеет не сама Y-функция, а квадрат ее модуля |Y|2, которым задается интенсивность волн де Бройля.
Уравнение Шредингера.
где
Движение свободной частицы. U=0
Частица в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками».
т.к. y (0)=0, то В =0.
В теории дифференциальных уравнений доказывается, что уравнение решается только при собственных значениях энергии
E 0=1/2ћw0 . — энергия нулевых колебаний.
Водородоподобных систем.
Полная система квантовых чисел. Принцип Паули. К-, L-, М- оболочки атома. Рентгеновский спектр. Закон Мозли. Энергетический спектр атомов и молекул. Заполнение электронных оболочек и периодическая система элементов.
Решение задачи об энергетических уровнях электрона для атома водорода сводится к задаче о движении электрона в кулоновском поле ядра. Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом 2е (для атома водорода Z=1),
где r — расстояние между электроном и ядром. Состояние электрона в атоме водорода описывается волновой функцией y, удовлетворяющей стационарному уравнению Шредингера:
где т — масса электрона, Е — полная энергия электрона в атоме.
1. Энергия. Из уравнения Шредингера Решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней E 1, E 2, E 3 и т д. Самый нижний уровень Е1— основной, все остальные (En>E1 n=2, 3,...) — возбужденные.
Ei=-E1= те4/ (8h2e20) =13,55 эВ. 1. Квантовые числа. В квантовой механике доказывается, что уравнению Шредингера (223.2) удовлетворяют собственные функции yn m l(r, q, j), определяемые тремя квантовыми числами: главным n , орбитальным l. магнитным ml .
n=1,2,3,....
l= 0, 1,..., (n-1), т. е. всего n значений, и определяет момент импульса электрона в атоме. Из решения уравнений Шредингера следует также, что вектор Le момента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция
где ml — магнитное квантовое число, которое при заданном l может принимать значения ml=0, ±1, ±2,..., ±l, т. е. всего 2 l +1 значений.
Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число ml характеризует ориентацию электронного облака в пространстве. В атомной физике, по аналогии со спектроскопией, состояние электрона, характеризующееся квантовыми числами l =0, называют s-состоянием (электрон в этом состоянии называют s-электроном), l =1 — р-состоянием, l =2 — d-состоянием,
В квантовой механике вводятся правила отбора, ограничивающие число возможных переходов электронов в атоме, связанных с испусканием и поглощением света. Теоретически доказано и экспериментально подтверждено, что для дипольного излучения электрона, движущегося в центрально-симметричном поле ядра, могут осуществляться только такие переходы, для которых: 1) изменение орбитального квантового числа Dl удовлетворяет условию Dl=±1; 2) изменение магнитного квантового числа Dml удовлетворяет условию Dml=0, ±1. Учитывая число возможных состояний, соответствующих данному n, и правило отбора, рассмотрим спектральные линии атома водорода (рис. 304):
np®1s (n=2,3,...); Серии Бальмера. np®2s, ns®-2p, nd®2p (n=3, 4,...) И т. д.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 770; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.016 с.) |

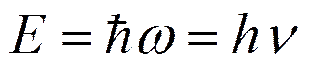




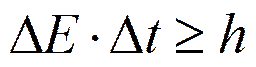
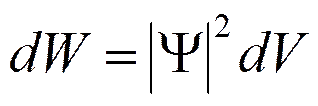
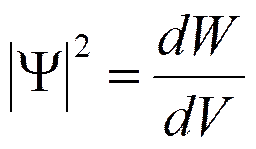
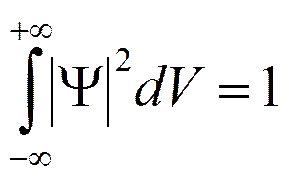
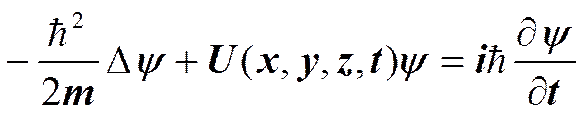
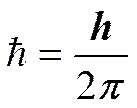 , т— масса частицы, D—оператор Лапласа
, т— масса частицы, D—оператор Лапласа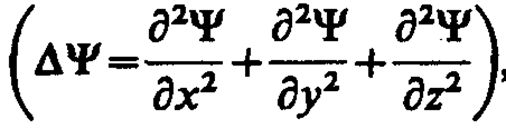
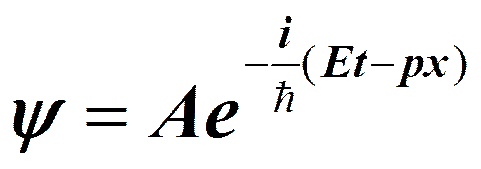
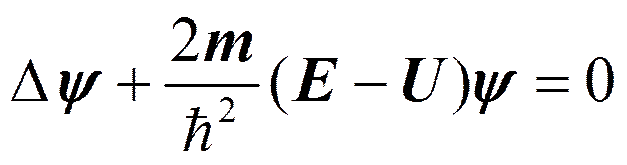

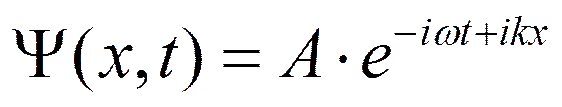
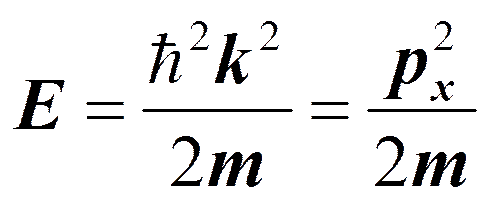

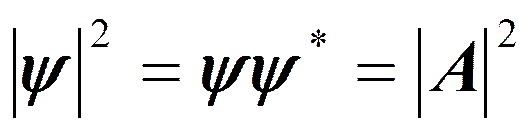
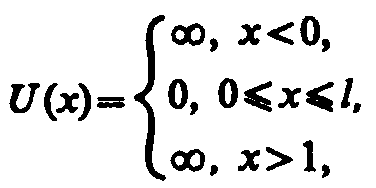
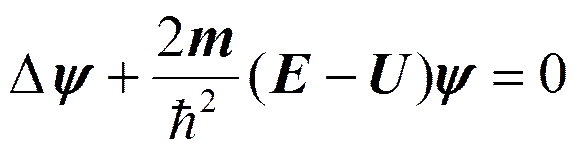
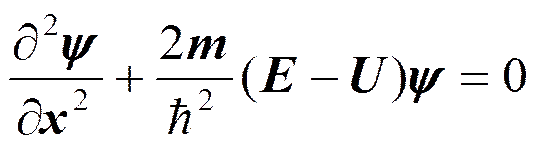

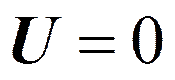
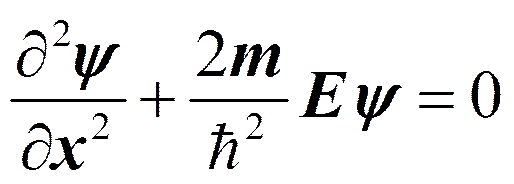
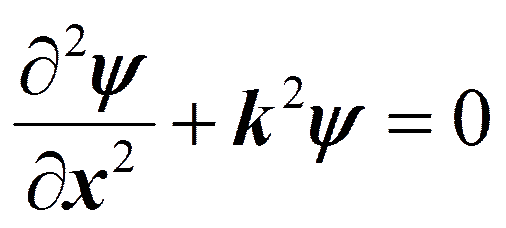
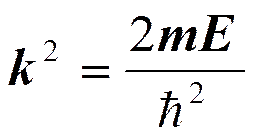
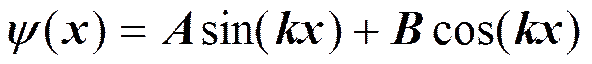

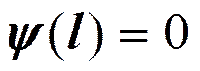

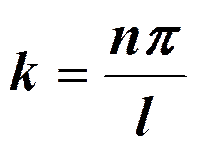
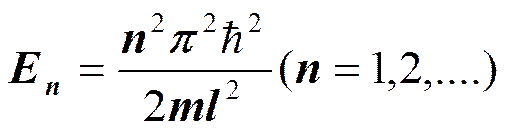
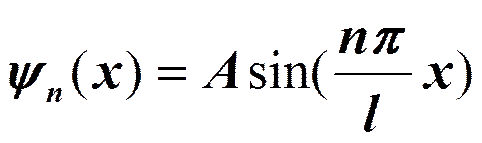
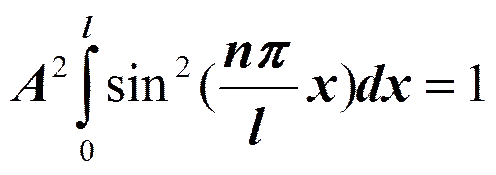
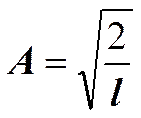
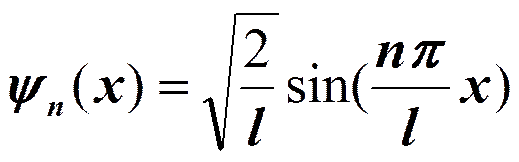

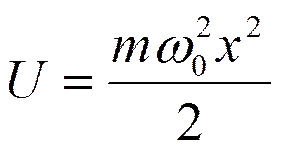

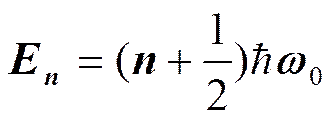

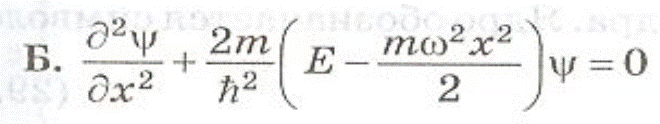
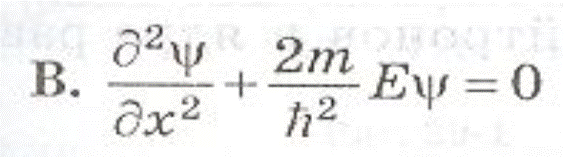
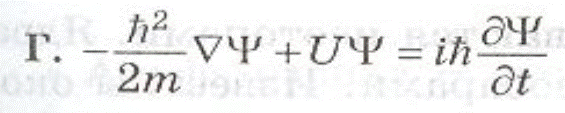
 Квантовая механика
Квантовая механика ,
,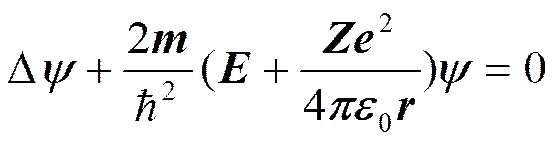
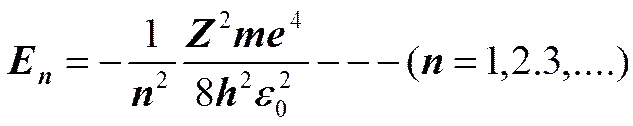
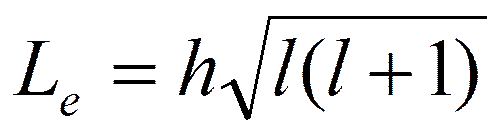
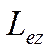 на направление z внешнего магнитного поля принимает квантованные значения, кратные h
на направление z внешнего магнитного поля принимает квантованные значения, кратные h