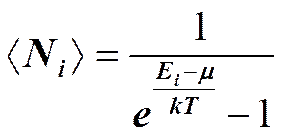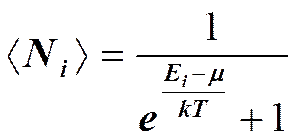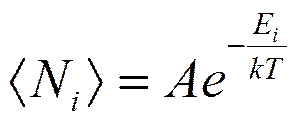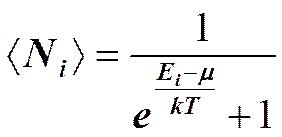Сплошной рентгеновский спектр называют тормозным спектром.

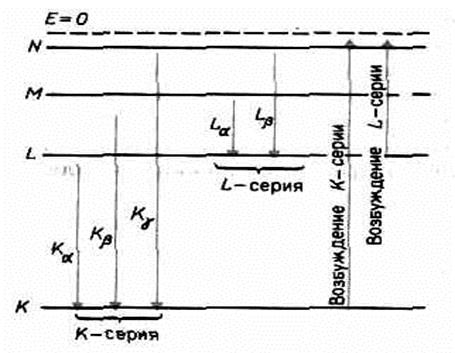
При достаточно большой энергии бом­бардирующих анод электронов на фоне сплошного спектра появляются отдель­ные резкие линии — линейчатый спектр, определяемый материалом анода и назы­ваемый потому характеристическим рент­геновским спектром.

По сравнению с оптическими спектра­ми характеристические рентгеновские спектры элементов совершенно однотипны и состоят из нескольких серий, обозначае­мых К, L, М, N и О. Каждая серия, в свою очередь, содержит небольшой набор от­дельных линий, обозначаемых в порядке убывания длины волны индексами a, b, g,... (K_a, К_b, K_g,..., l_a, l_b, l_g,...).

Исследуя рентгеновские спектры эле­ментов, Г. Мозли (1887—1915) установил в 1913г. соотно­шение, называемое законом Мозли:

,
где n — частота, соответствующая данной линии характеристического рентгеновско­го излучения, R — постоянная Ридберга, s—постоянная экранирования, m=1, 2, 3,... (определяет рентгеновскую серию), n принимает целочисленные значения с m+1 (определяет отдельную линию со­ответствующей серии).

Смысл постоянной экранирования за­ключается в том, что на электрон, совер­шающий переход, соответствующий неко­торой линии, действует не весь заряд ядра Ze, а заряд (Z-s )е, ослабленный экрани­рующим действием других электронов. Например, для K_a-линии s=1, и закон Мозли запишется в виде

Молекулы, химические связи. понятие об энергетических уровнях

Молекула — наименьшая частица вещест­ва, состоящая из одинаковых или различ­ных атомов, соединенных между собой химическими связями, и являющаяся но­сителем его основных химических и физи­ческих свойств. Химические связи обус­ловлены взаимодействием внешних, вален­тных электронов атомов.

Ионная связь (например, в молекулах NaCl, KBr) осуществляется электростати­ческим взаимодействием атомов при пере­ходе электрона одного атома к другому, т. е. при образовании положительного и отрицательного ионов.
Ковалентная связь (например, в молекулах Н₂, С₂, СО) осуществляется при обобществлении ва­лентных электронов двумя соседними атомами (спины валентных электронов до­лжны быть антипараллельны). Ковалент­ная связь объясняется на основе принципа неразличимости тождественных частиц, например электронов в моле­куле водорода. Неразличимость частиц приводит к специфическому взаимодейст­вию между ними, называемому обменным взаимодействием. Это чисто квантовый эффект, не имеющий классического объяс­нения, но его можно себе представить так, что электрон каждого из атомов молекулы водорода проводит некоторое время у яд­ра другого атома и, следовательно, осуще­ствляется связь обоих атомов, образую­щих молекулу. При сближении двух водо­родных атомов до расстояний порядка боровского радиуса возникает их взаим­ное притяжение и образуется устойчивая молекула водорода.

Молекула является квантовой систе­мой; она описывается уравнением Шре­дингера.

Квантовая статистика.

Распределения Бозе-Эйнштейна и Ферми-Дирака. Вырожденный электронный газ в металлах. Энергия Ферми. Влияние температуры на распределение электронов. Сверхпроводимость. Квантовая теория теплоемкости твердых тел.

Квантовая статистика Бозе — Эйнштейна и Ферми — Дирака

Состояние системы невзаимодействующих частиц за­дается с помощью так называемых чисел заполнения N_i — чисел, указывающих сте­пень заполнения квантового состояния (характеризуется данным набором i кван­товых чисел) частицами системы, состоя­щей из многих тождественных частиц. Для систем частиц, образованных бозона­ми — частицами с нулевым или целым спином, числа заполнения мо­гут принимать любые целые значения: О, 1, 2,....

Для систем частиц, обра­зованных фермионами — частицами с по­луцелым спином, числа запол­нения могут принимать лишь два значе­ния: 0 для свободных состояний и 1 для занятых. Сумма всех чисел за­полнения должна быть равна числу частиц системы. Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии, т. е. определить средние числа заполнения <N_i>.

Идеальный газ из бозонов — бозе-газ — описывается квантовой статистикой Бозе — Эйнштейна.

Это распределение называется распреде­лением Бозе — Эйнштейна.

Здесь < Ni > — среднее число бозонов в квантовом со­стоянии с энергией E_i, k — постоянная Больцмана, Т — термодинамическая тем­пература, m — химический потенциал; m не зависит от энергии, а определяется только температурой и плотностью числа частиц. Химический потенциал определяет изменение внутренней энергии системы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внутренняя энергия (энтропия, объем), фиксированы.

Идеальный газ из фермионов — ферми-газ — описывается квантовой стати­стикой Ферми — Дирака. Распределение фермионов по энергиям имеет вид

где <N_i>—среднее число фермионов в квантовом состоянии с энергией E_i, m — химический потенциал.

Если е(^Ei-m)/(kT)>>1, то распределения Бозе — Эйнштейна и Ферми — Дирака переходят в классическое распределение Максвелла — Больцмана:

 

где

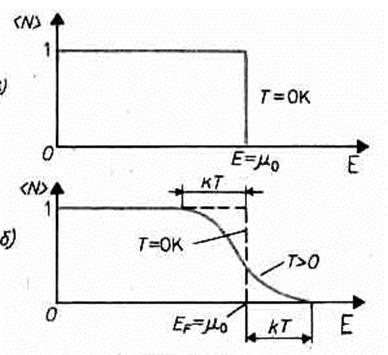
Таким образом, при высоких температурах оба «квантовых» газа ведут себя подобно классическому газу.

Температурой вырождения То называ­ется температура, ниже которой отчетливо проявляются квантовые свойства идеаль­ного газа, обусловленные тождественно­стью частиц, т. е. Т ₀ — температура, при которой вырождение становится су­щественным. Если T >> T ₀, то поведение системы частиц (газа) описывается клас­сическими законами.

Вырожденный электронный газ в металлах

Распределение электронов по различным квантовым состояниям подчиняется прин­ципу Паули, согласно которо­му в одном состоянии не может быть двух одинаковых (с одинаковым набором четы­рех квантовых чисел) электронов, они до­лжны отличаться какой-то характеристи­кой, например направлением спина. Сле­довательно, по квантовой теории, электро­ны в металле не могут располагаться на самом низшем энергетическом уровне да­же при 0 К. Принцип Паули вынуждает электроны взбираться вверх «по энергети­ческой лестнице».

Электроны проводимости в металле можно рассматривать как идеальный газ, подчиняющийся распределению Ферми — Дирака. Если m₀ — химический по­тенциал электронного газа при Т= 0К, то, среднее число < N(E)> электронов в квантовом состоянии с энер­гией E равно

Для фермионов (электроны являются фермионами) среднее число частиц в кванто­вом состоянии и вероятность заселенности квантового состояния совпадают, так как квантовое состояние либо может быть не заселено, либо в нем будет находиться одна частица. Это означает, что для фермионов < N (E)> = f (E), где f (E) — функция распределения электронов по состояниям. Из (236.1) следует, что при Т= 0К

 

функция распределения < N (E)³1, если E <m₀, и < N (E)³0, если E >m₀. В области энергий от 0 до m₀ функция < N (E)> равна единице. При E=m₀ она скачкообразно изменяется до нуля. Это означает, что при Т=0 К все нижние квантовые состояния, вплоть до состояния с энергией E=m₀, заполнены электронами, а все состояния с энергией, большей m₀, свободны. Следовательно, m₀есть не что иное, как максимальная кинетическая энергия, которую могут иметь электроны проводимости в металле при 0 К. Эта мак­симальная кинетическая энергия называ­ется энергией Ферми и обозначается Е_F (E_F=m₀). Поэтому распределение Ферми — Дирака обычно записывается в виде

Наивысший энергетический уровень, занятый электронами, называется уровнем Ферми. Уровню Ферми соответствует энер­гия Ферми Е_F, которую имеют электроны на этом уровне. Уровень Ферми, очевидно, будет тем выше, чем больше плотность электронного газа. Работу выхода элек­трона из металла нужно отсчитывать не от дна «потенциальной ямы», как это дела­лось в классической теории, а от уровня Ферми, т. е. от верхнего из занятых элек­тронами энергетических уровней.

При температурах, отличных от 0 К, функция распределения Ферми — Дирака плавно изменяется от 1 до 0 в узкой области (порядка kT) в окрестности Е_F (рис. 312, б). В тепловом движении участвует лишь небольшое число электронов, напри­мер при комнатной температуре Т» 300 К и температуре вырождения T₀=3•10⁴ К,— это 10^-5 от общего числа электронов.

Если (Е-E_F)>>kT тогда распределение Ферми — Дирака переходит в распределе­ние Максвелла — Больцмана. Таким об­разом, при (E-E_F}>>kT, т. е. при больших значениях энергии, к электронам в металле применима классическая статистика, в то же время, когда (E-E_F)<<kT, к ним при­менима только квантовая статистика Фер­ми — Дирака.