
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механика и молекулярная физика.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Механика и молекулярная физика. ЧАСТЬ 1. МЕХАНИКА. Введение. «Физика» - от греческого “physis” - т.е. природа. Физика дает описание всех явлений в природе. Поэтому физика является основой естествознания (включая астрономию, отдельные разделы химии, акустики и других проявлений реального мира). Одновременно физика является основой техники и современных технологий. В СТАНКИНе читается курс «ФОПИ» - Физические основы получения информации. В этом семестре мы будем изучать механику и некоторые вопросы термодинамики и статистической физики. Механика = кинематика + динамика. Механика: классическая (или Ньютоновская), релятивистская, статистическая, квантовая. Физика – математически точная наука. Главное свойство этого раздела – воспроизводимость результатов. В физике есть два направления теоретическая и экспериментальная физика. Они взаимно дополняют друг друга. Иногда основное, передовое значение имеет теория, в других случаях – эксперимент. Это означает, что иногда первый шаг делает теория, а эксперимент проверяет и подтверждает результаты теоретических предсказаний. В других случаях полученные экспериментальные результаты объясняются, интерпретируются теоретиками. Именно в физике зародились многие математические понятия и методы. Математика – язык физики. Практически всегда новый раздел математики находит применения для описания физических явлений. Физика не есть «совершенное, но застывшее здание». Это, скорее, развивающаяся, растущая система. Появляются новые данные, новые теории и «здание физики» изменяется. Но всегда «старая» физика входит составной частью в в «новую физику». Мы обсудим этот вопрос детальнее при изучении элементов релятивистской механики.
§2. Механическое движение и его основные понятия. Механическое движение – это изменение положения тела в пространстве с течением времени. Для математического описания такого движения надо ввести понятие системы отсчета. Так как экспериментально было установлено, что геометрическое пространство трехмерно, то для введения системы отсчета надо указать четыре точки, не лежащие на одной прямой или в одной плоскости (например, четыре звезды). Одну из них принимают за начало отсчета, остальные указывают направление трех координатных осей. Если оси ортогональны (перпендикулярны), то система отсчета называется Декартовой. Если же углы между осями отличаются от прямых, то систему называют косоугольной. Положительные направления осей указываются ортами или единичными векторами (это безразмерные векторы, длина – модуль – которых равен единице). В Декартовых системах координат обычно используют три орта Иногда (это связано с симметрией физической системы) удобнее использовать сферические или цилиндрические системы координат. Между понятиями «система отсчета» и «система координат» есть некоторое различие. Оно состоит в том, что для введения системы отсчета кроме направления осей и начала отсчета необходимо указать масштаб. Так, линейные размеры принято указывать в метрах. Это не всегда удобно. Например, в атомной физике используется единица, которая называется Ангстрем (1А= 10-10 м). В настоящее время принято использовать Международную систему единиц (СИ). В этой системе основными механическими единицами считаются метр (м), килограмм (кг), секунда (с). С их помощью вводят «производные» величины. Например, работа или энергия измеряются в Джоулях, 1 Дж имеет размерность м кг/с. Есть много и других физических величин, с которыми мы будем знакомиться постепенно.
§3. Основные понятия классической механики. Выделяют классическую механику материальной точки, системы материальных точек, абсолютно твердого тела и классической жидкости. Сначала мы изучим механику материальной точки. Материальной точкой называется объект малых размеров, форма которого не влияет на характер движения. Например, дробинка, брошенная в аудитории – материальная точка, а плоский клочок бумаги тех же размеров – нет. Важным требованием является «малость» скорости движения объекта. «Малость» в данном случае означает, что скорость движения много меньше скорости света. Переход к скоростям, сравнимым со скоростью света требует замены классической механики на релятивистскую механику. Кроме радиус-вектора в классической механике используют понятия скорости и ускорения. Рассмотрим эти понятия детально. Пусть материальная точка движется вдоль оси х. Если установлено, что в момент времени t1 точка имела координату х(t1), а в момент – координату х(t2), то средней скоростью за время
Следует помнить, что скорость имеет определенное направление, то есть является векторной величиной. Поэтому в рассмотренном случае правильнее писать
Средняя скорость – грубая характеристика движения. Она становится точнее, если уменьшать
где подразумевается, что орт не зависит от времени. Если же движение происходит в трехмерном пространстве, то для получения мгновенной скорости надо продифференцировать радиус-вектор:
Аналогичным образом вводят среднее и мгновенное ускорения. Ускорение – это скорость изменения скорости, то есть мгновенное ускорение определяется первой производной (по времени) скорости, или, что то же самое, второй производной радиус-вектора:
Необходимо помнить, что скаляр (модуль скорости, ускорения) это одно число, тогда как вектор (те же величины) это три числа, три проекции. Поэтому вектор надо обязательно отмечать стрелкой над обозначением величины. Разумеется, это относится ко всем векторным величинам. Нарушение этого правила – грубая ошибка. В любом равенстве обе части, левая и правая, всегда должны иметь одинаковый смысл – быть либо векторными, либо скалярными. Кстати, векторное уравнение, – это всегда три скалярных уравнения. Приведем один пример определения мгновенного ускорения по заданному радиус-вектору. Пусть
Согласно определению мгновенной скорости для её нахождения радиус-вектор надо продифференцировать по времени. Проводя это дифференцирование, найдем Для получения мгновенного ускорения следует продифференцировать мгновенную скорость. Дифференцируя, получим:
Другими важными понятиями в классической механике являются импульс и кинетическая энергия. Импульсом материальной точки называют векторную величину, полученную при перемножении массы точки на её мгновенную скорость:
Легко заметить, что размерность импульса равна кг м/с. Специального названия эта единица не имеет. Энергия в физике – это величина, характеризующая способность механической системы совершать работу. Выделяют кинетическую энергию, зависящую от массы и скорости, и потенциальную энергию, зависящую от положения системы в пространстве. По определению, кинетическая энергия материальной точки равна
Эта формула пригодна для классической механики. При больших скоростях масса начинает зависеть от скорости и в релятивистском приближении формула требует обобщения. Потенциальную энергию можно в общем виде записать так:
Сумма двух этих энергий называется полной энергией системы,
Как было сказано, энергия измеряется в Джоулях, Дж. Импульс и полная энергия системы это выделенные в физике величины. В отличие от других комбинаций величин Для динамики особенно важно понятие силы. Все мы интуитивно знаем, что физическая сила существует. Мы можем экспериментально наблюдать действие силы. Например, если мы будем толкать камешек прутиком, то прутик согнется, а камешек начнет двигаться. Это – проявление силы. Если прутик сгибается больше, то мы говорим, что действующая сила тоже больше. Уже из этого описания опыта ясно, что сила – векторная величина. Её обычно обозначают как В классической механике силу связывают с изменением импульса:
Если имеется материальная точка, то на неё может действовать несколько сил одновременно. Тогда говорят, что к точке приложена равнодействующая всех сил. Равнодействующую находят путем векторного сложения всех действующих сил. Если имеется N сил, то результирующая сила вычисляется по правилу:
§4. Состояние физической системы. В физике существует понятие «состояние системы». Это понятие вводится не только в механике, но и в статистической физике, термодинамике, квантовой механике и т.д. Естественно, что в различных разделах физики это понятие обладает специфическими чертами. В механике термин «состояние» подразумевает, что для материальной точки для данного момента времени Если имеется система
Видно, что это выражение содержит всего В других разделах физики состояние системы определяется. Например, для твердых тел надо указывать не координаты ми скорости, а координаты и скорости центра масс и угловые скорости (см. ниже) вращения тела вокруг центра масс. В термодинамике идеальных газов состояние указывается термодинамическими потенциалами, к которым относится объем системы, её абсолютная температура и занимаемый системой объем, В квантовой механике указание состояния системы сложнее. Важность представления о состоянии системы определяется тем, что это понятие связано с основной задачей механики. Последняя решена, если есть указание на то, как состояние системы в момент времени
Законы Ньютона. В той или иной форме законы классической механики известны очень давно. Иногда эти законы формулировались и понимались с ошибками. Ярким примером одной из ошибок было неправильное понимание причин движения, высказанное Аристотелем. Он считал, что движение продолжается только до того момента времени, пока на объект действует сила. Ошибка состояла в том, что Аристотель не учитывал свойств инерции, присущих веществу. По мере развития физики и накопления экспериментальных данных, законы механики уточнялись и, наконец, были в современной форме сформулированы Исааком Ньютоном. Именем Ньютона названо много законов. Если говорить только о механике, то можно указать 4 закона Ньютона. Один из них – знаменитый закон Всемирного тяготения
Здесь Однако, говоря о законах Ньютона в механике, чаще подразумевают три закона. Первый закон – закон инерции. Как и остальные законы Ньютона он является результатом обобщения экспериментальных данных. Закон утверждает следующее. Если результирующая всех сил, действующих на материальную точку, равна нулю, то материальная точка находится в состоянии покоя или равномерного прямолинейного движения. Первый закон исправляет ошибку Аристотеля. Он утверждает, что в природе существуют инерциальные системы отсчета, относительно которых материальная точка может покоиться. Второй закон Ньютона, который иначе называется законом движения в классической физике может быть записан в трех близких формах: А).
Б).
В). Форма закона А) - наиболее примитивная, «школьная» форма Второго закона Ньютона. Она плоха тем, что глядя на неё можно подумать, что ускорение является постоянной величиной. На самом деле ускорение может изменяться с течением времени. Вторая форма – наиболее распространенная запись Второго закона Ньютона. Эту форму называют еще «Уравнение движения». Она дает решение для переменного ускорения или, что важнее, при заданных силах – зависимость Определение закона движения (выполняется двойным интегрированием по времени) составляет прямую основную задачу динамики. Определение равнодействующей силы по известному (например, из эксперимента) закону движения – обратная основная задача динамики. Приведем пример решения прямой задачи движения. Она имеет однозначное решение, если только заданы начальные условия, то есть координаты и проекции скоростей материальной точки в начальный момент времени (обычно за такой момент принимают Пусть сила, действующая на материальную точку, равна
или, используя определение мгновенного ускорения,
Отсюда следует
Если теперь провести неопределенное интегрирование, то можно получить
По условию, интеграл от силы существует, а значение скорости в начальный момент равно
Теперь, при заданной силе, мгновенная скорость полностью определена и можно переходить к определению закона движения. Для этого воспользуемся определением мгновенной скорости и запишем
Отсюда следует:
Опять проводим неопределенное интегрирование:
Первый интеграл вычисляется, давая
Закон движения определен полностью. Это называется решением первой задачи динамики «в квадратурах». Необходимо подчеркнуть, что первая задача динамики (для любого случая – прямолинейного движения или вращения, отдельной материальной точки, системы точек или твердого тела) может быть решена только при указании начальных условий. Форма В) – наиболее общая форма записи Второго закона Ньютона. Там проводится дифференцирование импульса по времени. Это дифференцирование может затрагивать только скорость, но может затрагивать и скорость, и массу. Такое дифференцирование пригодно и для релятивистских задач, когда масса зависит от скорости и от времени: Последнее утверждение получается при использовании двух других законов – Третьего закона Ньютона или закона сохранения импульса. Интересно, что в отличие от основных законов физики, являющихся (как правило) обобщением опытных данных, из закона сохранения импульса можно строго математически получить Третий закон Ньютона, и наоборот, приняв Третий закон можно на его основе получить закон сохранения импульса. Для того, чтобы сформулировать третий закон, надо ввести понятие «замкнутая система»(иногда говорят «изолированная система», см. Д.В. Сивухин, т. I Механика). По определению это такая система, на каждую материальную точку не действуют внешние силы. Тела замкнутой системы могут взаимодействовать только меду собой. Пусть система состоит из двух материальных точек. Тогда можно показать (или принять как экспериментальный факт), что эти силы имеют три особенности. Они: А) равны по величине (по модулю), Б) направлены вдоль прямой, соединяющей материальные точки, В) причем в противоположные стороны. Это словесная формулировка Третьего закона Ньютона. В виде формулы этот закон записывается так:
индекс Если система состоит из
Здесь есть некая тонкость, заключающаяся в том, что в механике рассматривают только парные взаимодействия частиц. Например, силы типа
Закон сохранения импульса. В §3 мы ввели понятие импульса материальной точки как величины, равной
Продифференцируем эту сумму по времени и учтем, что производная импульса есть сила:
Здесь
Если же система замкнута, то
Это математическая формулировка закона сохранения полного импульса замкнутой системы материальных точек. «Полный импульс замкнутой системы материальных точек не зависит от времени, то есть сохраняется». Задачи, для решения которых применяется закон сохранения полного импульса, достаточно известны. В частности ранее утверждалось, что если на корме небольшой лодки поставить вентилятор, который будет дуть в парус, то лодка останется неподвижной. Это не всегда так и опыты подтверждают это. Так, если не весь поток воздуха будет попадать на парус, то часть импульса проходящего мимо паруса не будет компенсировать силу отдачи и лодка начнет двигаться кормой вперед. Похожий эффект возникает, если молекулы воздуха упруго отражаются от паруса. Тогда импульсы и силы перераспределяются в пространстве, что создает отличную от нуля внешнюю силу. Картина в целом напоминает случаи рассеяния света на поглощающей и отражающей поверхностях.
Работа механической силы. А). Работа постоянной силы при прямолинейном перемещении; сила и перемещение S совпадают по направлению. Согласно определению, работой в этом случае называется произведение Б). Если вектор силы и вектор прямолинейного перемещения составляют угол Случаи А) и В) рассмотрены для постоянной по величине и направлению силы. В). Если же сила непостоянна по времени или направлению, то надо брать очень маленькие перемещения Г). Полная работа произвольной силы при перемещении по прямой L от начальной точки а до конечной точки в равна определенному интегралу
Д). Не всегда перемещение происходит по прямой линии. В этом случае рассматривают кривую линию с начальной точкой а и конечной точкой в,
Этот интеграл даёт наиболее общее выражение для работы произвольной силы. Е). Есть еще один случай работы силы, который надо упомянуть. Это работа по замкнутой траектории. В этом случае обозначается кружком на знаке криволинейного интеграла:
Здесь начало и конец кривой (траектории) совпадают и их не отмечают. Такие интегралы (мы их вычисляем для простейших случаев, когда вычисления очевидны и легки) крайне важны. Мы обсудим их значение позже, а пока отметим, что в том случае, когда
сила называется консервативной, а работа равна нулю независимо от выбора замкнутого контура. Примерами служат сила упругости, сила тяжести, сила Кулона и др. Если же
то сила называется неконсервативной. Её работа зависит от вида траектории L. Это силы трения (сухого и вязкого) силы необратимых деформаций др. С понятием «работа» связано понятие «мощность». Мощность – это работа, совершаемая в единицу времени или «скорость» совершения работы:
Мощность Р – скаляр, не путать с модулем импульса.
Потенциальная энергия. Как было отмечено, потенциальная энергия – это величина, показывающая, какую работу может совершить механическая система. Причем эта работа связана с массой и скоростью материальной точки. Другой тип механической энергии – это потенциальная энергия. Она менее универсальна, чем кинетическая энергия и проявляется не всегда. Одна из важных особенностей потенциальной энергии состоит в том, что она всегда определяется с точностью до произвольной постоянной. Работа, которую совершает система с потенциальной энергией, равна разности потенциальной энергии в начальном и конечном состояниях. Приведем несколько примеров. Пусть материальная точка массой m находится на высоте h над горизонтальной поверхностью. Тогда говорят, что её потенциальная энергия равна Подобным же образом потенциальной энергией обладает материальная точка на пружине, жесткость которой равна k. В самом деле, при небольших растяжениях пружины
Если пружину растягивать (заметим, что перемещения конца пружины противоположно по направлению действующей силы, что приводит к замене знака «–» на знак «+»), то совершаемая над пружиной работа, равная запасенной потенциальной энергии, составит
Полная потенциальная энергия определяется неопределенным интегралом, то есть равна
Произвольная постоянная может быть задана, если указать начало системы отсчета. Если конец нерастянутой пружины совпадает с началом отсчета, то константу принимают за нуль. Потенциальная энергия связана с силой, действующей на систему. Рассматривая движение только вдоль оси Х, легко установить, что
или, точнее,
Обобщение последней формулы на трехмерное движение дает
Выражения, стоящие справа (без учета знака «–») называют оператором набла,
Гармонический осциллятор. Рассмотрим простую физическую систему – материальную точку, которая без трения колеблется на горизонтальной поверхности под действием силы Гука (см. рис. 2).
Если смещение груза много меньше, чем длина недеформированной пружины, а жесткость пружины равна k, то но груз действует единственная сила, сила Гука. Тогда уравнение движения груза (Второй закон Ньютона) имеет вид
Перенеся слагаемые в левую часть равенства, и разделив на массу материальной точки m (массой пружины пренебрегаем по сравнению с m), получим уравнение движения
где
и
есть циклическая частота и период колебаний. Тогда, взяв функцию
и продифференцировав её по времени, убеждаемся, что скорость движения груза равна
а после повторного дифференцирования ускорение
то есть X(t) действительно является решением уравнения груза на пружинке. Рассмотренная система, вообще любая система, механическая, электрическая или иная, обладающая уравнением движения (*), называется гармоническим осциллятором. Функция типа X(t) носит название закона движения гармонического осциллятора; величины Закон движения X(t) представляет собой свободные колебания. Такие колебания совершают незатухающие маятники (математический или физический), ток и напряжения в идеальном колебательном контуре и некоторые другие системы. Гармонические колебания могут складываться в одном, или в различных направлениях. Результатом сложения тоже оказывается гармоническое колебание, например,
Это принцип суперпозиции (наложения) колебаний. Математики разработали теорию рядов такого рода, которые называются рядами Фурье. Имеется также ряд обобщений типа интегралов Фурье (частоты могут меняться непрерывным образом) и даже интегралы Лапласа, работающие с комплексными частотами.
Элементы механики жидкости. Три агрегатных состояния вещества газ, твердое тело и жидкость отличаются друг от друга величиной силового взаимодействия входящих в них элементов. В газах взаимодействие атомов и молекул не велико и газы занимают весь выделенный для них объем. Существует хорошо развитая кинетическая теория газов, частично рассматриваемая ниже. Теория твердых тел наиболее развитая часть квантового описания упорядоченных структур. Атомы в твердых телах «сильно» взаимодействуют друг с другом, что объясняет упругость и неизменность формы таких тел. Детальное изучение этих вопросов выпадает из данной части курса физики. Наименее развита теория жидкостей. Жидкость занимает часть выделенного для неё объема, что означает большую силу взаимодействия между частицами, чем у газов, но меньшую, чем между частицами твердых тел. Основа теории жидкостей (по современным представлениям) – это взаимодействие кластеров. Кластеры – объединение частиц (молекул), из которых состоит жидкость, их взаимодействие друг с другом и с окружающей средой. Кластеры содержат разное число частиц и имеют различные формы, что является одной из основных трудностей теорий жидкостей. Вместе с тем жидкости изучались давно и многие их свойства хорошо известны из опытов. При этом для объяснения наблюдений делают довольно сильные предположения. Одно из них – введение понятия несжимаемой жидкости. Это жидкость, объем или плотность которой не зависят от внешнего давления. В то же время такая жидкость не растягивается. Не будем обсуждать технические применения таких жидкостей (гидротормоза, гидроустройства станков и самолетов, измерительные устройства и т.д.). Отметим только, что в этой модели используется предположение о том, что межмолекулярные силы взаимодействий в жидкостях намного больше, чем в газах. Одновременно используются представления об идеальной жидкости. В этой жидкости, напротив, полностью пренебрегают взаимодействием частиц друг с другом. Говорят также, что идеальная жидкость такова, что в ней отсутствует вязкость или силы внутреннего трения. Неидеальная жидкость – случай, когда внутренним трением пренебречь нельзя. В отличие от настоящих твердых тел (кристаллов) жидкости текут. В объеме V, занятом жидкостью, можно ввести поле скоростей. Это означает, что каждая точка объема V характеризуется вектором скорости, с которой перемещается бесконечно малый объем жидкости. Другими словами, вводят функцию
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1543; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.19.206 (0.012 с.) |

 . Тогда положение данной точки пространства однозначно указывается радиус-вектором, например,
. Тогда положение данной точки пространства однозначно указывается радиус-вектором, например,  , где
, где  – проекции координат точки на соответствующие оси. Если точка движется, то радиус-вектор становится функцией времени.
– проекции координат точки на соответствующие оси. Если точка движется, то радиус-вектор становится функцией времени. прямолинейного движения называется отношение
прямолинейного движения называется отношение (м/с).
(м/с). .
.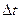 . Если рассматривать предел отношения при
. Если рассматривать предел отношения при  , то есть заменить отношение производной, то можно ввести мгновенную скорость в момент времени t:
, то есть заменить отношение производной, то можно ввести мгновенную скорость в момент времени t: ,
, 
 .
. (м/с2).
(м/с2). ,
, – произвольный постоянный вектор,
– произвольный постоянный вектор,  – некоторые постоянные числа, связанные с Х, У и Z проекциями,
– некоторые постоянные числа, связанные с Х, У и Z проекциями, 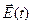 – некоторая функция времени. Размерности перечисленных величин таковы, что вся правая часть имеет линейную размерность.
– некоторая функция времени. Размерности перечисленных величин таковы, что вся правая часть имеет линейную размерность. .
. .
.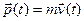 .
. .
. .
. .
. полный импульс и полная энергия системы при некоторых дополнительных условиях может сохраняться во времени.
полный импульс и полная энергия системы при некоторых дополнительных условиях может сохраняться во времени.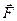 .
. .
. .
. известны или указаны три координаты
известны или указаны три координаты  . Обратим внимание на то, что «три» – это число пространственных переменных или, что важнее, число степеней свободы.
. Обратим внимание на то, что «три» – это число пространственных переменных или, что важнее, число степеней свободы. невзаимодействующих материальных точек, то для определения состояния системы в момент времени
невзаимодействующих материальных точек, то для определения состояния системы в момент времени  проекций координат и проекций скоростей. То есть для момента времени
проекций координат и проекций скоростей. То есть для момента времени  ,
,  .
. элементов; индекс
элементов; индекс  отображает номер рассматриваемой материальной точки. Если точки взаимодействуют между собой (пусть число таких взаимодействий равно
отображает номер рассматриваемой материальной точки. Если точки взаимодействуют между собой (пусть число таких взаимодействий равно  ), то число степеней свободы равняется
), то число степеней свободы равняется 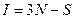 , то есть число указываемых проекций координат уменьшается и равно
, то есть число указываемых проекций координат уменьшается и равно  .
. .
. ,
,  – бесконечно малое превращение времени. Очевидно, что если такое указание найдено, то движение системы описано полностью для любых времен. Ньютон нашел универсальный способ решения этой проблемы, записав «уравнение движения системы» (см. следующий параграф).
– бесконечно малое превращение времени. Очевидно, что если такое указание найдено, то движение системы описано полностью для любых времен. Ньютон нашел универсальный способ решения этой проблемы, записав «уравнение движения системы» (см. следующий параграф). .
. – постоянная Всемирного тяготения,
– постоянная Всемирного тяготения, 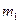 и
и  – взаимодействующие массы, расстояние между которыми равно
– взаимодействующие массы, расстояние между которыми равно  , дробь
, дробь  – орт, указывающий направление действия силы и проведенный из первой массы, знак минус показывает, что при взаимодействии масс возникает сила притяжения.
– орт, указывающий направление действия силы и проведенный из первой массы, знак минус показывает, что при взаимодействии масс возникает сила притяжения. .
. .
. .
. , которую называют «Закон движения».
, которую называют «Закон движения». , но можно выбирать произвольное значение
, но можно выбирать произвольное значение  ).
). и дважды интегрируема. Пусть также начальное положение точки определяется условием
и дважды интегрируема. Пусть также начальное положение точки определяется условием  , а начальная скорость – условием
, а начальная скорость – условием  . Учитывая Второй закон Ньютона, найдем:
. Учитывая Второй закон Ньютона, найдем: ,
, .
. .
. .
. . Так как сила в начальный момент еще не изменила скорость, то мгновенная скорость приобретает однозначный вид
. Так как сила в начальный момент еще не изменила скорость, то мгновенная скорость приобретает однозначный вид .
. .
. .
. .
. , второй остается неизменным – в случае конкретного указания силы, он также может быть вычислен. Произвольная константа определяется по начальному условию. При
, второй остается неизменным – в случае конкретного указания силы, он также может быть вычислен. Произвольная константа определяется по начальному условию. При  и тогда
и тогда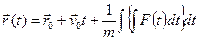 .
. . Эта же форма пригодна и для классической области, если масса системы переменна. Примерами может служить поливальная машина и ракета. Именно на основе этой формы Циолковский получил уравнение движения ракеты и обосновал утверждение, что ракета может лететь в вакууме (было время, когда некоторые ученые утверждали, что в космосе ракета не полетит: «Ей там не от чего отталкиваться»).
. Эта же форма пригодна и для классической области, если масса системы переменна. Примерами может служить поливальная машина и ракета. Именно на основе этой формы Циолковский получил уравнение движения ракеты и обосновал утверждение, что ракета может лететь в вакууме (было время, когда некоторые ученые утверждали, что в космосе ракета не полетит: «Ей там не от чего отталкиваться»).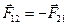 ,
,  показывает, что рассматривается сила, действующая на первую материальную точку со стороны второй точки.
показывает, что рассматривается сила, действующая на первую материальную точку со стороны второй точки. .
. и более сложные не рассматриваются.
и более сложные не рассматриваются. .
. .
. и
и  – силы, действующие со стороны второй и третьей материальной точки на первую точку,
– силы, действующие со стороны второй и третьей материальной точки на первую точку,  и
и  а – силы, действующие со стороны первой точки на вторую и третью. Вследствие Третьего закона Ньютона они попарно сокращаются. Также попарно сокращаются все внутренние силы, действующие в систем е материальных точек. Остается только
а – силы, действующие со стороны первой точки на вторую и третью. Вследствие Третьего закона Ньютона они попарно сокращаются. Также попарно сокращаются все внутренние силы, действующие в систем е материальных точек. Остается только  – результирующая или равнодействующая сил, действующих на систему материальных точек извне:
– результирующая или равнодействующая сил, действующих на систему материальных точек извне: .
. .
. . Размерность работы, как и энергии, равна Дж (или Н).
. Размерность работы, как и энергии, равна Дж (или Н). , то работа равна
, то работа равна  . Например,
. Например,  . Здесь
. Здесь  – обозначение скалярного произведения двух векторов.
– обозначение скалярного произведения двух векторов. , на протяжении которых сила не меняется. Тогда можно ввести понятие элементарной работы,
, на протяжении которых сила не меняется. Тогда можно ввести понятие элементарной работы, 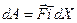 , или, в более общем виде
, или, в более общем виде 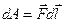 ,
,  – элементарное (бесконечно малое) а значит – прямолинейное смещение.
– элементарное (бесконечно малое) а значит – прямолинейное смещение. .
. , и определенное интегрирование проводят по малым (прямолинейным) отрезкам этой кривой. Такой определенный интеграл называется криволинейным и обозначается как
, и определенное интегрирование проводят по малым (прямолинейным) отрезкам этой кривой. Такой определенный интеграл называется криволинейным и обозначается как .
. .
. ,
, ,
, .
. , где g – ускорение свободного падения при данных условиях. При этом мы могли бы проводить отсчет «высоты», скажем, от потолка комнаты. Независимо от этого и вне зависимости от вида траектории, по которой падает материальная точка (свободное падение, без трения), работа совершаемая силой тяжести одинакова и равна
, где g – ускорение свободного падения при данных условиях. При этом мы могли бы проводить отсчет «высоты», скажем, от потолка комнаты. Независимо от этого и вне зависимости от вида траектории, по которой падает материальная точка (свободное падение, без трения), работа совершаемая силой тяжести одинакова и равна  , где
, где 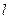 – длина недеформированной пружины можно записать силу Гука
– длина недеформированной пружины можно записать силу Гука .
. .
. .
. ,
, .
. .
. , или оператором градиент,
, или оператором градиент,  , или просто записывают в виде
, или просто записывают в виде  . Все эти обозначения эквивалентны. Использование «круглых» символов
. Все эти обозначения эквивалентны. Использование «круглых» символов  и подобных им показывает, что производная вычисляется при фиксированных значениях остальных пространственных переменных, то есть вычисляется частная производная.
и подобных им показывает, что производная вычисляется при фиксированных значениях остальных пространственных переменных, то есть вычисляется частная производная.

 (*),
(*),
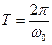

 ,
, ,
, называются амплитудой, циклической или собственной частотой, начальной фазой гармонического осциллятора. Частота определяется параметрами осциллятора, амплитуда и начальная фаза задаются начальными условиями.
называются амплитудой, циклической или собственной частотой, начальной фазой гармонического осциллятора. Частота определяется параметрами осциллятора, амплитуда и начальная фаза задаются начальными условиями. .
. . Если поле скоростей не зависит от времени, т.е.
. Если поле скоростей не зависит от времени, т.е.  , то говорят, что течение является установившимся или стационарным. При отсутствии внешних сил стационарно может двигаться только идеальная жидкость. В противном случае силы внутреннего трения при
, то говорят, что течение является установившимся или стационарным. При отсутствии внешних сил стационарно может двигаться только идеальная жидкость. В противном случае силы внутреннего трения при 


