
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое описание ансамбля частиц.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В основе статистического описания лежат представления о вероятностях (если события дискретные) и функций распределения вероятностей или плотностях вероятностей (для событий, меняющихся непрерывно). С вероятностями мы встречаемся постоянно, если рассматриваем случайные процессы. Эти понятия интуитивны. Ясно, что падение листа с дерева осенью – случайный процесс. Напротив, осенний листопад – закономерное, неслучайное явление. Чаще всего граница между этими категориями событий определяется экспериментально. Можно сказать, что случайный процесс – это явление, причины которого нам (пока) неизвестны. Стандартные примеры случайных процессов – падение монеты той или иной стороной, или падение кубика вверх одной из цифр от 1 до 6. Эти примеры позволяют указать вероятности тех или иных событий. Рассмотрим падение монеты. То, что она упадет – достоверное событие, вероятность которого равна единице. А тот факт, что она упадет предсказанной стороной вверх, происходит с вероятностью 0,5. Это проверяется экспериментально. Так, если бросить монету 1000 раз, то появление каждой из сторон произойдет примерно в 500 случаях. Отклонение от числа 500 случаев возможно на незначительную величину, которая называется дисперсией случайной величины или её флуктуацией. Если стремить число бросков «к бесконечности», вероятность появления заданной стороны станет равным 0,5. Аналогичным образом бросание кубика большое число раз даст вероятность появления любой грани равной Если вспомнить о мешке с черными и белыми шарами, то для предсказания того, какого цвета будет вынутый шар, надо учесть, сколько таких шаров в мешке. Поскольку вероятность того, что какой-либо шар вынут, равна 1, то можно записать равенство
Здесь индекс 1 соответствует вероятности появления белого шара, индекс 2 – появления черного (или наоборот). Кстати, приведенное равенство называется условием нормировки вероятностей. Но по аналогии с кубиком, вероятность достать белый шар равна
где Рассмотрим случайную величину, изменяющуюся непрерывно. Обозначим её как
Чтобы от пропорции перейти к равенству, надо вставить в правую часть скалярную функцию от аргумента Х:
Функция Функция распределения нормируется условием
Такая нормировка называется нормировкой на единицу. Если в системе имеется Средние статистические величины от переменной Х вычисляются следующим образом. Вначале записывают тождество
Интегрирование проводится по всем допустимым значениям Х. Затем предполагается, что в первом интеграле стоит не сам оператор
Поскольку функция распределения предполагается нормированной на единицу, стоящий слева интеграл равен 1 и мы получает формулу для расчета среднего
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 444; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.165.228 (0.007 с.) |

 . Разумеется, для этого грани кубика должны быть одинаковыми. Строго говоря, если цифры обозначены углублениями, то грань 1 немного тяжелее грани 6 и поэтому появление цифры 1 немного больше
. Разумеется, для этого грани кубика должны быть одинаковыми. Строго говоря, если цифры обозначены углублениями, то грань 1 немного тяжелее грани 6 и поэтому появление цифры 1 немного больше  .
. ,
, – число одинаковых белых шаров,
– число одинаковых белых шаров,  – число черных шаров.
– число черных шаров.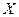 . Будем считать, что Х может изменяться от А до В. Тогда вероятность
. Будем считать, что Х может изменяться от А до В. Тогда вероятность  найти Х в диапазоне
найти Х в диапазоне  будет пропорциональна
будет пропорциональна  (если охватывается весь диапазон
(если охватывается весь диапазон  , то, очевидно, вероятность должна равняться 1; это опять условие нормировки вероятностей),
, то, очевидно, вероятность должна равняться 1; это опять условие нормировки вероятностей), .
. .
. называется функцией распределения или плотностью вероятности. Для нахождения её явного вида приходится использовать либо экспериментальные данные (феноменологический подход), либо строить некоторое кинетическое уравнение, решением которого служит
называется функцией распределения или плотностью вероятности. Для нахождения её явного вида приходится использовать либо экспериментальные данные (феноменологический подход), либо строить некоторое кинетическое уравнение, решением которого служит 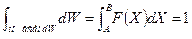 .
. одинаковых объектов, справа вместо 1 иногда ставят число
одинаковых объектов, справа вместо 1 иногда ставят число  , где
, где  – та физическая величина, которую надо сопоставлять с экспериментом, или функциональные зависимости которой от разных параметров надо исследовать. Тождество интегрируют с функцией распределения (оно остается тождеством):
– та физическая величина, которую надо сопоставлять с экспериментом, или функциональные зависимости которой от разных параметров надо исследовать. Тождество интегрируют с функцией распределения (оно остается тождеством): .
.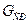 , которое является независящей от Х константой. Константу вынести из под интеграла,
, которое является независящей от Х константой. Константу вынести из под интеграла,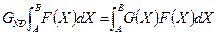 .
. .
.


