
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения момента импульса. Кинетическая энергия твердого тела.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вернемся к векторной форме уравнения моментов. Из него видно, что момент импульса тела остается постоянным относительно выбранной неподвижной точки, если момент внешних сил относительно этой же точки равен нулю. Данная фраза представляет собой формулировку закона сохранения момента импульса. В математической записи этот закон формулируется так:
Итак, теперь мы знаем ТРИ закона сохранения в механике: закон сохранения импульса, закон сохранения полной механической энергии и закон сохранения момента импульса. Движущаяся материальная точка или система материальных точек имеют кинетическую энергию. А твердое тело? Положительный ответ на вопрос очевиден, но по каким формулам находить кинетическую энергию вращения? Рассмотрим материальную точку
Учтем, однако, что линейная скорость связана с угловой скоростью соотношением
Здесь
А если твердое тело и вращается вокруг оси, проходящей через центр масс, и движется прямолинейно со скоростью
Физический маятник и период его колебаний. Определим, в качестве простого примера, период колебаний физического маятника или твердого тела (см. рис. 6). На рисунке 6 овал – рассматриваемое твердое тело, способное без трения качаться около горизонтальной оси, проходящей через точку О, не совпадающую с центром масс А. Момент инерции тела относительно указанной оси известен и равен J. К центру масс тела приложена сила тяжести. В некоторый момент времени маятник отклонен от вертикали на небольшой угол
Слева стоит вторая производная по времени от угла отклонения Принципиально важным обстоятельством является тот факт, что внешний момент оказывается возвращающим. Это означает, что вне зависимости от направления движения твердого тела (линии ОВ) – вправо или влево, и вне зависимости от того, находится ли центр масс слева от вертикали ОС или справа, момент силы тяжести стремится вызвать движение тела к положению равновесия, к линии ОС. Поэтому справа появляется знак «–». Тогда уравнение движения принимает вид
Рассматриваются малые углы отклонения маятника, поэтому можно приближенно считать, что
то есть к уравнению движения гармонического осциллятора с собственной частотой
Соответственно период колебаний равен:
Приведенная длина физического маятника, период колебаний которого равен периоду колебаний некоторого физического маятника. Заметим, что закон движения физического маятника имеет вид
Амплитуда и начальная фаза колебаний определяются двумя начальными условиями
А и В - заданные постоянные.
Элементы механики жидкости. Три агрегатных состояния вещества газ, твердое тело и жидкость отличаются друг от друга величиной силового взаимодействия входящих в них элементов. В газах взаимодействие атомов и молекул не велико и газы занимают весь выделенный для них объем. Существует хорошо развитая кинетическая теория газов, частично рассматриваемая ниже. Теория твердых тел наиболее развитая часть квантового описания упорядоченных структур. Атомы в твердых телах «сильно» взаимодействуют друг с другом, что объясняет упругость и неизменность формы таких тел. Детальное изучение этих вопросов выпадает из данной части курса физики. Наименее развита теория жидкостей. Жидкость занимает часть выделенного для неё объема, что означает большую силу взаимодействия между частицами, чем у газов, но меньшую, чем между частицами твердых тел. Основа теории жидкостей (по современным представлениям) – это взаимодействие кластеров. Кластеры – объединение частиц (молекул), из которых состоит жидкость, их взаимодействие друг с другом и с окружающей средой. Кластеры содержат разное число частиц и имеют различные формы, что является одной из основных трудностей теорий жидкостей. Вместе с тем жидкости изучались давно и многие их свойства хорошо известны из опытов. При этом для объяснения наблюдений делают довольно сильные предположения. Одно из них – введение понятия несжимаемой жидкости. Это жидкость, объем или плотность которой не зависят от внешнего давления. В то же время такая жидкость не растягивается. Не будем обсуждать технические применения таких жидкостей (гидротормоза, гидроустройства станков и самолетов, измерительные устройства и т.д.). Отметим только, что в этой модели используется предположение о том, что межмолекулярные силы взаимодействий в жидкостях намного больше, чем в газах. Одновременно используются представления об идеальной жидкости. В этой жидкости, напротив, полностью пренебрегают взаимодействием частиц друг с другом. Говорят также, что идеальная жидкость такова, что в ней отсутствует вязкость или силы внутреннего трения. Неидеальная жидкость – случай, когда внутренним трением пренебречь нельзя. В отличие от настоящих твердых тел (кристаллов) жидкости текут. В объеме V, занятом жидкостью, можно ввести поле скоростей. Это означает, что каждая точка объема V характеризуется вектором скорости, с которой перемещается бесконечно малый объем жидкости. Другими словами, вводят функцию Отмеченное выше свойство несжимаемости и нерастяжимости жидкости позволяют ввести уравнение неразрывности. Это одно из основных уравнений динамики течения жидкости. Выделим в поле скоростей некое сечение, перпендикулярное векторам движения (малый элемент Указанное уравнение или его модификация, например,
(интегрирование проводится по различным сечениям трубки тока,
где смысл оператора дивергенция определяется правилом
Это уравнение неразрывности (часто говорят «уравнение непрерывности») в отсутствие источников. Однако жидкость может дополнительно поступать или удаляться по каналу, пересекающему поверхность трубки тока. Тогда нуль в правой части уравнения заменяется известной для рассматриваемой системы функцией источников. До сих пор мы давали описание движения жидкости без учета энергетических соображений. Учет их позволяет найти основное для течения идеальной жидкости уравнение – уравнение Бернулли. Пусть на входе в трубку тока на жидкость оказывается давление Р1, а на выходе – давление Р2. Учтем также, что за время
Совершаемая над жидкостью работа равна
или, вводя давления
Далее, вводя объемы жидкости
Поэтому
Наконец стандартный вид известного уравнения Бернулли:
Пусть
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 660; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.53.112 (0.011 с.) |

 ..
.. , которая движется по окружности радиуса
, которая движется по окружности радиуса  с постоянной по модулю скоростью
с постоянной по модулю скоростью  . С точки зрения динамики материальной точки кинетическая энергия в этом случае равна
. С точки зрения динамики материальной точки кинетическая энергия в этом случае равна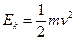 .
.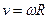 . Поэтому кинетическую энергию можно записать и в виде
. Поэтому кинетическую энергию можно записать и в виде .
. – момент инерции материальной точки относительно неподвижной оси вращения, а
– момент инерции материальной точки относительно неподвижной оси вращения, а  – угловая скорость её вращения относительно той же оси. Этот результат можно обобщить на случай любого твердого тела, вращающегося вокруг неподвижной оси, проходящей через центр масс:
– угловая скорость её вращения относительно той же оси. Этот результат можно обобщить на случай любого твердого тела, вращающегося вокруг неподвижной оси, проходящей через центр масс: .
. .
. . Для описания вращения тела вокруг оси можно записать уравнение движения
. Для описания вращения тела вокруг оси можно записать уравнение движения .
.
 . Справа – момент внешних сил, действующих на систему. Численно этот момент равен
. Справа – момент внешних сил, действующих на систему. Численно этот момент равен 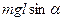 , где
, где  , то есть равняется расстоянию от оси вращения до центра масс, тогда как
, то есть равняется расстоянию от оси вращения до центра масс, тогда как  – плечо действующей силы.
– плечо действующей силы. .
. . В результате уравнение движения приводится к виду
. В результате уравнение движения приводится к виду ,
, .
. .
. .
.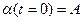 ,
, .
. . Если поле скоростей не зависит от времени, т.е.
. Если поле скоростей не зависит от времени, т.е.  , то говорят, что течение является установившимся или стационарным. При отсутствии внешних сил стационарно может двигаться только идеальная жидкость. В противном случае силы внутреннего трения приводят к нагреву и остановке движения жидкости.
, то говорят, что течение является установившимся или стационарным. При отсутствии внешних сил стационарно может двигаться только идеальная жидкость. В противном случае силы внутреннего трения приводят к нагреву и остановке движения жидкости. ,
,  – орт, нормальный к поверхности
– орт, нормальный к поверхности  ). Векторы скорости, проходящие через границу сечения, не пересекаются (жидкость не может «втечь сама в себя») и образуют трубку тока. Поскольку жидкость не может выйти из трубки тока, то в любом сечении трубки
). Векторы скорости, проходящие через границу сечения, не пересекаются (жидкость не может «втечь сама в себя») и образуют трубку тока. Поскольку жидкость не может выйти из трубки тока, то в любом сечении трубки  . При этом предполагается, что плотность жидкости постоянна (свойство несжимаемости). Можно убедиться, что равенство
. При этом предполагается, что плотность жидкости постоянна (свойство несжимаемости). Можно убедиться, что равенство  ,
, – плотность жидкости в данном сечении трубки) представляет собой одну из формулировок, определяющих трубку тока. Они могут считаться уравнениями неразрывности, но строгие определения – другие. Есть более общие формы уравнения неразрывности. Во-первых, дифференциальная форма, учитывающая, что плотность жидкости может зависеть от времени,
– плотность жидкости в данном сечении трубки) представляет собой одну из формулировок, определяющих трубку тока. Они могут считаться уравнениями неразрывности, но строгие определения – другие. Есть более общие формы уравнения неразрывности. Во-первых, дифференциальная форма, учитывающая, что плотность жидкости может зависеть от времени, ,
, .
.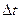 сечение на входе в трубку сместится на
сечение на входе в трубку сместится на  , а на выходе – на величину
, а на выходе – на величину  . Если умножить смещения на площадь поперечного сечения в соответствующем месте трубки и на плотность жидкости, то можно получить величину массы, прошедшей через начало и конец трубки тока. В силу непрерывности тока, эти массы равны. Обозначим их как
. Если умножить смещения на площадь поперечного сечения в соответствующем месте трубки и на плотность жидкости, то можно получить величину массы, прошедшей через начало и конец трубки тока. В силу непрерывности тока, эти массы равны. Обозначим их как  . Тогда, в силу закона сохранения механической энергии
. Тогда, в силу закона сохранения механической энергии  . то есть разность энергий на выходе и на входе в трубку тока равна работе, совершенной над жидкостью в трубке. Но, очевидно, что
. то есть разность энергий на выходе и на входе в трубку тока равна работе, совершенной над жидкостью в трубке. Но, очевидно, что ,
, .
. ,
, с помощью соотношений
с помощью соотношений  , учитывающих площади сечений трубки тока на входе и выходе,
, учитывающих площади сечений трубки тока на входе и выходе, .
. , находим
, находим .
. .
. .
. . Тогда там, где скорость движения жидкости меньше, там давление жидкости больше.
. Тогда там, где скорость движения жидкости меньше, там давление жидкости больше.


