
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределения Максвелла и Больцмана.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Первым распределением статистической физики было распределение частиц идеального газа. находящегося в равновесии, по скоростям. Оно было получено Максвеллом с помощью теории вероятностей и кинетических представлений. Максвелл нашел число частиц ансамбля, скорости которых лежат в интервале
где функция скорости называется функцией распределения Максвелла по скоростям. В силу независимости движений по осям координат, функцию распределения можно представить произведением функций
Максвелл доказал, что в одномерном случае
M – масса частицы, функции распределения на число частиц N
предполагается, что при тепловом (хаотическом) движении вдоль оси Х скорость частицы может принимать любые значения от Для определения константы нормировки
так что
после чего число частиц
и условие нормировки принимает вид
Здесь рассматривается «табличный» интеграл Френеля
и постоянная нормировки для одномерного движения приобретает вид
Теперь нормированную на число частиц функцию распределения Максвелла по скоростям в случае одномерного движения можно записать в виде
Позже это распределение было проверено экспериментально и получило хорошее подтверждение в опытах Штерна и Герлаха. Напомним, что рассматривалось одномерное движение. Для рассмотрения трехмерного движения надо вспомнить, что в силу независимости движения по ортогональным осям координат
и опять провести нормировку на число частиц:
Здесь перемножаются три одинаковых интеграла типа
так что новая постоянная нормировки
Значит, в случае трехмерного движения функция распределения Максвелла имеет вид
Уместно замечание о том, что в настоящее время чаще используют распределение не по скоростям, а по импульсам (тогда это распределение можно использовать в релятивистских задачах):
Эта функции распределения относится к случаю прямоугольной Декартовой системы координат. Однако часто удобнее использовать сферическую систему координат, считая, что
при этом по телесному углу
Функцию распределения по модулям скоростей можно изобразить графиком (см. рис. 9).
На рисунке 9 приближенное изображение функции распределения Максвелла для некоторой температуры T. Точка А – точка касания горизонтальной прямой – максимум функции При изучении распределения Максвелла по скоростям Больцман заметил, что в показателе экспоненты стоит отношение кинетической энергии к энергии
где нормировка проводится по всем координатам, либо по указанной координатной области. Например, если рассматривается изотермическая атмосфера, находящаяся в равновесии, и потенциальная энергия частиц ансамбля равна
где Z – высота над уровнем моря, то тогда
Нормировка может проводиться на плотность частиц в единице объема (на концентрацию частиц
Величины, имеющие индексы «0» – отмечают значения на уровне моря. Аналогичным образом можно записать распределение гармонических осцилляторов по энергиям. Если считать, что энергия осциллятора равна
то соответствующая функция распределения имеет вид
Дальнейшим обобщением функций распределения в классической статистической физике является распределение Максвелла – Больцмана, которое учитывает и пространственные, и скоростные переменные:
распределения зависит как от скорости, так и от координаты частицы (поскольку потенциальная энергия есть функция координат). Соответственно определяющие нормировку и используемые для вычисления интегралы учитывают как интегрирование по скоростям, так и по координатам (по всему фазовому пространству). Мы отмечали, что рассматривались равновесные ансамбли. Для теории технологических процессов, когда имеются интенсивные внешние воздействия на ансамбли, важны неравновесные функции распределения. Их приходится получать в отдельности для каждой физической (да и не только физической – химической, биологической, экономической и т.д.) системы. Это сложные современные задачи, имеющие большое экономическое значение. Кроме неравновесных функций распределения изучаются квантовые функции распределения. Наиболее известные квантовые распределения – это функции распределения Бозе-Эйнштейна и Ферми-Дирака. С их помощью строятся современные теории электропроводности, лазерной физики и многих других теорий.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 676; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.69.58 (0.006 с.) |

 . Это число можно записать в виде
. Это число можно записать в виде ,
, , что позволит вначале рассмотреть случай одномерного движения, например, вдоль оси Х. Тогда
, что позволит вначале рассмотреть случай одномерного движения, например, вдоль оси Х. Тогда , где
, где 
 ,
, – постоянная Больцмана, T – абсолютная температура ансамбля в кельвинах. А постоянная
– постоянная Больцмана, T – абсолютная температура ансамбля в кельвинах. А постоянная  определяется условием нормирования
определяется условием нормирования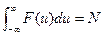 ,
, до
до  .
. ,
, ,
,
 .
. ,
, .
.
 .
. .
. .
.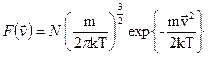 .
. .
. ,
, можно проинтегрировать, что дает множитель
можно проинтегрировать, что дает множитель  , и тогда
, и тогда  можно заменить множителем
можно заменить множителем  . Функция распределения в этом случае зависит от модуля скорости, изменяющемся в интервале
. Функция распределения в этом случае зависит от модуля скорости, изменяющемся в интервале  . Такая функция называется функцией распределения Максвелла по модулям скоростей и имеет вид
. Такая функция называется функцией распределения Максвелла по модулям скоростей и имеет вид .
.
 . Этой точке соответствует наиболее вероятная скорость. Площадь под кривой определяет условие нормировки (1 или N). При повышении температуры максимум сдвигается вправо, становясь ниже, так что нормировка и площадь под кривой сохраняются.
. Этой точке соответствует наиболее вероятная скорость. Площадь под кривой определяет условие нормировки (1 или N). При повышении температуры максимум сдвигается вправо, становясь ниже, так что нормировка и площадь под кривой сохраняются. . Это послужило основанием для обобщения распределения на случай, когда частица имеет потенциальную энергию. Такое распределение часто называют распределением Больцмана. В этом случае функция распределения может быть записана в виде
. Это послужило основанием для обобщения распределения на случай, когда частица имеет потенциальную энергию. Такое распределение часто называют распределением Больцмана. В этом случае функция распределения может быть записана в виде ,
, ,
, .
. ) или на давление P(Z). Тогда говорят о барометрических распределениях, имеющих вид
) или на давление P(Z). Тогда говорят о барометрических распределениях, имеющих вид ,
, .
. ,
, .
. .
.


