
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение Максвелла по абсолютным значениям скорости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Разбиение вероятности
где
Элемент объема
Вероятность молекулы иметь кинетическую энергию от K 1 до K 1 + dK 1, обладая при этом определенными проекциями импульсов, равна
Аналогично, вероятность молекулы иметь кинетическую энергию от K 1 до K 1 + dK 1, обладая при этом определенными проекциями скорости, равна
Фазовый объем, соответствующий кинетической энергии, лежащей в диапазоне от K 1 до K 1 + dK 1 при всех возможных импульсах или скоростях, определяется шаровым слоем
В пространстве скоростей
Постоянную А найдем из условия нормировки Пользуясь табличным интегралом Пуассона -
Формула (2.22) дает вероятность того, что скорость молекулы лежит в диапазоне от v до v + dv, т.е. в шаровом слое пространства скоростей. Свойства распределения Максвелла: 1) Плотность вероятности
Рис.2.2. Распределение Максвелла по абсолютным значениям скорости. Максимум получается при скорости, которая и называется наиболее вероятной скоростью
2) Полная площадь под кривой f (v) равна 1, поскольку она равна нормировочному интегралу. Интерпретация участка заштрихованной площади под кривой: площадь заштрихованной области равна вероятности того, что скорость молекулы в диапазоне от v до v + dv. Для вероятности получить скорость молекул в конечном интервале скоростей необходимо вычислить
3) Распределение вероятностей зависит от температуры. На рисунке 2.3 представлено несколько кривых f (v) при разных температурах.
Рис.2.3. Распределение Максвелла при разных температурах.
С ростом температуры диапазон скоростей все расширяется, а наиболее вероятная скорость сдвигается в область больших скоростей ( Характерные средние скорости: 1) Средняя скорость. По определению
Произведем замену переменных:
2) Средняя квадратичная скорость. По определению, среднее значение квадрата скорости
В нашем случае
И средняя квадратичная скорость равна
Отсюда можно получить среднюю кинетическую энергию, приходящуюся на молекулу:
(2.30)
Рис.2.4. Характерные скорости распределения Максвелла.
На графике функции распределения
Из Рис.2.4. видно, что максимум функции распределения довольно широк. Это отражает большой разброс в абсолютных значениях скоростей молекулы, т.е. большие флуктуации её скорости. Одна молекула - подсистема, которая содержит малое число частиц, поэтому флуктуации велики;
3) Для подсистемы с N частицами её полная кинетическая энергия
Из этих N частиц доля молекул, имеющих скорости от от v до v + dv, в силу независимости будет равна
Эта вероятность имеет очень резкий максимум как функция скорости v, при этом функция распределения по скоростям в системе
Рис.2.5. Распределение Максвелла для N частиц.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 748; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

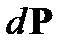 на произведение вероятностей
на произведение вероятностей  позволяет найти распределение молекул газа по абсолютным значениям скоростей. Пусть система состоит из большого числа невзаимодействующих молекул. Кинетическая энергия системы
позволяет найти распределение молекул газа по абсолютным значениям скоростей. Пусть система состоит из большого числа невзаимодействующих молекул. Кинетическая энергия системы  , где
, где  - кинетическая энергия молекулы. Соответствующий фазовый объем равен
- кинетическая энергия молекулы. Соответствующий фазовый объем равен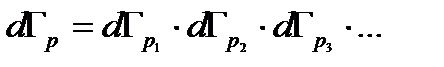 Поскольку все частицы одинаковы и каждую из них можно рассматривать, как независимую подсистему, то вероятность имеет вид произведения
Поскольку все частицы одинаковы и каждую из них можно рассматривать, как независимую подсистему, то вероятность имеет вид произведения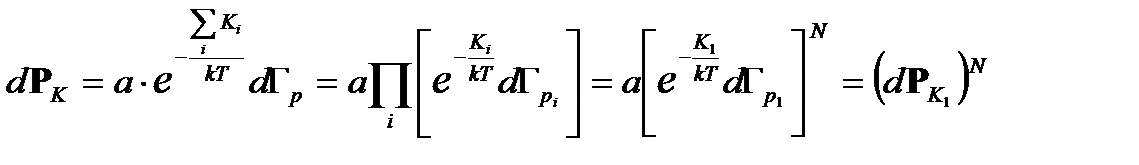 , (2.14)
, (2.14) - пропорциональна распределению вероятностей по абсолютным значениям скоростей каждой отдельной молекулы:
- пропорциональна распределению вероятностей по абсолютным значениям скоростей каждой отдельной молекулы: (2.15)
(2.15) . Итак, функция распределения вероятностей по кинетическим энергиям для одной молекулы имеет вид
. Итак, функция распределения вероятностей по кинетическим энергиям для одной молекулы имеет вид (2.16)
(2.16)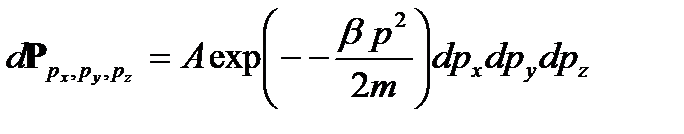 (2.17)
(2.17) (2.18)
(2.18)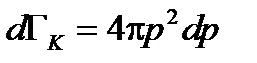 или
или  . Вероятность иметь кинетическую энергию от K 1 до K 1 + dK 1 при всех возможных импульсах равна
. Вероятность иметь кинетическую энергию от K 1 до K 1 + dK 1 при всех возможных импульсах равна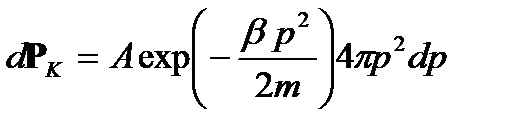 (2.19)
(2.19)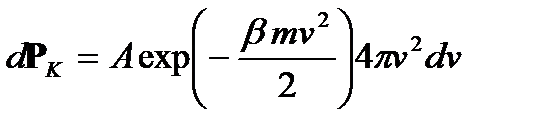 (2.20)
(2.20) .
. , получаем:
, получаем: , (2.21)
, (2.21)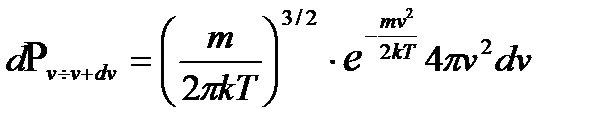 . (2.22)
. (2.22) , имеет максимум при некоторой скорости v молекул. Из (2.22) следует, что при малых скоростях вероятность растет пропорционально v 2 из-за фазового объема, а далее с ростом скорости v функция резко убывает из-за экспоненциального множителя. Найдем наиболее вероятную скорость, т.е. скорость, при которой имеется максимум функции f (v). Так как
, имеет максимум при некоторой скорости v молекул. Из (2.22) следует, что при малых скоростях вероятность растет пропорционально v 2 из-за фазового объема, а далее с ростом скорости v функция резко убывает из-за экспоненциального множителя. Найдем наиболее вероятную скорость, т.е. скорость, при которой имеется максимум функции f (v). Так как  , то, приравнивая нулю её производную, получаем
, то, приравнивая нулю её производную, получаем 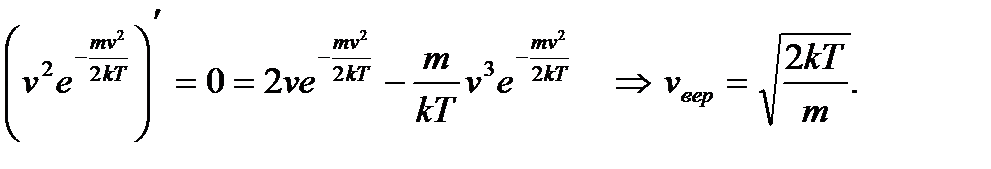
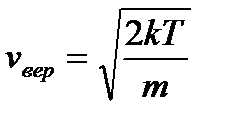 ; (2.23)
; (2.23) ; (2.24)
; (2.24)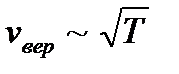 ), при этом наиболее вероятной скоростью обладают все меньшее число молекул(максимум становится меньше).
), при этом наиболее вероятной скоростью обладают все меньшее число молекул(максимум становится меньше).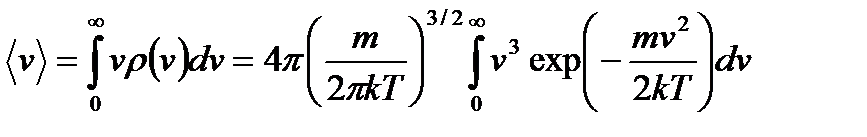 . (2.25)
. (2.25)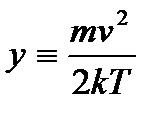 и
и 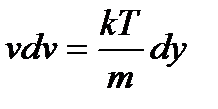 .
.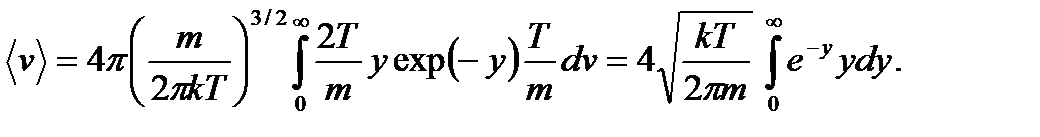
 .
.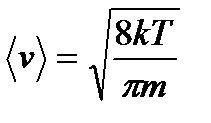 ; (2.26)
; (2.26)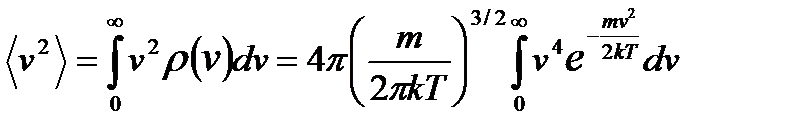 (2.27)
(2.27)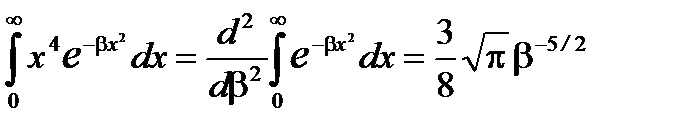
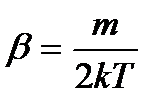 ,
, (2.28)
(2.28)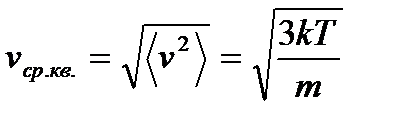 . (2.29)
. (2.29)
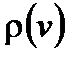 все характерные скорости расположены следующим образом:
все характерные скорости расположены следующим образом: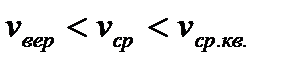 .
.
 (2.31)
(2.31)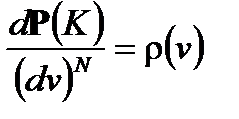 . При больших скоростях эта вероятность быстро спадает
. При больших скоростях эта вероятность быстро спадает 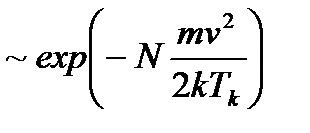 , а при малых ведет себя как
, а при малых ведет себя как  , таким образом в распределении получаем резкий максимум.
, таким образом в распределении получаем резкий максимум.



