
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конденсация Бозе - Эйнштейна.Содержание книги Поиск на нашем сайте
Особый интерес представляет собой случай низких температур. При понижении температуры параметр
Вблизи этой температуры заменять суммирование (3.15) интегрированием нельзя, так как низшие дискретны уровни вносят заметный вклад в сумму. Рассмотрим Пусть
Если теперь взять Отсюда следует, что
При низких температурах T химический потенциал Тогда для T < Tc:
Для T > Tc внутренняя энергия имеет вид
§3.3. Идеальный газ Ферми - Дирака. Для идеального газа фермионов (электронов) свободная энергия также определяется формулой (3.15), в которой числа заполнения
Последнее выражение называется функцией распределения Ферми-Дирака, которая описывает распределение фермионов по энергиям. Для вычисления свободной энергии снова перейдем от суммирования к интегрированию и учтём, что для электронов s =2:
Рассмотрим некоторые свойства функции распределения Ферми-Дирака.
Рис.3.1. Заполнение состояний идеального ферми-газа при Т = 0 и при Т > 0. Из (3.25) следует, что при Т = 0 все состояния с энергиями Так как свободные электроны занимают в импульсном пространстве сферу радиуса p 0, то
Величина
называется энергией (уровнем) Ферми, а Найдем теперь плотность электронных состояний
Полная энергия на единицу объёма при T=0 определяется выражением
Для Т ≠ 0 функцияраспределения расплывается (см. Рис.3.1.), а плотность и внутреннюю энергию можно вычислить лишь приближенно. Энергетический интервал расплывания функции распределения порядка kT, что много меньше значения уровня Ферми
Отсюда следует линейная зависимость удельной теплоемкости металлов от температуры
§3.4. Статистический оператор (матрица плотности) и корреляционные функции. Известно, что в квантовой механике каждой физической величине A соответствует оператор
где
В (3.34) индекс n нумерует состояния, В квантовой статистической механике под наблюдаемой величиной понимается её среднее статистическое значение, которое определяется выражением
В этом выражении
которое означает, что полная вероятность всех вантовых состояний равна единице. Введем квантово-статистический оператор (матрицу плотности), который в матричном представлении (x - представлении) имеет вид
Из ортонормированности волновых функций и (3.37) следует, что
Запишем теперь выражение для среднего значения оператора матрицы плотности (3.37):
=
Здесь мы ввели матричное x - представление для оператора
где шпур берется по координатам x. Последняя запись удобна тем, что она не зависит от представления операторов
В квантовой статистике это представление (n -представление) наиболее удобно. Распределение вероятностей
Поэтому, в x – представлении статистический оператор в случае статистического равновесия даётся выражением
а сам оператор
Независимыми переменными в каноническом ансамбле Гиббса являются температура T, объём V и число частиц N. Поэтому, при суммировании по квантовым состояниям необходимо учитывать только состояния с заданным числом N, что существенно затрудняет процедуру взятия шпура. Чтобы не связывать себя условием постоянства числа частиц, удобно перейти к большому каноническому ансамблю, где независимыми переменными являются T, V и химический потенциал
и накладывается дополнительное условие
где
В (3.47) величина Рассмотрим ансамбль систем с гамильтонианом
где
Таким образом, s w:val="28"/></w:rPr><m:t>(x',t)dx'</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> где
и свойство эрмитовости гамильтониана
Это уравнение называется квантовым уравнением Лиувилля. В операторной форме оно имеет вид
При помощи оператора
Эти средние значения определяют корреляцию одной или нескольких физических характеристик системы частиц и называются корреляционными функциями. В квантовой теории особое значение имеет корреляционная функция двух операторов
В случае равновесия
Использование статистического оператора
Литература 1. А.Н. Матвеев, Молекулярная физика, М., Высшая школа, 1981. 2. Д.В. Сивухин, Курс общей физики, том 2 “Термодинамика и молекулярная физика”, М., Наука, 1979. 3. Ландау Л.Д., Лифшиц Е.М., Теоретическая физика, том 5 “ Статистическая физика”, Часть 1, М., Физматлит, 2001. 4. Р. Фейнман, Статистическая механика, М., “Мир”, 1975.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.49.243 (0.01 с.) |

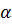 неограниченно возрастает, а дзета- функция при
неограниченно возрастает, а дзета- функция при 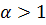 расходится. Температура, при которой
расходится. Температура, при которой 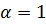 называется критической температурой Tc конденсации Бозе - Эйнштейна. Известно, что
называется критической температурой Tc конденсации Бозе - Эйнштейна. Известно, что 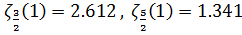 , и из (3.19) находим
, и из (3.19) находим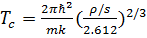 . (3.21)
. (3.21)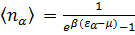 . Так как
. Так как 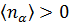 , то должно выполняться условие
, то должно выполняться условие 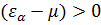 .
.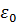 - основное невырожденное состояние, тогда
- основное невырожденное состояние, тогда 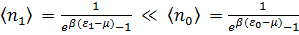 .
.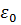 за начало отсчета энергии (
за начало отсчета энергии (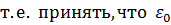 =0), то
=0), то  .
.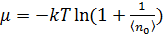 , а для больших
, а для больших 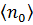
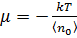 .
.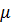 должен лежать вблизи нуля, поэтому для всех энергий
должен лежать вблизи нуля, поэтому для всех энергий  им можно пренебречь.
им можно пренебречь.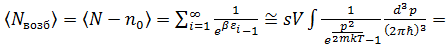
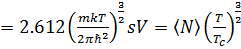 , (3.22)
, (3.22)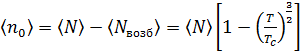 , (3.23)
, (3.23)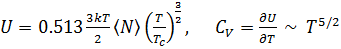 . (3.24)
. (3.24)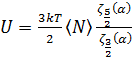 . Эта функция убывает с ростом температуры. Вблизи критической температуры теплоёмкость имеет острый излом (“cusp”).
. Эта функция убывает с ростом температуры. Вблизи критической температуры теплоёмкость имеет острый излом (“cusp”).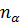 могут принимать всего два значения
могут принимать всего два значения 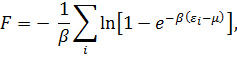
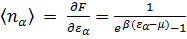 . (3.25)
. (3.25)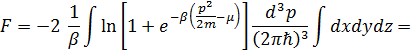
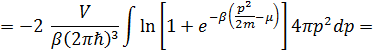
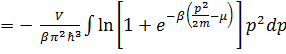 , (3.26)
, (3.26)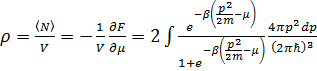 . (3.27)
. (3.27) заполнены, а состояния с большими энергиями
заполнены, а состояния с большими энергиями 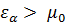 свободны.
свободны.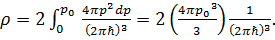 (3.28)
(3.28)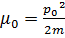 (3.29)
(3.29)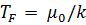 – температурой Ферми. Для простых металлов эту температуру можно оценить, используя две последние формулы -
– температурой Ферми. Для простых металлов эту температуру можно оценить, используя две последние формулы - 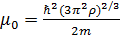 . Оказалось, что, например, для меди (и других металлов в твердом состоянии)
. Оказалось, что, например, для меди (и других металлов в твердом состоянии) 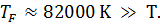 Говорят, что мы имеем сильно вырожденный электронный газ.
Говорят, что мы имеем сильно вырожденный электронный газ.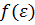 , т.е. число состояний с энергией
, т.е. число состояний с энергией 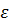 в интервале
в интервале 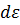 . Этому интервалу в импульсном пространстве отвечает сферический слой толщиной dp. Полное число состояний в данном слое
. Этому интервалу в импульсном пространстве отвечает сферический слой толщиной dp. Полное число состояний в данном слое 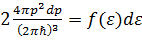 . Отсюда для квадратичного закона дисперсии
. Отсюда для квадратичного закона дисперсии 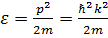 получаем
получаем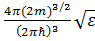 . (3.30)
. (3.30)
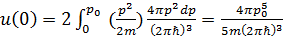 , а средняя энергия электрона в металле равна
, а средняя энергия электрона в металле равна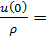
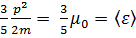 . (3.31)
. (3.31)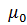 . В результате для низких температур имеем:
. В результате для низких температур имеем: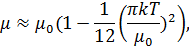
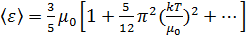 ,
,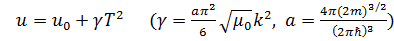 . (3.32)
. (3.32)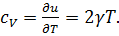
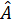 . Наблюдаемыми на опыте значениями этой величины являются квантово - механические средние
. Наблюдаемыми на опыте значениями этой величины являются квантово - механические средние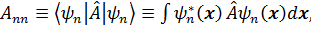 (3.33)
(3.33)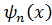 – ортонормированные собственные функции гамильтониана системы:
– ортонормированные собственные функции гамильтониана системы: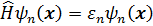 . (3.34)
. (3.34)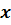 - совокупность независимых координат,
- совокупность независимых координат, 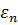 - соответствующие собственные значения. Если оператор
- соответствующие собственные значения. Если оператор 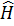 , то система
, то система 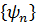 является системой его собственных функций, а наблюдаемые значения (3.33) будут собственными значениями оператора
является системой его собственных функций, а наблюдаемые значения (3.33) будут собственными значениями оператора 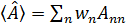 . (3.35)
. (3.35)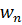 - вероятность обнаружить систему в состоянии n, или статистический вес этого состояния. Очевидно, что должно выполняться условие
- вероятность обнаружить систему в состоянии n, или статистический вес этого состояния. Очевидно, что должно выполняться условие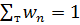 , (3.36)
, (3.36)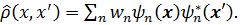 (3.37)
(3.37)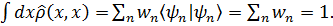 (3.38)
(3.38)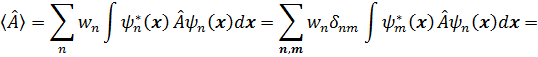
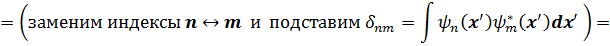
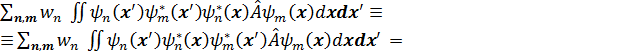
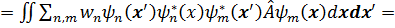
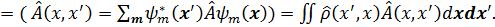 (3.39)
(3.39)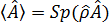 , (3.40)
, (3.40)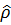 . В частности, под шпуром можно понимать сумму по собственным состояниям
. В частности, под шпуром можно понимать сумму по собственным состояниям (3.41)
(3.41)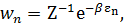 (3.42)
(3.42)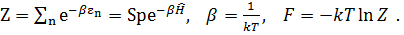 (3.43)
(3.43)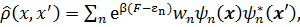 (3.44)
(3.44)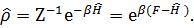 (3.45)
(3.45)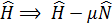 , (3.46)
, (3.46)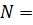 t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>N</m:t></m:r></m:e></m:acc></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>N</m:t></m:r></m:e></m:acc></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 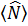 , из которого определятся химический потенциал
, из которого определятся химический потенциал 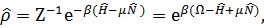 (3.47)
(3.47)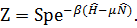 (3.48)
(3.48)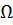 называется термодинамическим потенциалом системы в переменных T, V и
называется термодинамическим потенциалом системы в переменных T, V и 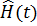 , зависящим от времени. Матрица плотности в этом случае определяется выражением
, зависящим от времени. Матрица плотности в этом случае определяется выражением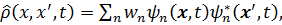 (3.49)
(3.49)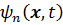 являются решениями нестационарного уравнения Шредингера, удовлетворяющими начальному условию
являются решениями нестационарного уравнения Шредингера, удовлетворяющими начальному условию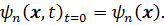 (3.50)
(3.50)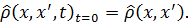 Используя уравнение Шредингера в матричном виде
Используя уравнение Шредингера в матричном виде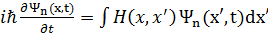 , (3.51)
, (3.51)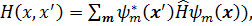 (3.52)
(3.52)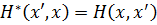 , можно получить уравнение движения статистического оператора в матричной форме
, можно получить уравнение движения статистического оператора в матричной форме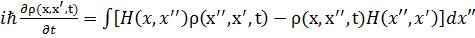 . (3.53)
. (3.53)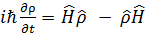 . (3.53)
. (3.53)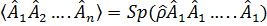 . (3.54)
. (3.54)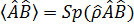 .
.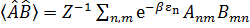 . (3.55)
. (3.55)


