
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. 1. 7 статистическое РаспределениеСодержание книги
Поиск на нашем сайте
1. Закон Максвелла о распределении молекул идеального газа по скоростям и энергиям Важным является распределение числа молекул по скоростям. Движение молекул газа подчиняется законам статистической физики. В среднем скорости и энергии всех молекул одинаковы. Однако в каждый момент времени энергии и скорости отдельных молекул могут значительно отличаться от среднего значения. Статистические методы позволяют найти функцию распределения молекул по скоростям, а также распределение числа молекул по кинетическим энергиям их беспорядочного теплового движения. Впервые это сделал К. Максвелл (1831 – 1879 г.г.), поэтому найденные им выражения называют функциями распределения Максвелла. Приведём наиболее употребительную форму записи закона распределения молекул газа по скоростям (функцию распределения Максвелла)
где График функции (I.28) приведён на рис. 4. Вертикальными линиями отмечены три характерные скорости: наиболее вероятная
При возрастании Относительное число молекул
Наиболее вероятная скорость – скорость, при которой функция распределения молекул идеального газа по скоростям максимальна.Значение её определяется по формуле
Из формулы (I.30) следует, что при повышении температуры максимум функции распределения молекул по скоростям (рис.5) сместится вправо (значение наиболее вероятной скорости становится больше).
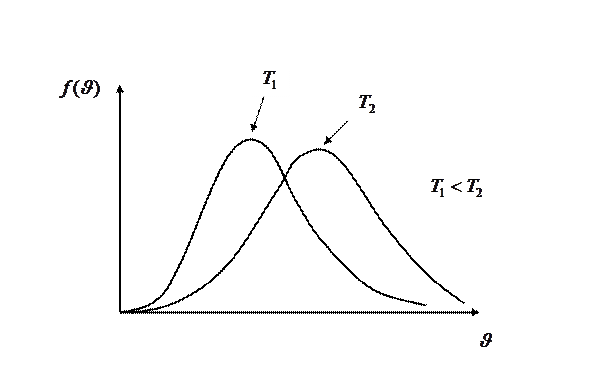
Площадь, ограниченная кривой, остаётся неизменной, в обоих случаях она равна единице. Поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться, что и видно на рис. 5.
Средняя скорость молекулы (средняя арифметическая скорость) определяется по формуле
Согласно формулам (I.24), (I.30) и (I.31)
Таким образом, средняя и средняя квадратичная скорости превышают наиболее вероятную скорость на 13 и 22% соответственно. От распределения по скоростям можно перейти к распределению молекул по значениям кинетической энергии поступательного движения. Эта энергия
Распределение молекул по значениям кинетической энергии поступательного движения имеет вид
где Из (I.34) следует, что функция распределения молекул по значениям
где
2. Распределение частиц в потенциальном силовом поле (распределение Больцмана)
Если молекулы газа движутся в силовом поле (например, в поле тяготения Земли), то, преодолевая действие силы (за счет кинетической энергии), молекула приобретает в данном поле запас потенциальной энергии. Концентрация молекул ( Для изотермической атмосферы распределение молекул по высоте будет иметь вид
Из уравнения (I.36) следует, что с понижением температуры плотность молекул на высотах, отличных от нуля, убывает, обращаясь в нуль при – притяжение молекул к Земле (характеризуемое силой – тепловое движение (характеризуемое энергией
При каждом конкретном распределении молекул по высоте (при каждом значении Выражение
где Л. Больцман доказал, что формула (I.37) справедлива в случае потенциального силового поля любой природы для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения. В связи с этим функцию (I.37) называют распределением Больцмана. Таким образом, распределение (I.36) представляет собой частный случай более общего распределения (I.37). Так как концентрация газа
где Уравнение (I.38) называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты или, измерив давление, найти высоту. Прибор для определения высоты над земной поверхностью называется высотомером (или альтиметром). Его работа основана на использовании формулы (I.38). Из этой формулы следует, что давление с высотой убывает тем быстрее, чем тяжелее газ.
|
||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.237.203 (0.008 с.) |

 , (I.28)
, (I.28) =
= 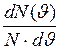 – функция распределения, означающая относительное число молекул, скорости которых лежат в единичном интервале скоростей. Под знаком экспоненты в формуле (I.28) стоит отношение кинетической энергии молекулы (отвечающей данному значению скорости
– функция распределения, означающая относительное число молекул, скорости которых лежат в единичном интервале скоростей. Под знаком экспоненты в формуле (I.28) стоит отношение кинетической энергии молекулы (отвечающей данному значению скорости  ) к величине
) к величине  , характеризующей среднее (по молекулам) значение этой энергии.
, характеризующей среднее (по молекулам) значение этой энергии. , средняя
, средняя  и средняя квадратичная
и средняя квадратичная 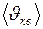 .
.
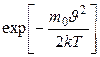 уменьшается быстрее, чем растёт множитель
уменьшается быстрее, чем растёт множитель  и поэтому функция
и поэтому функция  , скорости которых лежат в интервале от
, скорости которых лежат в интервале от  , находится как площадь
, находится как площадь  заштрихованной полоски на рис.4. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция
заштрихованной полоски на рис.4. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция 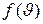 удовлетворяет условию нормировки
удовлетворяет условию нормировки . (I.29)
. (I.29)
 . (I.30)
. (I.30) . (I.31)
. (I.31) . (I.32)
. (I.32) связана со скоростью
связана со скоростью  . (I.33)
. (I.33) , (I.34)
, (I.34) - число молекул, кинетическая энергия поступательного движения которых заключена в пределах от
- число молекул, кинетическая энергия поступательного движения которых заключена в пределах от  .
.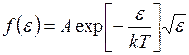 , (I.35)
, (I.35) – нормировочный множитель, равный
– нормировочный множитель, равный  .
.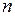 ), находящихся на высоте
), находящихся на высоте 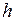 от уровня отсчета и, следовательно, обладающих большим запасом потенциальной энергии, будет отличаться от концентрации молекул (
от уровня отсчета и, следовательно, обладающих большим запасом потенциальной энергии, будет отличаться от концентрации молекул ( ), находящихся на нулевом уровне.
), находящихся на нулевом уровне. . (I.36)
. (I.36)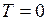 . Это означает, что при абсолютном нуле все молекулы расположились бы на поверхности Земли. С повышением температуры зависимость концентрации от высоты становится всё более слабой, так что молекулы оказываются распределёнными по высоте почти равномерно. Такое поведение функции при изменении температуры объясняется тем, что она отражает «противоборство» двух тенденций:
. Это означает, что при абсолютном нуле все молекулы расположились бы на поверхности Земли. С повышением температуры зависимость концентрации от высоты становится всё более слабой, так что молекулы оказываются распределёнными по высоте почти равномерно. Такое поведение функции при изменении температуры объясняется тем, что она отражает «противоборство» двух тенденций: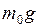 ) стремится расположить их на земной поверхности;
) стремится расположить их на земной поверхности;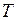 ) обе тенденции уравновешивают друг друга.
) обе тенденции уравновешивают друг друга.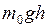 представляет собой потенциальную энергию молекулы
представляет собой потенциальную энергию молекулы  . Поэтому формулу (I.36) можно записать следующим образом
. Поэтому формулу (I.36) можно записать следующим образом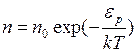 , (I.37)
, (I.37)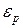 принята равной нулю,
принята равной нулю,  пропорциональна его давлению, то формула связи концентраций молекул
пропорциональна его давлению, то формула связи концентраций молекул 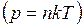 , легко преобразуется в барометрическую, выражающую зависимость давления воздуха
, легко преобразуется в барометрическую, выражающую зависимость давления воздуха 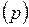 от высоты
от высоты  при постоянной температуре
при постоянной температуре , (I.38)
, (I.38)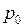 – давление на высоте
– давление на высоте 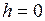 ;
;  – давление на высоте
– давление на высоте 


