
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. 1. 5 закон Авогадро. Закон ДальтонаСодержание книги
Поиск на нашем сайте
Закон Авогадро: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. При нормальных условиях (
Закон Дальтона (давление смеси газов): если в сосуде находится смесь нескольких газов, не вступающих друг с другом в химические реакции, то давление смеси газов равно сумме давлений, производимых каждым газом в отдельности, если бы он один занимал весь сосуд (парциальные давления)
где
I.1.6 ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ. ЗАКОН РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ПО СТЕПЕНЯМ СВОБОДЫ Кинетическая теория газов представляет собой учение о строении и физических свойствах газов, основанное на статистическом методе исследования. Основное уравнение кинетической теории газов устанавливает зависимость между давлением газа
Суммарная кинетическая энергия поступательного движения N молекул газа, находящихся в сосуде, равна
Для однородного газа
Введём среднюю квадратичную скорость
где
Выразим
Подставив уравнения (I.20) и (I.21), в уравнение (I.16) и учитывая, что в 3-х мерном пространстве давление на стенку сосуда осуществляется лишь скоростями или проекциями скоростей в одном направлении, перпендикулярном стенке, получим основное уравнение молекулярно-кинетической теории идеальных газов
где m0 – масса одной молекулы. Средняя квадратичная скорость движения молекул может быть определена по температуре газа. Сравнивая (1.22) с выражением (1.13) и (1.14) и учитывая (1.21),
где Средняя кинетическая энергия поступательного движения молекулы идеального газа
Таким образом, термодинамическая температура есть величина, пропорциональная средней энергии поступательного движения молекул. Заметим, что лишь одноатомные молекулы имеют только поступательное движение, а уравнение (1.24) как раз и описывает этот случай. Двух – и многоатомные молекулы, кроме поступательного, могут совершать также вращательное и колебательное движения. Эти виды движения связаны с некоторым запасом энергии, вычислить который позволяет устанавливаемый классической статистической физикой закон равномерного распределения энергии по степеням свободы. Числом степеней свободы тела называется наименьшее число координат (число независимых координат), которые нужно задать для того, чтобы полностью определить положение тела в пространстве. Закон равномерного распределения энергии по степеням свободы: на каждую степень свободы молекулы в среднем приходится одинаковая кинетическая энергия, равная Из данного закона вытекает, что средняя энергия молекулы определяется по формуле
где
Закон равномерного распределения энергии по степеням свободы приводит к выводу о равноправности всех степеней свободы молекулы – все они вносят одинаковый вклад в её среднюю энергию. Этот вывод имеет ограниченную область применимости и пересмотрен в квантовой статистике. Исключение: СО2 имеет столько же степеней свободы, как и двухатомный газ, т.к. имеет линейную структуру. Ниже приведена таблица 1, по определению числа степеней свободы.
Таблица 1 – Число степеней свободы
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 137; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.186.26 (0.006 с.) |

 ,
, 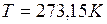 );
); . Д. И. Менделеев закон Авогадро объединил с уравнением Клайперона, отнесенным к одному молю, что и позволило ввести универсальную газовую постоянную R.
. Д. И. Менделеев закон Авогадро объединил с уравнением Клайперона, отнесенным к одному молю, что и позволило ввести универсальную газовую постоянную R. , (I.15)
, (I.15)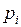 – парциальные давления компонент смеси.
– парциальные давления компонент смеси. , его объёмом
, его объёмом 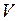 и кинетической энергией поступательного движения его молекул
и кинетической энергией поступательного движения его молекул 
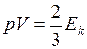 , (I.16)
, (I.16) . (I.17)
. (I.17) 0 (массы всех молекул одинаковы), но скорости
0 (массы всех молекул одинаковы), но скорости 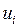 различны и
различны и . (I.18)
. (I.18)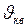 поступательного движения молекул газа
поступательного движения молекул газа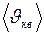
 , (I.19)
, (I.19) – общее число молекул в объёме
– общее число молекул в объёме 
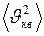 (I.20)
(I.20)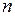 газа
газа . (I.21)
. (I.21) , (I.22)
, (I.22)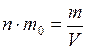 и
и  , получим
, получим ; (I.23)
; (I.23) , (I.24)
, (I.24)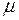 – молярная масса газа, её можно определить по таблице Д.И. Менделеева, или вычислить по формуле
– молярная масса газа, её можно определить по таблице Д.И. Менделеева, или вычислить по формуле  ;
; 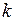 - постоянная Больцмана.
- постоянная Больцмана. . (I.25)
. (I.25)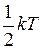 .
.
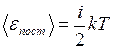 ,(I.26)
,(I.26)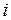 – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы
– сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы . (I.27)
. (I.27)


