
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
II. 1. 3 статистическая физикаСодержание книги
Поиск на нашем сайте
Число молекул, относительные скорости которых заключены в данном интервале (распределение Максвелла )
Относительная скорость молекул
Формула изменения концентрации молекул с высотой
Барометрическая формула
где
Средняя квадратичная скорость молекул
Средняя арифметическая скорость молекул
Наиболее вероятная скорость
где
ЗАДАЧА № II.33 В законе распределения Максвелла для газовых молекул по скоростям кривая распределения асимптотически приближается к оси скоростей. Означает ли это, что молекулы газа, пусть с малой вероятностью, но могут иметь сколь угодно большие скорости? Ответ: Скорость молекул ограничена определенным значением энергии теплового движения газа при данной температуре.
ЗАДАЧА № II.34 Возможны ли в газе с температурой Ответ: Их вероятность исчезающее мала, т.к. кривая распределения Максвелла проходит через начало координат.
ЗАДАЧА № II. 35 Какой вид приобретет барометрическая формула на большой высоте? Ответ: С высотой ускорение свободного падения уменьшается, поэтому необходимо использовать потенциальную энергию гравитационного поля
ЗАДАЧА № II.36 Как можно трактовать нормировку функции распределения Максвелла, а именно Ответ: Как достоверное событие, имеющее вероятность равную единице.
ЗАДАЧА №II.37 Почему отличаются по своему значению средняя квадратичная, средняя арифметическая и наиболее вероятная скорости газовых молекул? Ответ: Это вызвано асимметричностью кривой распределения Максвелла.
ЗАДАЧА№ II.38 Почему с повышением температуры газа вместе с расширением кривой распределения понижается ее максимум? Ответ: Это следует из условия нормировки, а следовательно из постоянства площади под кривой.
ЗАДАЧА № II.39 Влияют ли на максвелловское распределение молекул по скоростям параметры состояния газа? Ответ: Влияет только температура.
ЗАДАЧА № II.40 Если число молекул в сосуде увеличили, не изменив температуры, то как изменится число молекул, обладающих наиболее вероятной скоростью в максвелловском распределении молекул по скоростям? Ответ: Число молекул, обладающих наиболее вероятными скоростями, увеличится.
ЗАДАЧА № II.41 В трех одинаковых сосудах при равных условиях находится одинаковое количество азота (N2), гелия (He), и водорода (H2). На рис. 27 дано распределение скоростей этих молекул. Каким кривым распределения соответствуют молекулы водорода и азота?
Рисунок 27- Распределение скоростей Рисунок 28- Кривые 1 и 2 молекул Ответ: Водороду – 3, азоту – 1. Наиболее вероятная скорость
ЗАДАЧА № II.42 В сосуде, разделенном на равные части неподвижной непроницаемой перегородкой, находится газ. Температуры газа в каждой части сосуда равны, масса газа в левой части больше, чем в правой Ответ: Газ в обеих частях сосуда одинаковый, температуры равны, следовательно наиболее вероятные скорости молекул тоже равны
ЗАДАЧА № II.43 Определить долю молекул водорода, модули скоростей которых при температуре 27° С лежат в интервале от 1898 м/с до 1902 м/с. Дано:
Найти:
Решение В данной задаче удобнее воспользоваться распределением молекул по относительным скоростям. Доля молекул
где С учетом этих выражений формула (1) примет вид
Для удобства сначала вычислим
и отношение скоростей
Подставим численные значения в (1) и найдем долю молекул водорода, модули скоростей которых лежат в интервале от
ЗАДАЧА № II.44 Броуновские частицы с массой 4 фгведут себя в тепловом движении подобно гигантским молекулам, и к ним можно применить закономерности молекулярно-кинетической теории. Исходя из этого, определить, во сколько раз уменьшится концентрация броуновских частиц при увеличении высоты на 1 мм. Температуру принять равной 300 К. Дано:
Найти: Решение Для броуновских частиц воспользуемся распределением молекул по высоте (распределение Больцмана)
где
Прологарифмируем и подставим численные значения,
ЗАДАЧА № II.45 На какой высоте над уровнем моря атмосферное давление составляет 78 кПа, если температура воздуха 170С и не меняется с высотой, а давление на уровне моря нормальное? Найти число частиц в единице объема на этой высоте. Дано:
Найти:
Решение
Если температура не меняется с высотой, то для нахождения давления можно воспользоваться барометрической формулой (II.13)
логарифмируя эту формулу, получаем
Отсюда находим
ЗАДАЧА № II.46 Найти число молекул водорода, заключенных в 1см3 при нормальных условиях, а также число молекул значения скоростей которых лежат в интервале между 399 и 401 м/с. Дано:
Найти: Решение
Число молекул можно найти из распределения Максвелла, заданного в виде уравнения (II.10)
Для всех газов при нормальных условиях число молекул в 1 см3 одно и то же и равно Вычислим значения величин, входящих в распределение Максвелла
ЗАДАЧА № II.47 Температура окиси азота (NO) 300 К. Определить долю молекул, скорость которых лежит в интервале от 820 м/с до 830 м/с.
Дано:
Найти:
Решение Рассматриваемый газ находится в равновесном состоянии. Согласно распределению Максвелла, относительное число молекул, скорость которых заключена в интервале от где
Тогда
Аналогично подсчитаем В условии задачи требуется определить долю молекул, скорости которых лежат в диапазоне Если в этом пределе функцию Максвелла можно с достаточной степенью точности считать постоянной, то искомая величина может быть рассчитана по приближённой формуле
Следовательно, с указанной степенью точности можно использовать равенство II.1.4 ФИЗИЧЕСКАЯ КИНЕТИКА Средняя длина свободного пробега молекул газа
где
Среднее число столкновений одной молекулы в единицу времени
Общее число столкновений всех молекул в единице объема за единицу времени
Число молекул, ударяющихся за единицу времени в единичную площадку, которая помещена в газе
Закон диффузии (закон Фика): масса определенного компонента газа(
где
Знак минус обусловлен тем, что перенос массы происходит в направлении убывания плотности. Коэффициент диффузии
Закон теплопроводности (закон Фурье): количество теплоты (
где
Знак минус означает, что перенос внутренней энергии происходит в направлении убывания температуры. Коэффициент теплопроводности
где Закон вязкости (закон Ньютона): сила внутреннего трения (
где
Знак минус означает, что сила трения, действующая на более быстро движущиеся слои, направлена против скорости. Коэффициент динамической вязкости
ЗАДАЧА № II.48 Чем объяснить, что при высокой средней скорости хаотического движения газовых молекул (для воздуха Ответ:При обычном давлении длина свободного пробега молекул газа мала и энергия теплового движения передается молекулами от слоя к слою через очень большое число столкновений, что и замедляет передачу тепла. ЗАДАЧА № II.49 Для чего в сосуде Дьюара создают вакуум? Ответ:В плотном газе теплопроводность не зависит от давления. Когда создается вакуум (ультраразряженный газ) толщина слоя воздуха между стенками сосуда оказывается равна или меньше длины свободного пробега, и молекулы между собой не сталкиваются. В этом случае теплопроводность пропорциональна концентрации молекул, а, следовательно, и давлению газа. Чем разряженнее воздух, тем меньше теплопроводность. ЗАДАЧА № II.50 Коэффициенты теплопроводности газов имеют следующие значения Водород 4,2 ·106 Вт / м·град Гелий 3,4 ·106 Вт / м·град Кислород 0,57 ·106 Вт / м·град Углекислый газ 0,34 ·106 Вт / м·град Какой газ выгоднее использовать для охлаждения? Какой для теплоизоляции? Ответ:Для охлаждения выгоднее использовать водород (быстрее забирает тепло), для теплоизоляции – углекислый газ (медленнее уходит тепло).
ЗАДАЧА № II.51 Почему при резком движении в неподвижном воздухе чувствуется ветер? Ответ:Ощущение ветра возникает в результате действия силы трения из-за появления градиента скоростей в прилегающем воздухе.
ЗАДАЧА № II.52 Почему в закрытом помещении возникший снаружи резкий запах начинает чувствоваться? Ответ:Вматериале стен и окон имеются узкие щели и поры, через которые в результате диффузии молекулы вещества, вызвавшего запах, проникают в помещение.
ЗАДАЧА № II.53 Почему в горячей воде сахар растворяется быстрее, чем в холодной? Ответ: С увеличение температуры возрастает скорость хаотического движения, а следовательно увеличивается скорость диффузии молекул сахара.
ЗАДАЧА № II.54 Как изменится эффективный диаметр молекул газа при изохорическом увеличении давления? Ответ: Уменьшится, т.к. он убывает с ростом температуры.
ЗАДАЧА № II.55 Какое явление имеет место при наличии градиента скорости слоев жидкости или газа? Ответ: Явление внутреннего трения.
ЗАДАЧА № II.56 В потоке жидкости, направленном вдоль оси х, скорость жидкости растет в положительном направлении оси у. В каком направлении происходит перенос импульса направленного движения? Ответ: В отрицательном направлении оси
ЗАДАЧА № II.57 Стальной стержень длиной 40 см и площадью поперечного сечения 6 см2 нагревается так, что с одного конца его температура поддерживается 3500С, а с другого находится лед при 00С. Считая, что передача теплоты осуществляется лишь вдоль стержня, подсчитать массу льда, растаявшего за 6 мин. Коэффициент теплопроводности стали 67,2 Дж/(град·м·с). Дано:
Найти: Решение
Количество теплоты, переданной через какое либо сечение стержня от нагретого конца к холодному за время t, определяется на основании закона Фурье (II.23). Для нашего случая этот закон можно представить в виде
где Лед у холодного конца плавится. На плавление данной массы льда тратится энергия
где Так как
Подстановка численных значений дает ЗАДАЧА № II.58 Рассчитать среднюю длину свободного пробега молекул азота, коэффициент диффузии и вязкость при давлении 10 5 Па и температуре 17 0С. Как изменятся найденные величины в результате двукратного увеличения объёма газа: а) при постоянном давлении; б) при постоянной температуре? Эффективный диаметр молекул азота 3,7·10 –8 см.
Дано:
Найти:
Решение
Средняя длина свободного пробега может быть рассчитана по формуле
где Для расчёта коэффициента диффузии по формуле:
рассчитаем по формуле
Как видно из формулы, средняя длина свободного пробега зависит только от концентрации молекул. При двукратном увеличении объёма концентрация уменьшается вдвое. Следовательно, при любом процессе В выражение коэффициента диффузии входит не только длина свободного пробега, но и средняя скорость. Следовательно,
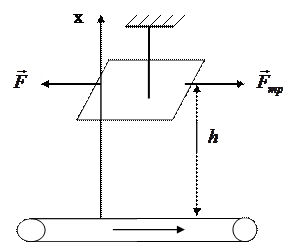
При постоянном давлении объём прямо пропорционален термодинамической температуре: температуры, т.е. ЗАДАЧА № II.59 На высоте 20 см над горизонтальной трансмиссионной лентой, движущейся со скоростью 70 м/с, параллельно ей подвешена пластинка площадью 4 см2. Какую силу надо приложить к этой пластинке, чтобы она оставалась неподвижной? Вязкость воздуха при нормальных условиях 1,7·10 – 5 кг/(м·с). В условиях опыта температура 27 0С, давление атмосферное (рис. 29).
Дано:
Найти: Решение
Благодаря явлению внутреннего трения на слой воздуха, примыкающий к пластинке (адсорбированный пластинкой), действует со стороны движущихся слоёв сила трения. Пластинка будет неподвижна, если приложенная сила F и сила трения F тр скомпенсированы F = – F тр, или в скалярном виде
h
Рисунок 29 - Рисунок к задаче № II.59
Сила трения может быть найдена из закона Ньютона где По условию задачи, давление атмосферное, это значит, что длина свободного пробега молекул много меньше расстояния h, поэтому вязкость может быть рассчитана по формуле
Здесь
Как видно, вязкость зависит только от природы газа (эффективного диаметра молекул
Из закона сохранения импульса следует, что сила трения, действующая на любой из этих промежуточных слоёв, должна быть одинаковой, следовательно,
§II.2.1 ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ Первое начало термодинамики имеет вид
где
Изменение внутренней энергии идеального газа
где Связь между молярной и удельной теплоемкостями
где Теплоемкость газа при постоянном объеме
где
Теплоемкость газа при постоянном давлении (уравнение Майера)
Работа при изотермическом процессе
Работа при изобарическом процессе
Работа при адиабатическом процессе
где Уравнения Пуассона
ЗАДАЧА № II.60 Можно ли говорить о количестветепла, содержащемся в теле? Ответ: нельзя, так как количество тепла не является функцией состояния системы, а характеризует процесс теплопередачи и зависит от способа теплопередачи.
ЗАДАЧА № II.61 Почему наличие большого водоема смягчает климат? Ответ: Водоем обладает большой теплоемкостью. При похолодании, когда температура воздуха меньше температуры воды, вода отдает большее количества тепла. При потеплении, когда температура воздуха выше температуры воды, вода поглощает много тепла. Этим объясняется сглаживание температурных контрастов.
ЗАДАЧА № II.62 Почему при холостых выстрелах ствол пушки нагревается сильнее, чем при стрельбе снарядами? Ответ: Энергия, выделяемая при сгорании пороха, в случае холостого выстрела вся идет на нагревание ствола, а при стрельбе снарядами часть энергии идет на придание кинетической энергии снаряду и отдачи.
ЗАДАЧА № II.63 Послесильногоштормаводавморе становится теплее. Почему? Ответ: Нагревание воды происходит за счет превращения механической энергии волн при трении одних слоев о другие в тепло.
ЗАДАЧА № II.64 Нагретый сжатый идеальный газ с силой вырывается через два одинаковых сопла наружу. Одна из струй попадает на лопасти турбины, приводя ее во вращение. В какой струе газ охлаждается сильнее? Почему? Ответ: В струе, падающей на лопасти турбины, т.к. часть тепла расходуется на работу турбины. ЗАДАЧА № II.65 Идеальный газ совершает цикл, состоящий из двух изотерм и двух изохор (рис.30). Как ведут себя на каждом участке:
выражение внутренней энергии идеального газа
В результате получим: (1–2) – изотермическое расширение при температуре
(2–3) – изохорический процесс с понижением температуры от T1 до T2,
(3–4) – изотермическое сжатие при температуре
(4–1) – изохорический процесс с повышением температуры от ЗАДАЧА № II.66 Идеальныйгазрасширяетсяотобъема а)адиабатически; б)изобарически; в)изотермически. При каком процессе произведена наименьшая работа?
Рисунок 31 – Графики процессов Ответ: При адиабатическом процессе (рис.31). Работа равна
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 177; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.37.242 (0.013 с.) |

 (II.10)
(II.10)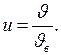 (II.11)
(II.11)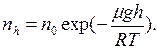 (II.12)
(II.12) (II.13)
(II.13)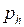 и
и 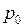 – давление,
– давление,  и
и  – концентрация газа на высоте
– концентрация газа на высоте 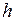 и
и 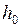 ;
;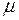 - молярная масса газа;
- молярная масса газа; 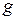 – ускорение свободного падения.
– ускорение свободного падения.
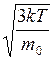 . (II.14)
. (II.14)
 . (II.15)
. (II.15)
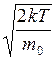 ,(II.16)
,(II.16) – масса одной молекулы.
– масса одной молекулы.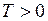 К неподвижные молекулы?
К неподвижные молекулы?
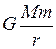 , и барометрическая формула примет вид
, и барометрическая формула примет вид 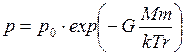 , где
, где 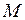 – масса Земли,
– масса Земли,  – масса молекулы газа.
– масса молекулы газа.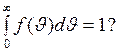

 , она зависит от молярной массы газа и будет наименьшей для азота, (
, она зависит от молярной массы газа и будет наименьшей для азота, ( г/моль) и наибольшей у водорода (
г/моль) и наибольшей у водорода ( г/моль).
г/моль). . Какими кривыми (рис.28) будут описываться функции распределения молекул по скоростям для молекул газа в правой и левой частях сосуда?
. Какими кривыми (рис.28) будут описываться функции распределения молекул по скоростям для молекул газа в правой и левой частях сосуда? . Массы разные
. Массы разные 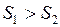 . Кривая 1 – для левой части, кривая 2 – для правой части.
. Кривая 1 – для левой части, кривая 2 – для правой части. кг/моль;
кг/моль;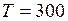 К;
К;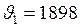 м/с;
м/с;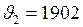 м/с.
м/с.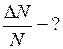
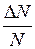 , относительные скорости которых заключены в интервале от
, относительные скорости которых заключены в интервале от  до
до 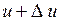 , определяется формулой
, определяется формулой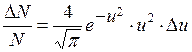 , (1)
, (1)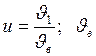 – наиболее вероятная скорость;
– наиболее вероятная скорость;  .
.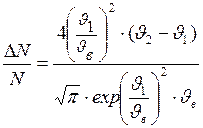 .
.
 (м/с),
(м/с), .
.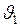 до
до 
 .
.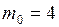 фг
фг 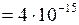 г
г 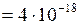 кг;
кг; мм
мм  м;
м;
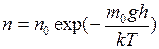 ,
,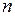 и
и 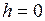 , соответственно. Выразим
, соответственно. Выразим
 .
.
 Итак,
Итак,  то есть концентрация частиц уменьшится в
то есть концентрация частиц уменьшится в 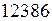 раз.
раз.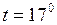 C
C 
 К;
К; Па;
Па; Па;
Па; кг/моль.
кг/моль.
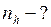
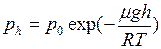

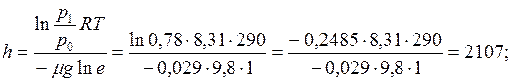


 м;
м; 
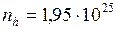 м-3.
м-3. см3
см3  м3;
м3; Па;
Па;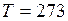 К;
К; м/с;
м/с;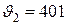 м/с;
м/с;
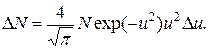
 см-3 (число Лошмидта).
см-3 (число Лошмидта). ,
, 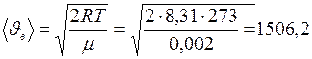 м/с;
м/с;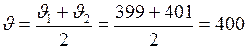 м/с;
м/с; 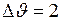 м/с;
м/с;


 м/с;
м/с;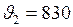 м/с;
м/с; кг/моль.
кг/моль.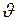 до
до  ,
, 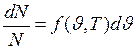 ,
, – функция распределения Максвелла, которую можно представить в виде:
– функция распределения Максвелла, которую можно представить в виде: 
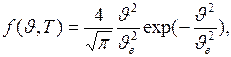 где
где  м/с.
м/с.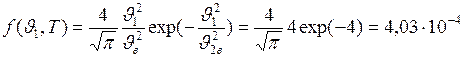 с/м.
с/м. с/м.
с/м. м/с.
м/с. т.е.
т.е. 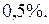 Это значит, что при использовании этой формулы допускается ошибка, относительная величина которой
Это значит, что при использовании этой формулы допускается ошибка, относительная величина которой .
.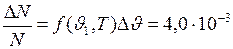 , или
, или 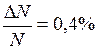 .
. ,(II.17)
,(II.17) – эффективный диаметр молекул;
– эффективный диаметр молекул; . (II.18)
. (II.18)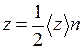 . (II.19)
. (II.19)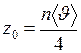 . (II.20)
. (II.20) ), диффундирующая за время (
), диффундирующая за время ( )через площадку (
)через площадку ( ), расположенную перпендикулярно оси х
), расположенную перпендикулярно оси х (II.21)
(II.21)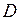 – коэффициент диффузии;
– коэффициент диффузии; − градиент плотности.
− градиент плотности. . (II.22)
. (II.22)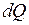 ), переносимое за время (
), переносимое за время (
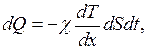 (II.23)
(II.23) − коэффициент теплопроводности;
− коэффициент теплопроводности;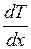 − градиент температуры;
− градиент температуры; - плотность газа.
- плотность газа.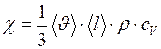 , (II.24)
, (II.24) – удельная теплоемкость газа при постоянном объеме.
– удельная теплоемкость газа при постоянном объеме. ) между двумя слоями площадью (
) между двумя слоями площадью (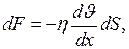 (II.25)
(II.25) - коэффициент динамической вязкости;
- коэффициент динамической вязкости; − градиент скорости течения газа в направлении, перпендикулярном к площадке
− градиент скорости течения газа в направлении, перпендикулярном к площадке 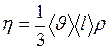 . (II.26)
. (II.26) м/с) возникшая в газе разница температур выравнивается сравнительно медленно (т.е. теплопроводность газов мала).
м/с) возникшая в газе разница температур выравнивается сравнительно медленно (т.е. теплопроводность газов мала). .
.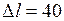 см
см  м;
м; см2
см2  м2;
м2;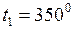 С;
С;  К;
К; С;
С;  K;
K;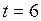 мин
мин  с;
с;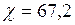 Дж/(град·м·с);
Дж/(град·м·с); Дж/кг.
Дж/кг.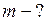
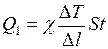 ,
,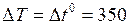 К.
К.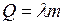 ,
,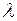 – удельная теплота плавления льда.
– удельная теплота плавления льда. , то для массы льда (
, то для массы льда (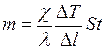 ;
; кг.
кг. см
см  м;
м;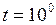 С;
С;  кг/моль
кг/моль
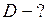
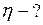
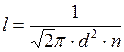 ,
, . Тогда
. Тогда 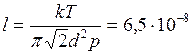 м.
м. , воспользуемся полученным результатом, определив предварительно среднюю скорость
, воспользуемся полученным результатом, определив предварительно среднюю скорость м/с. Тогда
м/с. Тогда 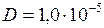 м2/с. Коэффициент вязкости
м2/с. Коэффициент вязкости кг/(м∙с)
кг/(м∙с) . Индексы 1 и 2 соответствуют состояниям до, и после расширения газа.
. Индексы 1 и 2 соответствуют состояниям до, и после расширения газа. .
.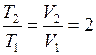 . Таким образом,
. Таким образом,  . Вязкость, зависит только от скорости молекул, следовательно, и от
. Вязкость, зависит только от скорости молекул, следовательно, и от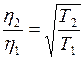 . Это значит, что при постоянном давлении
. Это значит, что при постоянном давлении  . При постоянной температуре коэффициент
. При постоянной температуре коэффициент  не изменяется.
не изменяется. см
см 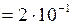 м;
м; м/с;
м/с; см2
см2 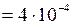 м2;
м2; кг/(м·с);
кг/(м·с); К;
К; 0C;
0C; 
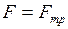 .
.
 ,
, – производная скорости
– производная скорости  направленного движения слоя по координате х, причём ось Ох перпендикулярна плоскостям трансмиссии и пластинки и направлена от трансмиссии к пластинке.
направленного движения слоя по координате х, причём ось Ох перпендикулярна плоскостям трансмиссии и пластинки и направлена от трансмиссии к пластинке. .
. – средняя скорость теплового движения молекул;
– средняя скорость теплового движения молекул;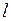 – средняя длина свободного пробега молекул;
– средняя длина свободного пробега молекул;  – плотность газа.
– плотность газа. и значение
и значение  при заданных условиях связано со значением
при заданных условиях связано со значением  при нормальных условиях соотношением
при нормальных условиях соотношением  , отсюда
, отсюда  .
. и значение этой производной может быть определено из граничных условий. Так как
и значение этой производной может быть определено из граничных условий. Так как 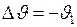 ,
, 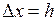 . Тогда
. Тогда  (как и следовало ожидать, производная
(как и следовало ожидать, производная  ). Подставляя значения
). Подставляя значения 
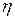 в формулу для силы, получим
в формулу для силы, получим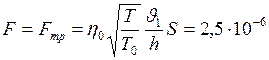 Н.
Н. , (II.27)
, (II.27) – приращение внутренней энергии системы;
– приращение внутренней энергии системы;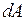 – работа, совершаемая системой против внешних сил.
– работа, совершаемая системой против внешних сил.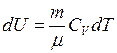 , (II.28)
, (II.28) – молярная теплоемкость газа при постоянном объеме.
– молярная теплоемкость газа при постоянном объеме.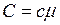 , (II.29)
, (II.29) , (II.30)
, (II.30)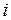 – число степеней свободы движения молекулы.
– число степеней свободы движения молекулы.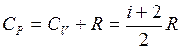 . (II.31)
. (II.31) . (II.32)
. (II.32) . (II.33)
. (II.33) , (II.34)
, (II.34)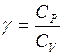 − показатель адиабаты.
− показатель адиабаты. ;
; 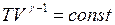 ;
; 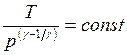 . (II.35)
. (II.35)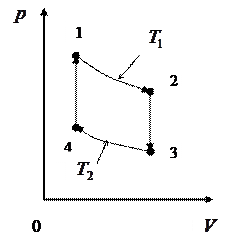
 Рисунок 30- Заданный цикл
Рисунок 30- Заданный цикл

 , работу газа
, работу газа  , условия
, условия  .
. 
 ,
,  ,
, (газ совершает работу путем расширения),
(газ совершает работу путем расширения), 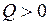 (газ получает тепло от нагревателя);
(газ получает тепло от нагревателя);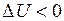 (внутренняя энергия убывает),
(внутренняя энергия убывает), 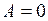 , так как
, так как 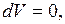
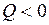 (газ отдает тепло охладителю);
(газ отдает тепло охладителю);

 до
до 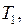
 (внутренняя энергия растет)
(внутренняя энергия растет) 
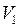 до объема
до объема 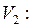

 и численно может быть найдена по площади криволинейной трапеции, ограниченной графиком процесса, ординатами начального и конечного со
и численно может быть найдена по площади криволинейной трапеции, ограниченной графиком процесса, ординатами начального и конечного со 


