
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. 3. 9 тепловые явления в средах при механическом воздействииСодержание книги
Поиск на нашем сайте
Законы термодинамики являются общими для любых макроскопических систем; газов, жидкостей, твердых тел, растворов, сплавов и т.п. Эти законы, в частности, проявляются в виде тепловых эффектов (охлаждении или нагревании) при различных физических воздействиях: механических, электрических, магнитных и т.п. Остановимся на механических воздействиях. В идеальных газах, как указывалось выше, в которых отсутствуют силы притяжения между молекулами и размерами молекул можно пренебречь, при адиабатическом расширении происходит охлаждение газа, а при сжатии – нагревание. В реальных газах, при наличии сил притяжения между молекулами и с учетом размеров молекул, наблюдается при адиабатическом расширении как положительный (охлаждение), так и отрицательный (нагревание) эффект, т.е. так называемый эффект Джоуля-Томсона. Жидкости и твердые тела являются конденсированными средами, в которых частицы вещества плотно прилегают друг к другу. В результате их сжимаемость (и растяжимость) под воздействием механических сил в тысячи раз меньше, чем у газов. Тем не менее, деформации происходят и также сопровождаются тепловыми эффектами, в проявлении которых начинают играть дополнительные факторы. Например, в жидкостях проявляется действие сил поверхностного натяжения. Еще более сложная картина наблюдается в кристаллах, и характер теплового эффекта зависит от многих факторов: направления механического напряжения, вида деформации, особенности химической природы вещества, симметрии кристаллической структуры и др. Но есть и закономерности. Так, большинство кристаллов увеличивает все свои размеры при повышении температуры. Тогда любое растягивающее напряжение приводит к охлаждению теплоизолированного (условие адиабаты) кристалла, а сжимающее – к его нагреванию. Известно, что для длинного тонкого стержня (или проволоки), когда действует растягивающее напряжение вдоль стержня, имеет место удлинение стержня. Удлинение стержня наблюдается также и при нагревании. И согласно законам термодинамики между этими явлениями должна быть связь. Например, если такому телу сообщается некоторое количество теплоты и оно при этом удлиняется, то эта теплота расходуется согласно первому началу термодинамики на нагревание (т.е. на увеличение внутренней энергии) и на работу упругих сил в результате удлинения.
ЧАСТЬ II. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Глава II.1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНЫХ ГАЗОВ §II.1.1 ИДЕАЛЬНЫЕ ГАЗЫ. ГАЗОВЫЕ ЗАКОНЫ . Любой газ можно охарактеризовать его массой Закон Бойля – Мариотта. При
Этот закон описывает изотермический процесс. Закон Гей – Люссака. При
Этот закон описывает изобарический процесс. Закон Шарля. При
Этот закон описывает изохорический процесс. Объединенный закон газового состояния (формула Клапейрона). При
Если по условию задачи газ находится при одних каких-либо условиях, то его сравнивают с состоянием данного газа при нормальных условиях:
Уравнение Клапейрона – Менделеева (универсальное уравнение газового состояния)
где R = 8,31 Дж/(моль·К) – постоянная для всех газов величина, называемая молярной газовой постоянной (или универсальной газовой постоянной). Закон Дальтона. Если в сосуде находится смесь нескольких газов, не вступающих друг с другом в химические реакции, то давление смеси газов равно сумме давлений, производимых каждым газом в отдельности, если бы он один занимал весь сосуд (парциальные давления)
где ЗАДАЧА № II.1 На диаграмме
Ответ: Процесс 1–2 изохорический, так как в нем давление прямо пропорционально температуре; процесс 2–3 – изотермический; процесс 3–1 – изобарический. Данный цикл на
ЗАДАЧА № II.2 При нагревании газа получена зависимость давления от температуры (рис.20). Сжимается или расширяется газ во время нагревания?
Рисунок 20 - Диаграмма
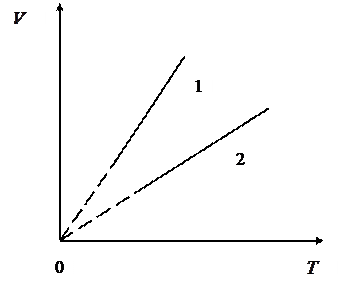
Ответ: Газ расширяется. Если провести изохоры через точки 1 и 2 (рис.21), то легко убедиться, что ЗАДАЧА № II.3 На рис.22 изображены две изобары. Какая из изобар соответствует большей массе газа?
Ответ: Первая, так как при одинаковых давлении и температуре большая масса занимает больший объём.
Рисунок 22 – Две изобары
Ответ: Первая, так как при одинаковых давлении и температуре большая масса занимает больший объём.
ЗАДАЧА № II.4 Под колоколом воздушного насоса стоит банка с водой, в ней пузырек. Как изменяется объем пузырька при откачивании воздуха? Температура постоянная. Ответ: Объем пузырька увеличивается, т.к. по закону Бойля-Мариотта
ЗАДАЧА № II.5 Две колбы с воздухом при нормальном давлении и различные по объему закупоривают и нагревают в парах кипящей воды до 1000 С. Одинаковым ли будет в них давление воздуха после нагревания? Ответ: Давление будет одинаковым, т.к. в обеих колбах плотности воздуха равны и не изменяются при нагревании
ЗАДАЧА № II.6 В газоразрядной плазме (искра, электрическая дуга), состоящей из электронов, ионов, нейтральных атомов и молекул, в разных компонентах разная температура. Почему это возможно? Ответ: При электрическом разряде процессы протекают очень быстро (меньше времени релаксации), поэтому общая температура не успевает установиться.
ЗАДАЧА № II.7 Найти молярную массу воздуха, считая, что он состоит по массе из одной части кислорода и трех частей азота. Дано:
Найти: Решение
Воздух, являясь смесью идеальных газов, тоже представляет идеальный газ, и к нему можно применить уравнение Клапейрона-Менделеева
Для каждой компоненты смеси кислорода и азота запишем соответствующее уравнение:
где По закону Дальтона давление воздуха
Сравнивая (1) и (4) и учитывая, что
Подставляя в (5)
Подставляя численные значения, получим
ЗАДАЧА № II.8 Как изменится давление идеального газа, если его объем и температуру уменьшить в два раза?
Решение
Уравнение Клапейрона – Менделеева приводит к следующему выражению для давления газа
Если объем
ЗАДАЧА № II.9 Объем пузырька воздуха по мере всплывания его со дна озера на поверхность увеличивается в три раза. Какова глубина озера? Дано:
Найти: Решение
Считаем, что температура воды в озере на любой глубине постоянна. Тогда по закону Бойля – Мариотта
где
Очевидно, что давление Следовательно, увеличение давления у дна озера будет
Как известно из гидростатики, где
Приравнивая правые части двух последних уравнений, получим
откуда
ЗАДАЧА № II.10 Сосуд вместимостью 20 л, заполненный воздухом при давлении 0,4 МПа, соединяют с сосудом, из которого воздух удалён. При этом давление в обоих сосудах становится одинаковым и равным 1,0·105 Па. Определить вместимость второго сосуда. Процесс изотермический.
Дано:
Найти: Решение Изотермический процесс протекает при постоянной температуре
дает
ЗАДАЧА № II.11 Изменение состояния идеального газа описывается приведенным графиком (рис.23). Как изменяется температура при переходе газа из состояния 1 в состояние 3?
Рисунок 23 - График зависимости давления от объёма
Решение
При переходе газа из состояния 1 в состояние 2 (
ЗАДАЧА № II.12 При какой температуре находился газ, если в результате изобарного нагревания на 1К его объём увеличился на 3,5·10-3 от первоначального? Дано:
Найти: Решение В результате нагревания температура газа повысилась на 1К, следовательно,
Подстановкой численных значений получим:
ЗАДАЧА № II.13 В баллоне находится идеальный газ. Когда часть газа выпустили, температура газа в баллоне уменьшилась в 3 раза, а давление – в 4 раза. Какую часть газа (в процентах) выпустили?
Дано:
Найти: Решение Для двух описанных ситуаций уравнение состояния имеют вид
и
где
ЗАДАЧА № II.14 На рис.24 показаны две изохоры для газа одной и той же массы. Углы наклона изохор к оси абсцисс равны
Рисунок 24 - График двух изохор для газа одной и той же массы Решение Уравнения состояния позволяют записать для двух разных объёмов взаимосвязь параметров При некоторой температуре из графика (см. рис.24) определим, что
Поделив уравнение (3) на (4), получим искомое соотношение объемов
ЗАДАЧА № II.15 Давление воздуха внутри бутылки, закрытой пробкой равно 0,1 МПа при температуре 7 0С. На сколько градусов нужно нагреть воздух в бутылке, чтобы пробка вылетела? Без нагревания пробку можно вынуть, прикладывая к ней силу 30 Н. Поперечное сечение пробки 2 см2.
Дано:
Найти: Решение
Чтобы пробка вылетела из бутылки, необходимо, чтобы давление воздуха в бутылке равнялось
Для того чтобы пробка вылетела из бутылки, необходимо воздух в ней нагреть на ЗАДАЧА № II.16 Начертите график зависимости плотности газа от температуры при изобарическом процессе и зависимости плотности газа от давления при изотермическом процессе,
Решение Согласно уравнению Клапейрона – Менделеева
Следовательно, зависимость
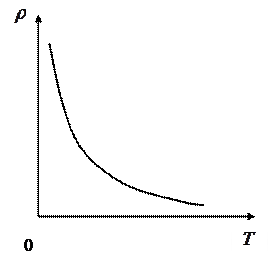
Рисунок 25 - Зависимость плотности Рисунок 26 - Зависимость плотности от температуры от давления
ЗАДАЧА № II.17 Имеется смесь из 4,4·1021 молекул кислорода, 0,9·1021 молекул углекислоты и 2,1·10 21 молекул азота. Найти давление этой смеси на стенки сосуда емкостью 2 л, если сосуд нагрет до 200С, и молекулярную массу смеси.
Дано:
Найти: Решение
Из уравнения Клапейрона - Менделеева
Парциальные давления кислорода, углекислоты и азота равны
где
Давление смеси газов можно рассчитать по закону Дальтона (3)
где
Подстановка численных значений дает
Приравняв правые части уравнений (2) и (4), получим
Массу газа
определим молярную массу смеси
§II.1.2ОСНОВЫ МОЛЕКУЛЯРНО - КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ Все вещества состоят из атомов и молекул. Для измерения количества вещества вводится единица – моль. В моле любого вещества содержится одинаковое число молекул Все молекулы находятся в непрерывном хаотическом движении, которое называется тепловым. Молекулы газа обладают средней кинетической энергией поступательного движения
где
Согласно молекулярно – кинетической теории, эта энергия связана с термодинамической температурой соотношением
где
Зависимость давления газа от концентрации молекул и температуры
ЗАДАЧА № II.18 Какой импульс передает молекула стенке сосуда, если, падая перпендикулярно к стенке: 1) отразится упруго с той же скоростью; 2) прилипнет к стенке? Масса молекулы
Ответ: 1) ЗАДАЧА № II.19 Какие молекулы в атмосфере движутся быстрее: молекулы кислорода или азота? Ответ: Молекулы азота, так как ЗАДАЧА № II.20 Водород и кислород равной массы помещены в цилиндры со свободно перемещающимися поршнями. Чем будут отличаться изобары этих газов? Ответ: Поскольку молекулы водорода и кислорода двухатомные, то при одной и той же температуре их средние кинетические энергии ЗАДАЧА № II.21 Запуск искусственных спутников показал, что температура воздуха на высоте 1000 км достигает нескольких тысяч градусов. Почему же не расплавляется спутник, двигаясь на этой высоте? Температура плавления железа 15200С. Ответ: Из-за большой разреженности воздуха на высоте 1000 км он не может передать спутнику то количество теплоты, которое необходимо для его плавления.
ЗАДАЧА № II.22 Средняя кинетическая энергия молекул газа при температуре Т зависит от их структуры, что связано с возможностью различных видов движения атомов в молекуле. При условии, что имеют место только поступательное и вращательное движение, определить среднюю энергию молекул водяного пара (Н2О ). Ответ: Средняя кинетическая энергия любой молекулы
ЗАДАЧА № II.23 Для молекулы воды (Н2О) имеют место все виды движения. Чему равно число степеней свободы для такой молекулы? Ответ: i = 9 (3 поступательных + 3 вращательных + 3 колебательных).
ЗАДАЧА № II.24 Чему равно число степеней свободы для атомарного водорода? Ответ: i = 3 (поступательных, вращательных и колебательных нет).
ЗАДАЧА № II.25 Сколько молекул содержится в стакане воды? Дано:
Найти:
Решение Учитывая, что в моле находится
ЗАДАЧА № II.26 Плотность некоторого газа равна6·10–2 кг/м3, средняя квадратичная скорость молекул этого газа 500 м/с. Определить давление, которое газ оказывает на стенку сосуда. Дано:
Найти: Решение Восновном уравнении молекулярно-кинетической теории
Произведение
ЗАДАЧА № II.27 Определить среднюю квадратичную скорость молекул кислорода при 200С. При какой температуре эта скорость равна 500 м/с?
Дано:
Найти: Решение Кинетическая энергия одной молекулы газа равна
Согласно молекулярно – кинетической теории, средняя кинетическая энергия поступательного движения одной молекулы газа
Приравнивая правые части данных уравнений, получаем выражение для скорости
Так как
Запишем уравнение для
ЗАДАЧА № II.28 В сосуде емкостью 3,5 л находится смесь газов, в которую входит 2·1015 молекул кислорода, 5·1015 молекул азота и 6,6·10-7г аргона. Какова температура смеси, если давление в сосуде 1,74·10-4 мм.рт.ст.? Дано:
Найти:
Решение Для нахождения температуры смеси можно использовать зависимость давления газа от концентрации молекул и температуры
На основании закона Дальтона
где Для аргона
Отсюда искомая температура
Подставляя численные значения и проведя расчет, получим
ЗАДАЧА № II.29 Оцените число молекул воздуха, падающих на 1 см2 стены комнаты за 1 с. Атмосферное давление 1,01·10 5 Па. Температура окружающей среды 27 0С, молярная масса воздуха 0,029 кг/моль.
Дано:
Найти:
Решение Согласно уравнению (II.9), концентрация молекул воздуха
Число молекул, ударяющихся о стенку за 1 с
где среднеквадратичная скорость
ЗАДАЧА № II.30 Откаченная лампа накаливания объёмом 10 см3 имеет трещину, в которую проникает 106 частиц газа за 1с. Сколько времени понадобится, чтобы в лампе установилось нормальное давление? Температура 0 0С.
Дано:
Найти:
Решение В лампе при нормальном давлении находится
где Считая скорость проникновения мо
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.186.110 (0.011 с.) |

 занимаемым им объемом
занимаемым им объемом  давлением
давлением  оказываемым газом на стенки сосуда, температурой
оказываемым газом на стенки сосуда, температурой 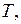 при которой находится газ, а также его молярной массой m. Уравнения, которые связывают между собой эти величины, называются газовыми законами.
при которой находится газ, а также его молярной массой m. Уравнения, которые связывают между собой эти величины, называются газовыми законами. и
и 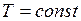

 . (II.1)
. (II.1)
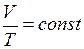 . (II.2)
. (II.2)
 . (II.3)
. (II.3) . (II.4)
. (II.4)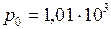 Па,
Па,  К,
К,  м3 (объем 1 моль любого газа при нормальных условиях).
м3 (объем 1 моль любого газа при нормальных условиях).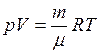 , (II.5)
, (II.5) – масса газа;
– масса газа; 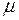 - молярная масса газа;
- молярная масса газа; , (II.6)
, (II.6)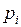 – парциальные давления компонент смеси.
– парциальные давления компонент смеси. показан замкнутый процесс 1–2–3–1. Изобразите этот процесс на
показан замкнутый процесс 1–2–3–1. Изобразите этот процесс на  и
и 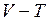 диаграммах.
диаграммах.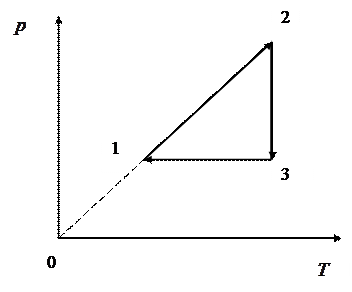

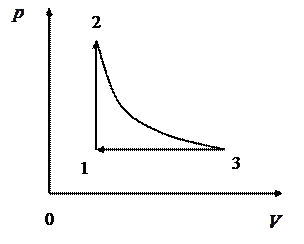





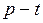 Рисунок 21 – Диаграмма
Рисунок 21 – Диаграмма  .
.

 , где
, где 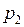 меньше
меньше 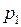 за счет откачки воздуха при постоянном гидростатическом давлении.
за счет откачки воздуха при постоянном гидростатическом давлении. . Из уравнения
. Из уравнения следует, что приращение
следует, что приращение 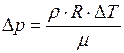 независит от объема колбы.
независит от объема колбы.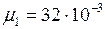 кг/моль;
кг/моль; кг/моль;
кг/моль; .
.
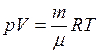 . (1)
. (1)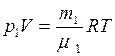 , (2)
, (2)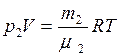 , (3)
, (3) Складывая (2) и (3), получим
Складывая (2) и (3), получим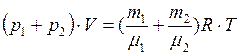 (4)
(4) ,имеем
,имеем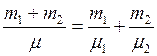 , откуда
, откуда . (5)
. (5) ,
,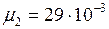 кг/моль.
кг/моль.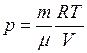 .
.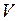 и температуру
и температуру 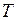 газа уменьшить вдвое, то давление газа, как видно из уравнения, не изменится.
газа уменьшить вдвое, то давление газа, как видно из уравнения, не изменится.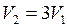 ;
;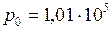 Па;
Па;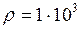 кг/м3.
кг/м3.
 ,
,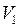 ,
, 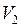 – объемы пузырьков у дна и поверхности озера.
– объемы пузырьков у дна и поверхности озера.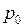 , т.е.
, т.е.  . Тогда
. Тогда 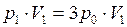 , откуда
, откуда  .
.

 - плотность воды;
- плотность воды;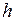 – глубина озера.
– глубина озера.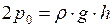
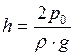 ;
; 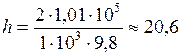 м.
м.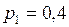 МПа
МПа 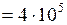 Па;
Па; л
л  м3;
м3;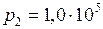 Па.
Па.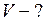
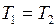 и подчиняется закону Бойля – Мариотта, для которого справедливо уравнение (II.1), или
и подчиняется закону Бойля – Мариотта, для которого справедливо уравнение (II.1), или 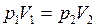 . Но после присоединения второго сосуда газ занял объём
. Но после присоединения второго сосуда газ занял объём  , следовательно,
, следовательно,  , или
, или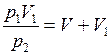 , откуда
, откуда  ; Подстановка численных данных
; Подстановка численных данных м3 . Вместимость второго сосуда
м3 . Вместимость второго сосуда 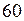 л.
л.
 К;
К; ;
;
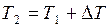 . При этом объём газа увеличился от V1 до V2, т.е.
. При этом объём газа увеличился от V1 до V2, т.е. 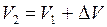 . Так как процесс протекает при постоянном давлении р2=р1, то уравнение состояния
. Так как процесс протекает при постоянном давлении р2=р1, то уравнение состояния  преобразуется
преобразуется  , или
, или . Решение этого уравнения относительно Т1 дает
. Решение этого уравнения относительно Т1 дает .
.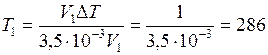 К.
К. ;
;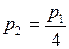 ;
;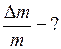
 (1)
(1)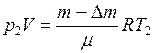 , (2)
, (2) - выпущенная из баллона масса газа. Объём баллона V не изменялся. Выразим объем из (1) уравнения
- выпущенная из баллона масса газа. Объём баллона V не изменялся. Выразим объем из (1) уравнения  и подставим в (2), в результате получим
и подставим в (2), в результате получим  . Сократив одинаковые сомножители и поделив обе части уравнения на
. Сократив одинаковые сомножители и поделив обе части уравнения на  и на
и на  , откуда
, откуда  . Следовательно, из баллона выпустили 25% газа.
. Следовательно, из баллона выпустили 25% газа. и
и  . Как соотносятся эти объёмы газа?
. Как соотносятся эти объёмы газа?
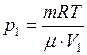 (1) и
(1) и 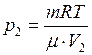 (2)
(2) , а
, а  . Тогда уравнения (1) и (2) примут вид
. Тогда уравнения (1) и (2) примут вид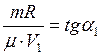 , (3)
, (3) . (4)
. (4) .
.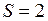 см2
см2  м2;
м2; H;
H; C;
C;  К;
К; МПа
МПа 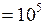 Па.
Па.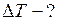
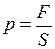 . При нагревании объём не изменяется. По закону Шарля
. При нагревании объём не изменяется. По закону Шарля  , откуда
, откуда  , следовательно,
, следовательно,  . Подстановка численных значений дает
. Подстановка численных значений дает  К.
К.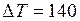 К.
К. .
.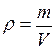 , откуда
, откуда 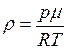 . Если
. Если 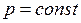 , то
, то  , где
, где  .
.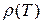 имеет вид гиперболы (рис.25). Если
имеет вид гиперболы (рис.25). Если  , то
, то  , где
, где  , следовательно, плотность изменяется по линейному закону (рис.26).
, следовательно, плотность изменяется по линейному закону (рис.26).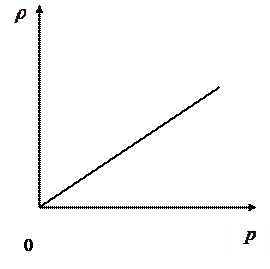

 ;
; 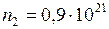 ;
; 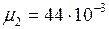 кг/моль;
кг/моль; ;
; 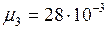 кг/моль;
кг/моль; C;
C; 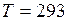 K;
K; 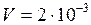 м3.
м3.
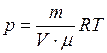 . (1)
. (1)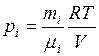 (2)
(2) и
и  – масса и молярная масса отдельного газа. Выразим массу газа
– масса и молярная масса отдельного газа. Выразим массу газа где
где  – число Авогадро и подставим в (2)
– число Авогадро и подставим в (2) .
. , (4)
, (4)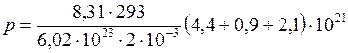
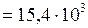 Па.
Па.  кПа.
кПа. , откуда
, откуда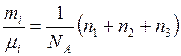 . (5)
. (5)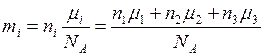 подставим в (5) и получим
подставим в (5) и получим , отсюда
, отсюда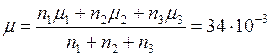 кг/моль.
кг/моль. моль–1, называемое постоянной Авогадро.
моль–1, называемое постоянной Авогадро.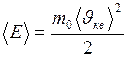 , (II.7)
, (II.7) – масса одной молекулы;
– масса одной молекулы;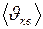 - средняя квадратичная скорость поступательного движения молекул.
- средняя квадратичная скорость поступательного движения молекул. (II.8)
(II.8)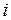 – сумма поступательных и вращательных степеней свободы;
– сумма поступательных и вращательных степеней свободы;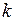 – постоянная Больцмана;
– постоянная Больцмана; (II.9)
(II.9) .
. 2)
2)  .
.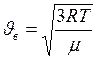 , а
, а 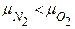 .
. будут одинаковые. Однако, молекул водорода при одинаковых массах и объемов больше, поэтому водород создает большее давление. А для того чтобы давление было одинаковым, объём занимаемый кислородом, необходимо уменьшить в 16 раз
будут одинаковые. Однако, молекул водорода при одинаковых массах и объемов больше, поэтому водород создает большее давление. А для того чтобы давление было одинаковым, объём занимаемый кислородом, необходимо уменьшить в 16 раз 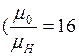 ).
).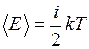 . Молекула водяного пара многоатомная и имеет степеней свободы i = 6 (3 поступательных + 3 вращательных). Средняя энергия, приходящаяся на одну степень свободы
. Молекула водяного пара многоатомная и имеет степеней свободы i = 6 (3 поступательных + 3 вращательных). Средняя энергия, приходящаяся на одну степень свободы  . Следовательно,
. Следовательно,  .
.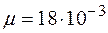 кг/моль;
кг/моль; г
г 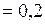 кг;
кг;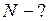
 молекул.
молекул. кг/м3;
кг/м3; м/с.
м/с.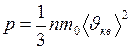 .
. выражает массу молекул, содержащихся в единице объема вещества и, следовательно, равно плотности газа
выражает массу молекул, содержащихся в единице объема вещества и, следовательно, равно плотности газа  .Таким образом,
.Таким образом, Па.
Па. C;
C;  К;
К; м/с;
м/с;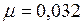 кг/моль.
кг/моль.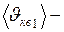 ?
? 
 .
.
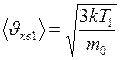 .
. то уравнение для скорости, можно переписать в виде
то уравнение для скорости, можно переписать в виде м/с.
м/с. :
:  и выразим из него
и выразим из него  К.
К.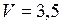 л
л 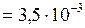 м3;
м3; ;
; ;
;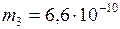 кг;
кг;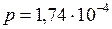 мм.рт.ст.
мм.рт.ст. 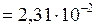 Па;
Па;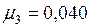 кг/моль.
кг/моль.
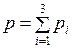 ,
,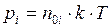 ;
;  – концентрация
– концентрация  ;
;  – число молекул
– число молекул 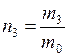 (
(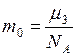 – масса одной молекулы аргона.) Тогда
– масса одной молекулы аргона.) Тогда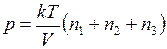
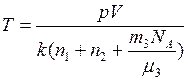 .
. 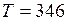 К.
К. см 2
см 2 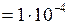 м2;
м2; C;
C; 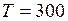 К;
К;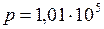 Па.
Па.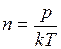 .
. 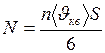 , (2)
, (2)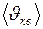
 , а число 6 в знаменателе означает
, а число 6 в знаменателе означает 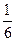 направлений в пространстве. Подставляя (1) в (2), получим
направлений в пространстве. Подставляя (1) в (2), получим ;
;  с-1.
с-1. см3
см3  м3;
м3;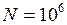 c – 1;
c – 1;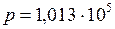 Па;
Па; 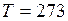 К.
К.
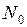 число молекул
число молекул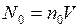 ,
, – концентрация молекул, определяемая из уравнения
– концентрация молекул, определяемая из уравнения 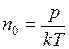 . Тогда число молекул будет равно
. Тогда число молекул будет равно  .
.


