
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон максвелла распределения молекул по скоростямСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте При введении средней квадратичной скорости справедливо полагалось, что даже в состоянии термодинамического равновесия молекулы обладают различными скоростями. Закон Максвелла позволяет определить число молекул идеального газа, значения скоростей которых лежат в некотором интервале.
¨ Функция распределения
Здесь ¨ Закон распределения молекул идеального газа по скоростям получен Максвеллом с применением методов теории вероятностей
где ¨ График функции распределения (рис. 8.2) имеет явный максимум:
¨ Наиболее вероятная скорость молекул
Найдем
Наиболее вероятная скорость — это скорость, которой обладает наибольшее число молекул газа. ¨ Средняя арифметическая скорость молекул определяется по формуле
Действительно,
Барометрическая формула Атмосфера Земли существует за счет земного притяжения молекул воздуха и их теплового движения.
¨ Барометрическая формула — это закон изменения атмосферного
Здесь ¨ Вывод барометрической формулы. Полагаем, что атмосфера представляет собой идеальный газ с одинаковой массой всех его молекул. Ускорение свободного падения Давление столба газа (жидкости) высотой h: Выразим плотность из уравнения Клапейрона-Менделеева
¨ Распределение Больцмана для внешнего потенциального поля: при постоянной температуре плотность (
Действительно, т.к. уравнение состояния Распределение Максвелла — распределение молекул по значениям кинетической энергии, а распределение Больцмана — по значениям потенциальной энергии.
Явления переноса Процессы, протекающие в неравновесных газовых системах, носят необратимый характер. К таким процессам относятся явления переноса: диффузия, теплопроводность и внутреннее трение. Любая система при нормальных условиях состоит из огромного числа (
¨ Среднее число столкновений молекулы газа
определяется количеств Здесь учтено, что образующая цилиндра (рис. 8.4) равна расстоянию, проходящему молекулой за одну секунду, т.е. численно равна средней арифметической скорости. При нормальных условиях ¨ Средняя длина свободного пробега молекулы
Считая, что за 1с молекула пройдет путь, равный средней арифметической скорости ¨ Диффузия — это выравнивание плотности системы, обусловленное переносом массы вещества. Диффузия — самопроизвольное проникновение частиц соприкасающихся веществ друг в друга. При этом происходит перенос вещества из областей с большей концентрацией в области с меньшей концентрацией молекул. Рассмотрим простейший одномерный случай диффузии, когда плотность газа меняется только вдоль одной координаты: Явление диффузии для однородного газа подчиняется закону Фика:
Здесь Коэффициент диффузии зависит от природы газов и физических условий, т.е. давления, температуры системы. Несмотря на огромную скорость молекул газа, диффузия протекает медленно. Это объясняется непрерывными столкновениями молекул, приводящими к зигзагообразному их движению.
¨ Теплопроводность — это выравнивание температуры системы, обусловленное переносом энергии. Если в одной области газа средняя кинетическая энергия молекул (температура) больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания кинетических энергий молекул. Осуществляется перенос энергии в форме теплоты. Полагаем, что температура меняется только вдоль одной координаты: Теплопроводность подчиняется закону Фурье:
Здесь Коэффициент теплопроводности зависит от природы газа и физических условий: давления, температуры, плотности и молярной теплоемкости
¨ Внутреннее трение — выравнивание скоростей молекул различных слоев системы, обусловленное переносом импульса. Внутреннее трение возникает между параллельными слоями жидкости или газа, движущимися с различными скоростями. В каждом слое молекулы участвуют в двух движениях: тепловом хаотическом и направленном вместе со слоем. Тепловое движение перебрасывает молекулы из одного слоя в другой. При этом импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее — увеличивается. Внутреннее трение подчиняется закону Ньютона:
Здесь Процессы переноса переводят материю в состояние предельной дезорганизации (хаоса), которым является термодинамическое равновесие.
Глава 9 ОСНОВЫ ТЕРМОДИНАМИКИ Термодинамика изучает наиболее общие свойства физических систем, не рассматривая внутреннее микроскопическое строение вещества. В основе термодинамики лежат фундаментальные законы или начала, установленные в результате обобщения экспериментальных данных.
Внутренняя энергия ¨ Число степеней свободы
· Одноатомная молекула (рис. 9.1) имеет · · Многоатомная молекула обладает ¨ Закон равнораспределения энергии по степеням свободы:на каждую степень свободы молекулы приходится в среднем кинетическая энергия ¨ Внутренняя энергия идеального газа U — это кинетическая энергия поступательного и вращательного движения всех его молекул.
Т.к. для N молекул газа счислом степеней свободы Внутренняя энергия системы зависит только от абсолютной температуры
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 793; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |

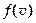 молекул по скоростям — это относительное число молекул, скорости которых лежит в интервале от
молекул по скоростям — это относительное число молекул, скорости которых лежит в интервале от 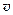 до
до 
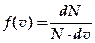 .
.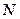 — число молекул в некотором объёме газа, dN — число молекул, скорости которых лежат в интервале от
— число молекул в некотором объёме газа, dN — число молекул, скорости которых лежат в интервале от 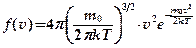 ,
, — масса молекулы,
— масса молекулы,  — постоянная Больцмана, Т — абсолютная температура.
— постоянная Больцмана, Т — абсолютная температура. Относительное число
Относительное число 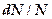 молекул со скоростями в интервале от
молекул со скоростями в интервале от  .
.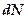 молекул с очень малыми
молекул с очень малыми 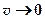 и очень большими
и очень большими  скоростями крайне мало, т.к. при этих скоростях
скоростями крайне мало, т.к. при этих скоростях 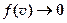 .
. Площадь (рис. 8.2), ограниченная кривой
Площадь (рис. 8.2), ограниченная кривой  и осью скоростей
и осью скоростей  .
.  — скорость, при которой функция распределения (рис. 8.2) принимает максимальное значение
— скорость, при которой функция распределения (рис. 8.2) принимает максимальное значение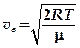 .
. , исследуя
, исследуя 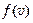 на экстремум. При этом коэффициент, независящий от скорости
на экстремум. При этом коэффициент, независящий от скорости 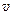 не учитываем.
не учитываем.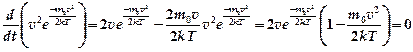 Полученное выражение равно нулю при
Полученное выражение равно нулю при  и
и  . Однако при таких скоростях функция распределения, как было отмечено выше, стремится к минимуму. Следовательно, указанные решения не имеют физического смысла. Тогда должно выполняться условие
. Однако при таких скоростях функция распределения, как было отмечено выше, стремится к минимуму. Следовательно, указанные решения не имеют физического смысла. Тогда должно выполняться условие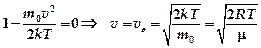 , т.к.
, т.к. 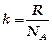 и
и 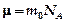 .
.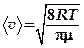 .
.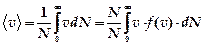 . Подставив сюда
. Подставив сюда  .Значения средней арифметической скорости больше наиболее вероятной, но меньше средней квадратичной скорости:
.Значения средней арифметической скорости больше наиболее вероятной, но меньше средней квадратичной скорости:  .
.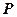 давления с высотой
давления с высотой 
 .
. — давление на высоте
— давление на высоте 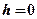 ,
, 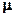 — молярная масса воздуха,
— молярная масса воздуха, 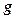 ускорение свободного падения, R — универсальная газовая постоянная. Эта формула позволяет вычислить давление на заданной высоте и, наоборот, по известному давлению определять высоту.
ускорение свободного падения, R — универсальная газовая постоянная. Эта формула позволяет вычислить давление на заданной высоте и, наоборот, по известному давлению определять высоту.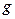 и температура
и температура 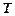 не зависят от высоты.
не зависят от высоты.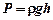 . При увеличении высоты на
. При увеличении высоты на 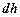 атмосферное давление уменьшится на
атмосферное давление уменьшится на  , следовательно:
, следовательно:  .
. . Тогда
. Тогда 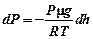 , или
, или  . Полагая
. Полагая 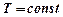 , интегрируем обе части уравнения, считая, что с изменением высоты от
, интегрируем обе части уравнения, считая, что с изменением высоты от 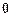 до
до 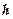 давление меняется от
давление меняется от 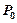 до
до 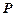 :
: . Воспользовавшись определением логарифма, получим барометрическую формулу.
. Воспользовавшись определением логарифма, получим барометрическую формулу.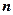 — концентрация) газа больше там, где меньше потенциальная энергия его молекул
— концентрация) газа больше там, где меньше потенциальная энергия его молекул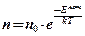 .
.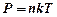 , где
, где 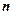 — концентрация молекул на высоте
— концентрация молекул на высоте 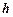 , то барометрическая формула принимает вид:
, то барометрическая формула принимает вид: 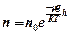 . Распределение Больцмана получим, преобразуя показатель степени и учитывая, что
. Распределение Больцмана получим, преобразуя показатель степени и учитывая, что 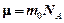 и
и  :
:  , где
, где 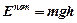 — потенциальная энергия молекулы.
— потенциальная энергия молекулы.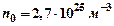 — число Лошмидта) молекул диаметром
— число Лошмидта) молекул диаметром 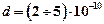 м.
м.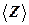 за единицу времени
за единицу времени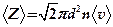
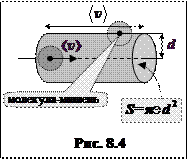 ом молекул, находящихся (рис. 8.4) в цилиндре объемом
ом молекул, находящихся (рис. 8.4) в цилиндре объемом  , т.е.
, т.е.  , где
, где 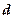 — диаметр и
— диаметр и  — средняя арифметическая скорость молекулы, п — концентрация молекул. С учетом движения остальных молекул число столкновений увеличится в
— средняя арифметическая скорость молекулы, п — концентрация молекул. С учетом движения остальных молекул число столкновений увеличится в 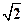 .
. м/с и за
м/с и за  с молекула претерпевает
с молекула претерпевает 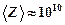 столкновений.
столкновений. — это расстояние, пройденное между двумя последовательными соударениями
— это расстояние, пройденное между двумя последовательными соударениями .
.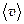 , испытав при этом
, испытав при этом  соударений, получаем
соударений, получаем 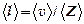 искомое соотношение. При нормальных условиях
искомое соотношение. При нормальных условиях 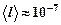 м.
м.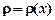 . Ось
. Ось 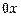 ориентирована в направлении переноса.
ориентирована в направлении переноса.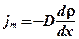 .
.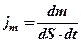 — плотность потока массы — массы вещества, диффундирующего в единицу времени через единицу площади, перпендикулярную направлению переноса, т.е. оси
— плотность потока массы — массы вещества, диффундирующего в единицу времени через единицу площади, перпендикулярную направлению переноса, т.е. оси 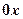 ;
;  — коэффициент диффузии.
— коэффициент диффузии.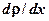 — градиент плотности — скорость изменения плотности вдоль направления диффузии. Знак минус означает, что масса переносится в сторону убывания плотности.
— градиент плотности — скорость изменения плотности вдоль направления диффузии. Знак минус означает, что масса переносится в сторону убывания плотности.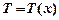 .
. .
.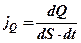 — плотность теплового потока — количество энергии, переносимой в форме теплоты, в единицу времени через единицу площади, перпендикулярную направлению переноса;
— плотность теплового потока — количество энергии, переносимой в форме теплоты, в единицу времени через единицу площади, перпендикулярную направлению переноса; 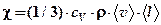 — коэффициент теплопроводности.
— коэффициент теплопроводности.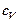 при постоянном объеме.
при постоянном объеме. — градиент температуры — скорость изменения температуры в направлении теплопроводности. Знак минус означает, что энергия переносится в направлении убывания температуры.
— градиент температуры — скорость изменения температуры в направлении теплопроводности. Знак минус означает, что энергия переносится в направлении убывания температуры.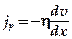 .
.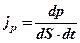 — плотность потока импульса — полный импульс, переносимый в единицу времени через единицу площади, перпендикулярную направлению переноса;
— плотность потока импульса — полный импульс, переносимый в единицу времени через единицу площади, перпендикулярную направлению переноса; 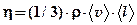 — коэффициент внутреннего трения (динамическая вязкость);
— коэффициент внутреннего трения (динамическая вязкость); 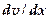 — градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости,
— градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости, 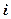 — это число независимых координат, определяющих положение молекулы в пространстве.
— это число независимых координат, определяющих положение молекулы в пространстве.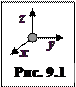 Материальная точка, движущаяся вдоль одной оси координат, имеет одну степень свободы. Материальная точка на плоскости имеет две степени свободы, т.к. для определения ее положения нужно знать две координаты
Материальная точка, движущаяся вдоль одной оси координат, имеет одну степень свободы. Материальная точка на плоскости имеет две степени свободы, т.к. для определения ее положения нужно знать две координаты 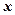 и
и 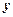 .
.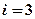 , т.к. это материальная точка, способная двигаться вдоль осей
, т.к. это материальная точка, способная двигаться вдоль осей 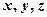 .
.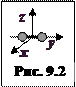 Двухатомная молекула (рис. 9.2) имеет
Двухатомная молекула (рис. 9.2) имеет 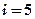 , т.к. состоит из 2-х жестко связанных материальных точек, способных двигаться вдоль трех координатных осей
, т.к. состоит из 2-х жестко связанных материальных точек, способных двигаться вдоль трех координатных осей  (вращение вокруг третьей оси
(вращение вокруг третьей оси  лишено смыслы, т.к. момент инерции
лишено смыслы, т.к. момент инерции  );
);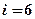 — три поступательных и три вращательных.
— три поступательных и три вращательных. , где
, где  — постоянная Больцмана, R — газовая постоянная, NA — число Авогадро.
— постоянная Больцмана, R — газовая постоянная, NA — число Авогадро.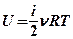 .
.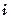
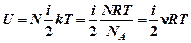 , где
, где 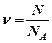 — количества вещества, т.е. число молей газа.
— количества вещества, т.е. число молей газа.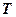 . В общем случае внутренняя энергия — это энергия теплового хаотического движения микрочастиц системы, а также энергия взаимодействия этих частиц. Поскольку молекулы идеального газа не взаимодействуют между собой на расстоянии, то их потенциальная энергия равна нулю. Колебательные движения молекул идеального газа не учитываются, т.к. считается, что атомы молекул жестко связаны между собой.
. В общем случае внутренняя энергия — это энергия теплового хаотического движения микрочастиц системы, а также энергия взаимодействия этих частиц. Поскольку молекулы идеального газа не взаимодействуют между собой на расстоянии, то их потенциальная энергия равна нулю. Колебательные движения молекул идеального газа не учитываются, т.к. считается, что атомы молекул жестко связаны между собой.


