
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Второй закон Ньютона для вращательного движенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим вращательное движение твердого тела относительно неподвижной оси. ¨ Момент силы — мера силового взаимодействия между телами при вращательном движении. Момент силы является аналогом силы при поступательном движении тел. ¨ Модуль момента силы равен произведению силы на плечо
где
Единица вращающего момента — ньютон на метр, (Н∙м). Момент силы ¨ Результирующий момент внешних сил равен векторной сумме моментов всех внешних сил, действующих на тело
¨ Момент инерции I является мерой инертности тел во вращательном движении и зависит от массы тела и ее распределения относительно оси вращения.
где
Действительно, для всех материальных точек
Поскольку в диске по сравнению с кольцом часть массы смещена к оси вращения, то его момент инерции уменьшается.
¨ Теорема Штейнера: момент инерции
¨ Второй закон Ньютона для вращательного движения: угловое ускорение
Вектор углового ускорения (рис. 4.3) направлен вдоль вектора результирующего момента сил.
На материальную точку (рис. 4.4) массой
где
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 1701; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.116.134 (0.011 с.) |

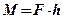 ,
, — плечо силы — длина перпендикуляра (рис. 4.1), опущенного от оси вращения на линию действия силы.
— плечо силы — длина перпендикуляра (рис. 4.1), опущенного от оси вращения на линию действия силы. Момент силы, вращающий тело против хода часовой стрелки (рис. 4.1), считается положительным, по ходу — отрицательным.
Момент силы, вращающий тело против хода часовой стрелки (рис. 4.1), считается положительным, по ходу — отрицательным. является псевдовектором и направлен вдоль оси вращения (рис. 4.1) в соответствие с правилом правого винта.
является псевдовектором и направлен вдоль оси вращения (рис. 4.1) в соответствие с правилом правого винта.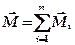 .
. , вращающейся по окружности радиуса
, вращающейся по окружности радиуса 
 .
.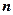 составляющих его материальных точек
составляющих его материальных точек ,
, — масса
— масса 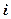 -ой материальной точки и
-ой материальной точки и  — расстояние от нее до оси вращения.
— расстояние от нее до оси вращения. относительно оси симметрии
относительно оси симметрии .
. , следовательно
, следовательно .
. .
. .
. относительно оси, перпендикулярной стержню и проходящей через его середину
относительно оси, перпендикулярной стержню и проходящей через его середину .
. тела (рис. 4.2) относительно произвольной оси
тела (рис. 4.2) относительно произвольной оси  , параллельной оси симметрии
, параллельной оси симметрии  ,
,  равен сумме момента инерции
равен сумме момента инерции  тела относительно оси
тела относительно оси  .
. , приобретаемое телом, пропорционально вращающему моменту
, приобретаемое телом, пропорционально вращающему моменту  и обратно пропорционально моменту инерции
и обратно пропорционально моменту инерции  тела.
тела.
 Используя аналогию поступательного и вращательного движений, можно заключить, что вызываемое у тел ускорение
Используя аналогию поступательного и вращательного движений, можно заключить, что вызываемое у тел ускорение  пропорционально мере взаимодействия между телами (
пропорционально мере взаимодействия между телами (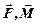 ) и обратно пропорционально мере инертности
) и обратно пропорционально мере инертности 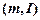 тел.
тел.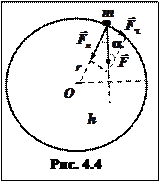 ¨ Вывод второго закона Ньютона для вращательного движения.
¨ Вывод второго закона Ньютона для вращательного движения. , способную вращаться по окружности радиуса
, способную вращаться по окружности радиуса  , действует сила
, действует сила  . Согласно второму закону Ньютона тело под действием тангенциальной составляющей силы приобретает ускорение
. Согласно второму закону Ньютона тело под действием тангенциальной составляющей силы приобретает ускорение  . Учитывая, что
. Учитывая, что  и
и  (формула связи тангенциального и углового ускорений), получаем
(формула связи тангенциального и углового ускорений), получаем  . Умножим на
. Умножим на 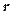 обе части уравнения
обе части уравнения ,
, — момент силы,
— момент силы, 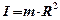 — момент инерции материальной точки.
— момент инерции материальной точки.


