
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематические уравнения поступательного движенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МЕХАНИКА Механика изучает закономерности механического движения и взаимодействия тел. Механическое движение — изменение взаимного расположения тел с течением времени.
Глава 1 КИНЕМАТИКА Кинематика изучает движение тел, не рассматривая причины самого движения. Движение любого тела можно представить в виде комбинации поступательного и вращательного движений. При поступательном движении прямая, проведенная на теле, перемещается параллельно своему первоначальному положению.
Скорость Скорость характеризует быстроту движения, т.е. изменение положения тела в единицу времени. При движении тела меняются координаты, путь и радиус-вектор. Следовательно, должно существовать несколько определений скорости.
Вектор средней скорости(рис. 1.3) направлен вдоль перемещения. При движении тела по замкнутой траектории перемещение
¨ Мгновенная скорость
Вектор мгновенной скорости направлен по касательной к траектории (рис. 1.3) в сторону движения тела. Действительно, перемещение Мгновенная скорость — это скорость в данный момент времени и равна предельному значению средней скорости (рис. 1.3) при неограниченном уменьшении промежутка времени
Т.к. при движении меняются координаты тела, то можно указать скорости изменения этих координат, т.е. найти проекции мгновенной скорости на оси координат. Действительно, дифференцируя по времени принцип суперпозиции, получаем
¨ Модуль мгновенной скорости определяется (рис. 1.4) с использованием значений проекций скорости
¨ Закон сложения скоростей: если тело одновременно участвует в нескольких движениях со скоростями
¨ Средняя путевая скорость — это отношение пути
Единица скорости в СИ — метр в секунду (м/с). ¨ Путевая (скалярная) скорость — это первая производная длины пути по времени
Путевая скорость равна модулю мгновенной скорости. Т.к. ¨ Задача 2. Использовать условие задачи 1. Задание 1. Определить среднюю скорость Решение. По определению средняя скорость Задание 2. Определить мгновенную скорость Решение. По определению мгновенная скорость
Ускорение Ускорение — это быстрота изменения скорости. При движении скорость тела может меняться как по величине — разгон, торможение, так и по направлению — поворот. Характеристикой изменения скорости движения тела со временем является ускорение. Аналогично скоростям вводятся следующие ускорения. ¨ Мгновенное ускорение
Здесь учтено, что Единица ускорения — метр на секунду в квадрате (м/с2). ¨ Проекции вектора ускорения на оси координат равны первым производным соответствующих проекций скоростей или вторым производным соответствующих координат по времени
Действительно, разложив ускорение ¨ Модуль вектора ускорения
¨ Тангенциальная и нормальная составляющие ускорения. В общем случае, ускорение
Тангенциальное ускорение
Нормальное ускорение
где ¨ Вывод формулы модуля нормального ускорения. Пусть материальная точка движется по окружности радиусом
Изменение скорости
¨ Задача 3. Использовать условие задачи 1. Задание. Рассчитать полное Решение. Полное ускорение Для определения тангенциального
направлено вертикально вниз, поскольку  а а  имеет отрицательную величину. Тангенциальное имеет отрицательную величину. Тангенциальное  и нормальное и нормальное  ускорения являются составляющими полного ускорения ускорения являются составляющими полного ускорения  и направлены соответственно вдоль и перпендикулярно вектору мгновенной скорости и направлены соответственно вдоль и перпендикулярно вектору мгновенной скорости  (рис. 1.7). Отмеченные углы (рис. 1.7). Отмеченные углы  равны как накрест лежащие. Из подобия выделенных треугольников следует, что равны как накрест лежащие. Из подобия выделенных треугольников следует, что  и и  Подставив значения ускорения и скоростей для момента времени Подставив значения ускорения и скоростей для момента времени  : :  , ,  , , 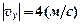 , ,  , получим: , получим:  , ,  . Проверка: . Проверка:  . .
Прямолинейное движение Прямолинейным называется движение, при котором нормальное ускорение ¨ Равнопеременное движение — движение, при котором тангенциальное ускорение ¨ Скорость тела при равнопеременном движении
Здесь полагаем, что проекция начальной скорости По определению проекция ускорения ¨ Кинематическое уравнение равнопеременного движения
Действительно, проекция скорости ¨ Равномерное движение — движение, при котором тангенциальное ускорение
и его координата
¨ Графическое представление кинематических характеристик (рис. 1.8, 1.9, 1.10).
Глава 2 Первый закон Ньютона ¨ Первый закон Ньютона: тело покоится или движется равномерно и прямолинейно до тех пор, пока на него не подействуют другие тела. Стремление тела сохранять свою скорость называется инертностью, а движение тела, свободного от воздействия других тел, — движением по инерции. Первый закон Ньютона выполняется только в инерциальных системах отсчета — системах, вектор скорости которых не меняется с течением времени. ¨ Инерциальная система отсчета — это система, в которой выполняется первый закон Ньютона, т.е. свободная материальная точка либо покоится, либо движется равномерно и прямолинейно. Любая система отсчета, движущаяся равномерно и прямолинейно относительно некоторой инерциальной системы, также является инерциальной. Можно заключить, что инерциальных систем множество. Все инерциальные системы эквивалентны. Однако в одних инерциальных системах тело может покоиться, в других двигаться. Следовательно, механическое движение относительно. Системы отсчета, движущиеся с ускорением, называются неинерциальными, например, тормозящий автобус. В дальнейшем мы будем использовать только инерциальные системы отсчета. ¨ Инертность — способность тела сохранять свою скорость. Действительно, чем труднее изменить скорость тела, тем более инертным оно считается. Вместе с тем, труднее всего изменить скорость наиболее массивного тела. ¨ Масса Масса — аддитивная величина, т.е. масса системы равна сумме масс тел, входящих в эту систему.
Силы в механике В современной физике все взаимодействия сводятся к четырем фундаментальным. Это гравитационное, электромагнитное, сильное и слабое взаимодействия. Сильное взаимодействиеобеспечивает внутриядерные связи и является самым сильным в природе. Слабое взаимодействиеприсуще всем частицам, кроме фотона, и определяет радиоактивный распад и реакции термоядерного синтеза. Механические явления в макроскопическом масштабе определяются гравитационным и электромагнитным взаимодействиями. ¨ Гравитационное взаимодействие обеспечивает притяжение между любыми телами и является универсальным. ¨ Закон всемирного тяготения: две материальные точки притягиваются друг к другу с силой, прямо пропорциональной произведению масс
где ¨ Сила тяжести
¨ Электромагнитное взаимодействие существует только между заряженными частицами, связывая электроны и ядра в атомах, объединяя атомы и молекулы в различные вещества. Силы упругости и трения возникают при изменении межмолекулярной структуры взаимодействующих тел и являются следствием электромагнитного взаимодействия.
где
где
Закон сохранения импульса Введем новую физическую величину — меру количества механического движения. ¨ Импульс тела
Векторы ¨ Основной закон динамики поступательного движения материальной точки: скорость изменения импульса тела равна действующей на него силе
По второму закона Ньютона Т.к. ускорение ¨ Механическая система — это совокупность материальных точек (тел), взаимодействующих между собой с силами, которые называются внутренними силами. Внешние силы — это силы, с которыми внешние тела воздействуют на тела системы. ¨ Импульс
¨ Замкнутая (изолированная) система — система, на которую не действуют внешние силы. ¨ Закон сохранения импульса: импульс замкнутой системы тел не меняется с течением времени
Рассмотрим две налетающие друг на друга материальные точки. При взаимодействии согласно третьему закону Ньютона Следует отметить, что никаких ограничений на обмен импульсами между телами системы нет: одни частицы могут увеличивать свой импульс, другие уменьшать, но суммарный импульс замкнутой системы не меняется. ¨ Центр масс (инерции) системы п материальных точек — это воображаемая точка С, радиус - вектор которой определяется выражением
где ¨ Закон движения центра масс: центр масс механической системы движется как материальная точка массой
Здесь Найдем скорость центра масс ¨ Импульс силы
Это соотношения следует из основного закона динамики и показывает, что изменение импульса тела равно импульсу силы, действующему на это тело.
Глава 3 РАБОТА И ЭНЕРГИЯ Энергия — это количественная мера движения и взаимодействия всех видов материи. Работа — мера превращения одного вида энергии в другой.
Работа и мощность силы Изменить механическое движение тела и, следовательно, его энергию можно лишь под действием силы. Количественной мерой действия силы является работа, которая зависит от величины, направления силы и перемещения тела.
Здесь Единица работы — джоуль (Дж), 1Дж=1Н∙м. ¨ Работа — скалярная величина, знак которой зависит от если ¨ Работа
Для вычисления этого интеграла необходимо знать зависимость силы (рис. 3.2) от пути
¨ Графическое вычисление работы. Работа численно равна площади (рис. 3.2) криволинейной трапеции s 1 abs 2.
Одну и ту же работу можно выполнить за разное время. Быстрота совершения работы называется мощностью. ¨ Мощность N— это работа, совершаемая в единицу времени
Единица мощности — ватт (Вт), 1Вт=1Дж/с. ¨ Мощность силы равна скалярному произведению силы
Т.к. Мощность, как и механическая работа — скалярная величина. Работа и мощность силы зависят от выбора системы отсчета.
Кинетическая энергия Кинетическая энергия представляет один из видов механической энергии. ¨ Кинетическая энергия Для тела массой т,движущегося со скоростью
Для системы
где Кинетическая энергия, как и скорость, величина относительная и зависит от выбора системы отсчета. Единица кинетической энергии — джоуль (Дж). ¨ Теорема о кинетической энергии: работа внешней силы равна изменению кинетической энергии тела:
По определению
Т.о., изменить кинетическую энергию тела можно только за счет работы, совершаемой внешней силой.
Потенциальная энергия Потенциальная энергия — это один из видов механической энергии. ¨ Потенциальная энергия U — энергиявзаимодействия тел, зависящая от их расположения в силовом поле. Силовыми являются, например, гравитационные и электромагнитные поля, в которых на тело в каждой точке пространства действует определенная сила. ¨ Консервативные силы — силы,работа которых не зависит от вида траектории движения, а определяется только начальным и конечным положениями тела. Поле, в котором действуют только консервативные силы, называется потенциальным полем. Потенциальным является поле сил тяжести Земли, электростатическое поле. К неконсервативным или диссипативным силам относятся, например, силы трения. Работа диссипативных сил уменьшает механическую энергию, переводя ее в другие виды, например, во внутреннюю энергию. ¨ Потенциальная энергия тела массой т на высоте h над поверхностью Земли
где Потенциальная энергия зависит от выбора системы отсчета и может иметь отрицательное значение. Так если принять за нуль потенциальную энергию тела на поверхности Земли, то потенциальная энергия тела на дне шахты будет отрицательной. ¨ Сила тяжести Доказательство. Найдем работу
то Работа силы тяжести не зависит от вида траектории движения и определяется только начальной ¨ Работа консервативных сил равна уменьшению потенциальной энергии тела.
Действительно, т.к. ¨ Связь консервативной силы и потенциальной энергии.
Знак минус означает, что сила направлена в сторону убывания потенциальной энергии. Доказательство. Пусть частица находится в поле консервативных сил (например, в гравитационном), и ее потенциальная энергия зависит только от одной координаты ¨ Потенциальная энергия деформированной пружины
Доказательство. Т.к.
Закон сохранения энергии ¨ Закон сохранения механической энергии
В представленном законе Доказательство. Рассмотрим тело, движущееся под действием только консерв
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 1199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.27.70 (0.01 с.) |


 ¨ Средняя скорость
¨ Средняя скорость  — это вектор, равный отношению перемещения
— это вектор, равный отношению перемещения  к продолжительности
к продолжительности  этого перемещения
этого перемещения .
. , и, следовательно, средняя скорость
, и, следовательно, средняя скорость  .
. — это первая производная радиус-векторапо времени
— это первая производная радиус-векторапо времени .
. при уменьшении
при уменьшении  уменьшается (рис. 1.3) и при
уменьшается (рис. 1.3) и при  совпадет со стягиваемой дугой, т.е. будет направлен по касательной к траектории.
совпадет со стягиваемой дугой, т.е. будет направлен по касательной к траектории. .
. ¨ Проекции мгновенной скорости (рис. 1.4) на оси координат — это первые производные соответствующих координат по времени
¨ Проекции мгновенной скорости (рис. 1.4) на оси координат — это первые производные соответствующих координат по времени .
.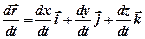 , или
, или .
. .
. , то его результирующая скорость
, то его результирующая скорость  .
. к его продолжительности
к его продолжительности  .
. .
. , то
, то  .
.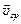 в интервале времени
в интервале времени  .
. . С учетом значений
. С учетом значений  и
и  получаем
получаем 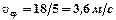 . Направление средней скорости совпадает с направлением вектора перемещения
. Направление средней скорости совпадает с направлением вектора перемещения  (рис. 1.2).
(рис. 1.2). .
. и направлена по касательной к траектории. В момент времени
и направлена по касательной к траектории. В момент времени 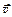 является касательной в точке с координатами (см. таблицу)
является касательной в точке с координатами (см. таблицу)  ,
,  (рис. 1.2). Модуль мгновенной скорости определятся по теореме Пифагора:
(рис. 1.2). Модуль мгновенной скорости определятся по теореме Пифагора:  , где
, где  ,
,  — проекции скорости на оси x и y. Для момента времени
— проекции скорости на оси x и y. Для момента времени  ,
,  (м/с) (знак минус указывает на то, что
(м/с) (знак минус указывает на то, что  направлена в противоположную сторону положительному направлению оси y). Т.о., модуль мгновенной скорости
направлена в противоположную сторону положительному направлению оси y). Т.о., модуль мгновенной скорости  (рис.1.7).
(рис.1.7). — это вектор, равный первой производной скорости
— это вектор, равный первой производной скорости 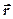 по времени
по времени 
 .
. . Поэтому
. Поэтому 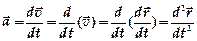 .
. .
. , где
, где  — проекции вектора ускорения.
— проекции вектора ускорения. определяется по теореме Пифагора
определяется по теореме Пифагора .
.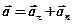 .
. направлено вдоль (против) вектора скорости и характеризует быстроту изменения скорости по величине. Модуль тангенциального ускорения
направлено вдоль (против) вектора скорости и характеризует быстроту изменения скорости по величине. Модуль тангенциального ускорения

 направлено перпендикулярно вектору скорости к центру кривизны траектории и характеризует быстроту изменения скорости по направлению. Модуль нормального ускорения
направлено перпендикулярно вектору скорости к центру кривизны траектории и характеризует быстроту изменения скорости по направлению. Модуль нормального ускорения ,
, — радиус кривизны траектории, или радиус соприкасающейся окружности.
— радиус кривизны траектории, или радиус соприкасающейся окружности. (рис.1.6) с постоянной по величине скоростью
(рис.1.6) с постоянной по величине скоростью .
. по направлению за время
по направлению за время  найдем, осуществив параллельный перенос вектора
найдем, осуществив параллельный перенос вектора  . Указанные треугольники (рис.1.6) подобны, поскольку являются равнобедренными с равными углами
. Указанные треугольники (рис.1.6) подобны, поскольку являются равнобедренными с равными углами 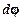 , образованными взаимно перпендикулярными сторонами. Из подобия треугольников находим, что
, образованными взаимно перпендикулярными сторонами. Из подобия треугольников находим, что  , или
, или  . Разделив на
. Разделив на  , или
, или .
. тангенциальное
тангенциальное  и нормальное
и нормальное  ускорения в момент времени
ускорения в момент времени  где
где  и
и  — проекции ускорения на оси x и y. Учитывая, что
— проекции ускорения на оси x и y. Учитывая, что  и
и  (см. задачу 2), получаем:
(см. задачу 2), получаем:  и
и 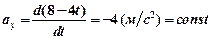 . Полное ускорение
. Полное ускорение  .
.
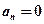 .
. . Если
. Если  , то движение называется равноускоренным, если
, то движение называется равноускоренным, если  — равнозамедленным.
— равнозамедленным.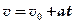 .
. — скорости в момент времени
— скорости в момент времени  совпадает с направлением выбранной оси, например
совпадает с направлением выбранной оси, например  . Для компактности формул индексы скоростей и ускорений не указаны.
. Для компактности формул индексы скоростей и ускорений не указаны. . Интегрируя
. Интегрируя 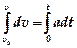 , получаем
, получаем  . Отсюда
. Отсюда  — скорость в момент времени
— скорость в момент времени  .
. .
. Учитывая, что
Учитывая, что  . Интегрируя
. Интегрируя  , имеем
, имеем  , или
, или  — координата движущейся материальной точки в момент времени
— координата движущейся материальной точки в момент времени 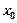 — начальная координата при
— начальная координата при  и, следовательно, скорость тела
и, следовательно, скорость тела
 .
.


 — это мера инертности тела при поступательном движении. Единица массы в СИ — килограмм (кг).
— это мера инертности тела при поступательном движении. Единица массы в СИ — килограмм (кг). и
и  этих точек и обратно пропорциональной квадрату расстояния
этих точек и обратно пропорциональной квадрату расстояния 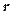 между ними
между ними ,
, — гравитационная постоянная.
— гравитационная постоянная. — это гравитационная сила, сообщающая телу вблизи поверхности Земли ускорение свободного падения
— это гравитационная сила, сообщающая телу вблизи поверхности Земли ускорение свободного падения  . Согласно второму закону Ньютона
. Согласно второму закону Ньютона .
. ¨ Закон трения скольжения: сила трения
¨ Закон трения скольжения: сила трения  скольжения (рис. 2.4) возникает между поверхностями соприкасающихся тел, препятствует их относительному движению и прямо пропорциональна силе реакции опоры
скольжения (рис. 2.4) возникает между поверхностями соприкасающихся тел, препятствует их относительному движению и прямо пропорциональна силе реакции опоры 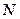
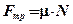 ,
,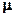 — коэффициент трения скольжения, зависящий от материала соприкасающихся тел и качества обработки их поверхностей. Сила реакции опоры
— коэффициент трения скольжения, зависящий от материала соприкасающихся тел и качества обработки их поверхностей. Сила реакции опоры  согласно третьему закону Ньютона равна по модулю силе нормального давления
согласно третьему закону Ньютона равна по модулю силе нормального давления  тела на плоскость.
тела на плоскость. ¨ Закон Гука:сила упругости
¨ Закон Гука:сила упругости  (рис. 2.5), стремящаяся вернуть тело в исходное состояние, пропорциональна удлинению пружины
(рис. 2.5), стремящаяся вернуть тело в исходное состояние, пропорциональна удлинению пружины 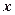 :
: ,
, — начальная и
— начальная и  — конечная длина пружины,
— конечная длина пружины,  , знак минус означает, что сила упругости направлена противоположно удлинению,
, знак минус означает, что сила упругости направлена противоположно удлинению,  — коэффициент жесткости, зависящий от упругих свойств материала и размеров пружины.
— коэффициент жесткости, зависящий от упругих свойств материала и размеров пружины. — это векторная величина, равная произведению массы т тела на его скорость
— это векторная величина, равная произведению массы т тела на его скорость 
 и
и  ).
). .
. .
. , то
, то  . Учитывая, что масса постоянная величина, ее можно внести под знак производной
. Учитывая, что масса постоянная величина, ее можно внести под знак производной  . Полученное соотношение является уравнением движения тела.
. Полученное соотношение является уравнением движения тела. системы п тел массами
системы п тел массами  ,и скоростями
,и скоростями  равен векторной сумме импульсов отдельных тел:
равен векторной сумме импульсов отдельных тел: .
. .
. . С учетом основного закона динамики
. С учетом основного закона динамики  и
и  получаем
получаем  , или
, или  . Производная будет равна нулю, если
. Производная будет равна нулю, если  . Обобщив полученный результат на
. Обобщив полученный результат на 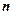 тел, получим искомое соотношение — закон сохранения импульса.
тел, получим искомое соотношение — закон сохранения импульса. ,
,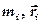 — масса и радиус - вектор
— масса и радиус - вектор 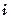 -ой точки соответственно,
-ой точки соответственно,  — масса системы.
— масса системы.
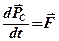 .
. — результирующая внешних сил, приложенных к системе.
— результирующая внешних сил, приложенных к системе. . Отсюда следует
. Отсюда следует  — импульс системы равен импульсу центра масс. Подставив импульс центра масс
— импульс системы равен импульсу центра масс. Подставив импульс центра масс 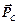 в основной закон динамики, получим искомое соотношение — закон движения центра масс.
в основной закон динамики, получим искомое соотношение — закон движения центра масс. — это произведение силы
— это произведение силы  её действия
её действия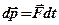 .
. ¨ Элементарная работа
¨ Элементарная работа  силы
силы  — это скалярное произведение
— это скалярное произведение  .
.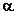 — угол (рис. 3.1) между векторами
— угол (рис. 3.1) между векторами  — проекция силы
— проекция силы  — элементарный путь, пройденный за время
— элементарный путь, пройденный за время  , то
, то  — работа силы тяги всегда положительна, если
— работа силы тяги всегда положительна, если  , то
, то  — работа сил сопротивления всегда отрицательна, если
— работа сил сопротивления всегда отрицательна, если  , то
, то  — работа центростремительных сил или сил реакции опоры равна нулю.
— работа центростремительных сил или сил реакции опоры равна нулю. на конечном участке траектории находится алгебраическим суммированием (интегрированием) элементарных работ на всем пути
на конечном участке траектории находится алгебраическим суммированием (интегрированием) элементарных работ на всем пути .
. на участке 1-2 траектории.
на участке 1-2 траектории.
 — проекция силы на направление движения,
— проекция силы на направление движения, 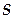 — дуговаякоордината материальной точки, отсчитываемая вдоль траектории.
— дуговаякоордината материальной точки, отсчитываемая вдоль траектории. .
. .
. , то
, то  , где
, где  и скорости
и скорости 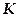 — это энергия механического движения тела (системы).
— это энергия механического движения тела (системы).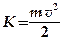 .
.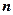 материальных точек
материальных точек ,
, — масса,
— масса,  — скорость
— скорость  .
. Доказательство. Пусть скорость тела (рис. 3.3) массой
Доказательство. Пусть скорость тела (рис. 3.3) массой  под действием силы
под действием силы  до
до  . Найдем работу
. Найдем работу 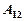 силы
силы  . Т.к.
. Т.к. 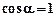 (рис. 3.3) и
(рис. 3.3) и  , то
, то  . Учитывая, что ускорение
. Учитывая, что ускорение 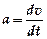 , получаем
, получаем  , или
, или .
. ,
,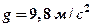 — ускорение свободного падения. Единица потенциальной энергии — джоуль (Дж).
— ускорение свободного падения. Единица потенциальной энергии — джоуль (Дж). является консервативной.
является консервативной. 
 (рис. 3.4) при перемещении тела из
(рис. 3.4) при перемещении тела из  в
в  вдоль произвольной траектории.
вдоль произвольной траектории. . Т.к.
. Т.к.  ,
, .
. и конечной
и конечной  высотой. Следовательно, сила тяжести является консервативной. Из полученного выражения следует, что работа консервативных сил по замкнутой траектории равна нулю.
высотой. Следовательно, сила тяжести является консервативной. Из полученного выражения следует, что работа консервативных сил по замкнутой траектории равна нулю.
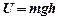 , то соотношение предыдущего пункта принимает вид
, то соотношение предыдущего пункта принимает вид  . Или
. Или  . Знак минус указывает на то, что потенциальная энергия уменьшается.
. Знак минус указывает на то, что потенциальная энергия уменьшается. .
.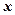 . По определению работа
. По определению работа  . С другой стороны
. С другой стороны  . Из указанных соотношений следует
. Из указанных соотношений следует  — консервативная сила равна градиенту потенциальной энергии с обратным знаком (градиент — скорость изменения потенциальной энергии в пространстве).
— консервативная сила равна градиенту потенциальной энергии с обратным знаком (градиент — скорость изменения потенциальной энергии в пространстве).
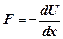 , то
, то 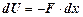 . По закону Гука
. По закону Гука  , тогда
, тогда 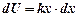 . Интегрируя полученное соотношение, найдем потенциальную энергию пружины с учетом изменения ее длины от
. Интегрируя полученное соотношение, найдем потенциальную энергию пружины с учетом изменения ее длины от 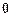 до
до  :
:  . Здесь
. Здесь  — жесткость,
— жесткость,  : полная энергия системы, в которой действуют только консервативные силы, не меняется с течением времени
: полная энергия системы, в которой действуют только консервативные силы, не меняется с течением времени .
. — это кинетическая энергия, и
— это кинетическая энергия, и 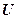 — потенциальная энергия всех тел системы соответственно.
— потенциальная энергия всех тел системы соответственно.


