
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Второй и третий законы НьютонаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ранее выяснили, что тело может изменить свою скорость только под воздействием на него других тел. Всякое воздействие в физике заменяется понятием силы, которая является характеристикой действия одних тел на другие. ¨ Сила Сила полностью определена, если известны её модуль, направление и точка приложения. Прямая, вдоль которой направлен вектор силы, называется линией действия силы.
В дальнейшем под силой, действующей на тело, будем подразумевать результирующую всех сил. ¨ Второй закон Ньютона: ускорение
Вектор ускорения Из представленного соотношения следует, что ¨ Тангенциальная и нормальная составляющие силы.
¨ Третий закон Ньютона: два тела взаимодействуют между собой (рис.2.3) с равными по величине, противоположно направленными силами, приложенными к разным телам
Следует отметить, что при взаимодействии нескольких тел третий закон Ньютона справедлив только для каждой пары тел. В этой связи вопрос, почему трактор тянет плуг, а не наоборот? Действительно, трактор и телега взаимодействуют между собой с равными по величине силами. Однако трактор отталкивается от земли с большей силой, нежели с ней взаимодействует плуг.
Силы в механике В современной физике все взаимодействия сводятся к четырем фундаментальным. Это гравитационное, электромагнитное, сильное и слабое взаимодействия. Сильное взаимодействиеобеспечивает внутриядерные связи и является самым сильным в природе. Слабое взаимодействиеприсуще всем частицам, кроме фотона, и определяет радиоактивный распад и реакции термоядерного синтеза. Механические явления в макроскопическом масштабе определяются гравитационным и электромагнитным взаимодействиями. ¨ Гравитационное взаимодействие обеспечивает притяжение между любыми телами и является универсальным. ¨ Закон всемирного тяготения: две материальные точки притягиваются друг к другу с силой, прямо пропорциональной произведению масс
где ¨ Сила тяжести
¨ Электромагнитное взаимодействие существует только между заряженными частицами, связывая электроны и ядра в атомах, объединяя атомы и молекулы в различные вещества. Силы упругости и трения возникают при изменении межмолекулярной структуры взаимодействующих тел и являются следствием электромагнитного взаимодействия.
где
где
Закон сохранения импульса Введем новую физическую величину — меру количества механического движения.
¨ Импульс тела
Векторы ¨ Основной закон динамики поступательного движения материальной точки: скорость изменения импульса тела равна действующей на него силе
По второму закона Ньютона Т.к. ускорение ¨ Механическая система — это совокупность материальных точек (тел), взаимодействующих между собой с силами, которые называются внутренними силами. Внешние силы — это силы, с которыми внешние тела воздействуют на тела системы. ¨ Импульс
¨ Замкнутая (изолированная) система — система, на которую не действуют внешние силы. ¨ Закон сохранения импульса: импульс замкнутой системы тел не меняется с течением времени
Рассмотрим две налетающие друг на друга материальные точки. При взаимодействии согласно третьему закону Ньютона Следует отметить, что никаких ограничений на обмен импульсами между телами системы нет: одни частицы могут увеличивать свой импульс, другие уменьшать, но суммарный импульс замкнутой системы не меняется. ¨ Центр масс (инерции) системы п материальных точек — это воображаемая точка С, радиус - вектор которой определяется выражением
где ¨ Закон движения центра масс: центр масс механической системы движется как материальная точка массой
Здесь Найдем скорость центра масс ¨ Импульс силы
Это соотношения следует из основного закона динамики и показывает, что изменение импульса тела равно импульсу силы, действующему на это тело.
Глава 3 РАБОТА И ЭНЕРГИЯ Энергия — это количественная мера движения и взаимодействия всех видов материи. Работа — мера превращения одного вида энергии в другой.
Работа и мощность силы Изменить механическое движение тела и, следовательно, его энергию можно лишь под действием силы. Количественной мерой действия силы является работа, которая зависит от величины, направления силы и перемещения тела.
Здесь Единица работы — джоуль (Дж), 1Дж=1Н∙м. ¨ Работа — скалярная величина, знак которой зависит от если
¨ Работа
Для вычисления этого интеграла необходимо знать зависимость силы (рис. 3.2) от пути
¨ Графическое вычисление работы. Работа численно равна площади (рис. 3.2) криволинейной трапеции s 1 abs 2.
Одну и ту же работу можно выполнить за разное время. Быстрота совершения работы называется мощностью. ¨ Мощность N— это работа, совершаемая в единицу времени
Единица мощности — ватт (Вт), 1Вт=1Дж/с. ¨ Мощность силы равна скалярному произведению силы
Т.к. Мощность, как и механическая работа — скалярная величина. Работа и мощность силы зависят от выбора системы отсчета.
Кинетическая энергия Кинетическая энергия представляет один из видов механической энергии. ¨ Кинетическая энергия Для тела массой т,движущегося со скоростью
Для системы
где Кинетическая энергия, как и скорость, величина относительная и зависит от выбора системы отсчета. Единица кинетической энергии — джоуль (Дж). ¨ Теорема о кинетической энергии: работа внешней силы равна изменению кинетической энергии тела:
По определению
Т.о., изменить кинетическую энергию тела можно только за счет работы, совершаемой внешней силой.
Потенциальная энергия Потенциальная энергия — это один из видов механической энергии. ¨ Потенциальная энергия U — энергиявзаимодействия тел, зависящая от их расположения в силовом поле. Силовыми являются, например, гравитационные и электромагнитные поля, в которых на тело в каждой точке пространства действует определенная сила. ¨ Консервативные силы — силы,работа которых не зависит от вида траектории движения, а определяется только начальным и конечным положениями тела. Поле, в котором действуют только консервативные силы, называется потенциальным полем. Потенциальным является поле сил тяжести Земли, электростатическое поле. К неконсервативным или диссипативным силам относятся, например, силы трения. Работа диссипативных сил уменьшает механическую энергию, переводя ее в другие виды, например, во внутреннюю энергию.
¨ Потенциальная энергия тела массой т на высоте h над поверхностью Земли
где Потенциальная энергия зависит от выбора системы отсчета и может иметь отрицательное значение. Так если принять за нуль потенциальную энергию тела на поверхности Земли, то потенциальная энергия тела на дне шахты будет отрицательной. ¨ Сила тяжести Доказательство. Найдем работу
то Работа силы тяжести не зависит от вида траектории движения и определяется только начальной ¨ Работа консервативных сил равна уменьшению потенциальной энергии тела.
Действительно, т.к. ¨ Связь консервативной силы и потенциальной энергии.
Знак минус означает, что сила направлена в сторону убывания потенциальной энергии. Доказательство. Пусть частица находится в поле консервативных сил (например, в гравитационном), и ее потенциальная энергия зависит только от одной координаты ¨ Потенциальная энергия деформированной пружины
Доказательство. Т.к.
Закон сохранения энергии ¨ Закон сохранения механической энергии
В представленном законе Доказательство. Рассмотрим тело, движущееся под действием только консервативной силы, например, силы тяжести. Работа консервативной силы равна изменению потенциальной энергии В этом законе нет запрета на превращения механической энергии из кинетической в потенциальную и наоборот. Так при падении тела его потенциальная энергия за счет работы силы тяжести уменьшается, а кинетическая — возрастает. Однако полная механическая энергия не меняется.
¨ Диссипация (рассеяние) энергии — уменьшение механической энергии за счет работы неконсервативных сил трения. При этом механическая энергия преобразуется в другие формы, например, внутреннюю. Однако полная энергия всех её видов остается неизменной — это закон сохранения энергии в целом.
Соударения Удар или соударение — это кратковременное взаимодействие тел, при котором возникающие силы столь велики, что внешними силами можно пренебречь и рассмотреть соударяющиеся тела как изолированную систему. Удар называется центральным, если тела до удара двигались вдоль прямой, проходящей через их центры масс. ¨ Абсолютно упругий удар — удар, в результате которого тела восстанавливают свою форму, а кинетическая энергия этих тел не меняется.
Запишем законы сохранения кинетической энергии и импульса в проекциях на ось
Группируя по массам
Разделив (1) на (2), выразим
Отсюда находим
Из соотношения
¨ Анализ скоростей шаров после абсолютно упругого удара: · Если массы шаров · Если масса налетающего шара При этом изменение импульса первого шара ¨ Абсолютно неупругий удар — удар, в результате которого тела объединяются и движутся как единое целое, а часть кинетической энергии системы переходит во внутреннюю.
¨ Анализ скорости шаров после абсолютно неупругого удара: · Если: · Если
Задание 1. Определить ускорение Решение. Прежде найдем результирующую силу
Направление оси x выберем вдоль вектора Ускорение
Задание 2. Определить скорость и координату мт в моменты времени Решение. Движение мт прямолинейное равноускоренное. Для такого движения скорость определяется по формуле В момент времени В момент времени Задание 3. Определить импульс мт Решение. Величина импульса тела определяется по формуле Задание 4. Определить работу Решение. Формула механической работы Задание 5. Определить кинетическую энергию мт Решение. Кинетическая энергия определяется по формуле Задание 6. Определить работу Решение. Теореме о кинетической энергии: Задание 7. Определить потенциальную энергию Решение. Выберем начало отсчета потенциальной энергии в точке Задание 8. Определить механическую энергию мт в моменты времени Решение. Механическая энергия в момент времени Т.о., механическая энергия тела, движущегося в поле консервативных сил, не меняется.
Глава 4
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.196.97 (0.017 с.) |

 — это векторная величина, являющаяся мерой взаимодействия между телами при поступательном движении.
— это векторная величина, являющаяся мерой взаимодействия между телами при поступательном движении. ¨ Сложение сил: если на материальную точку (рис. 2.1) действуют несколько сил
¨ Сложение сил: если на материальную точку (рис. 2.1) действуют несколько сил 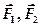 , то их можно заменить результирующей силой
, то их можно заменить результирующей силой  .
. , приобретаемое телом, прямо пропорционально действующей на него силе
, приобретаемое телом, прямо пропорционально действующей на него силе  .
. . Эта формула позволяет определить силу, действующую на тело при решении задач и представить единицу силы: — ньютон (Н);
. Эта формула позволяет определить силу, действующую на тело при решении задач и представить единицу силы: — ньютон (Н);  .
. В общем случае сила
В общем случае сила  , действующая на движущееся тело (рис. 2.2), может быть разложена на тангенциальную
, действующая на движущееся тело (рис. 2.2), может быть разложена на тангенциальную  и нормальную
и нормальную  составляющие, модули которых согласно второму закону Ньютона имеют вид:
составляющие, модули которых согласно второму закону Ньютона имеют вид:  изменяет скорость тела по величине,
изменяет скорость тела по величине,  изменяет скорость тела по направлению. Здесь
изменяет скорость тела по направлению. Здесь 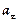 и
и  — тангенциальное и нормальное ускорения соответственно.
— тангенциальное и нормальное ускорения соответственно. .
. Так, налетающие друг на друга шары (рис.2.3), несмотря на различие их масс, и скоростей, при соударении будут воздействовать друг на друга с равными по величине силами.
Так, налетающие друг на друга шары (рис.2.3), несмотря на различие их масс, и скоростей, при соударении будут воздействовать друг на друга с равными по величине силами. и
и  этих точек и обратно пропорциональной квадрату расстояния
этих точек и обратно пропорциональной квадрату расстояния 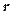 между ними
между ними ,
, — гравитационная постоянная.
— гравитационная постоянная. — это гравитационная сила, сообщающая телу вблизи поверхности Земли ускорение свободного падения
— это гравитационная сила, сообщающая телу вблизи поверхности Земли ускорение свободного падения  . Согласно второму закону Ньютона
. Согласно второму закону Ньютона .
. ¨ Закон трения скольжения: сила трения
¨ Закон трения скольжения: сила трения  скольжения (рис. 2.4) возникает между поверхностями соприкасающихся тел, препятствует их относительному движению и прямо пропорциональна силе реакции опоры
скольжения (рис. 2.4) возникает между поверхностями соприкасающихся тел, препятствует их относительному движению и прямо пропорциональна силе реакции опоры 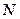
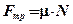 ,
,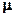 — коэффициент трения скольжения, зависящий от материала соприкасающихся тел и качества обработки их поверхностей. Сила реакции опоры
— коэффициент трения скольжения, зависящий от материала соприкасающихся тел и качества обработки их поверхностей. Сила реакции опоры  согласно третьему закону Ньютона равна по модулю силе нормального давления
согласно третьему закону Ньютона равна по модулю силе нормального давления  тела на плоскость.
тела на плоскость. ¨ Закон Гука:сила упругости
¨ Закон Гука:сила упругости  (рис. 2.5), стремящаяся вернуть тело в исходное состояние, пропорциональна удлинению пружины
(рис. 2.5), стремящаяся вернуть тело в исходное состояние, пропорциональна удлинению пружины 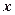 :
: ,
, — начальная и
— начальная и  — конечная длина пружины,
— конечная длина пружины,  , знак минус означает, что сила упругости направлена противоположно удлинению,
, знак минус означает, что сила упругости направлена противоположно удлинению,  — коэффициент жесткости, зависящий от упругих свойств материала и размеров пружины.
— коэффициент жесткости, зависящий от упругих свойств материала и размеров пружины. — это векторная величина, равная произведению массы т тела на его скорость
— это векторная величина, равная произведению массы т тела на его скорость 

 и
и  сонаправлены. Единица импульса — килограмм∙метр в секунду (
сонаправлены. Единица импульса — килограмм∙метр в секунду ( ).
). .
. .
. , то
, то  . Учитывая, что масса постоянная величина, ее можно внести под знак производной
. Учитывая, что масса постоянная величина, ее можно внести под знак производной  . Полученное соотношение является уравнением движения тела.
. Полученное соотношение является уравнением движения тела. системы п тел массами
системы п тел массами  ,и скоростями
,и скоростями  равен векторной сумме импульсов отдельных тел:
равен векторной сумме импульсов отдельных тел: .
. .
. . С учетом основного закона динамики
. С учетом основного закона динамики  и
и  получаем
получаем  , или
, или  . Производная будет равна нулю, если
. Производная будет равна нулю, если  . Обобщив полученный результат на
. Обобщив полученный результат на 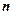 тел, получим искомое соотношение — закон сохранения импульса.
тел, получим искомое соотношение — закон сохранения импульса. ,
,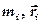 — масса и радиус - вектор
— масса и радиус - вектор 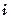 -ой точки соответственно,
-ой точки соответственно,  — масса системы.
— масса системы. под действием силы
под действием силы 
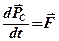 .
. — результирующая внешних сил, приложенных к системе.
— результирующая внешних сил, приложенных к системе. . Отсюда следует
. Отсюда следует  — импульс системы равен импульсу центра масс. Подставив импульс центра масс
— импульс системы равен импульсу центра масс. Подставив импульс центра масс 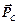 в основной закон динамики, получим искомое соотношение — закон движения центра масс.
в основной закон динамики, получим искомое соотношение — закон движения центра масс. — это произведение силы
— это произведение силы  её действия
её действия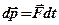 .
. ¨ Элементарная работа
¨ Элементарная работа  силы
силы  — это скалярное произведение
— это скалярное произведение  .
.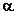 — угол (рис. 3.1) между векторами
— угол (рис. 3.1) между векторами  — проекция силы
— проекция силы  — элементарный путь, пройденный за время
— элементарный путь, пройденный за время  , то
, то  — работа силы тяги всегда положительна, если
— работа силы тяги всегда положительна, если  , то
, то  — работа сил сопротивления всегда отрицательна, если
— работа сил сопротивления всегда отрицательна, если  , то
, то  — работа центростремительных сил или сил реакции опоры равна нулю.
— работа центростремительных сил или сил реакции опоры равна нулю. на конечном участке траектории находится алгебраическим суммированием (интегрированием) элементарных работ на всем пути
на конечном участке траектории находится алгебраическим суммированием (интегрированием) элементарных работ на всем пути .
. на участке 1-2 траектории.
на участке 1-2 траектории.
 — проекция силы на направление движения,
— проекция силы на направление движения, 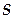 — дуговаякоордината материальной точки, отсчитываемая вдоль траектории.
— дуговаякоордината материальной точки, отсчитываемая вдоль траектории. .
. .
. , то
, то  , где
, где  — угол между векторами силы
— угол между векторами силы 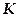 — это энергия механического движения тела (системы).
— это энергия механического движения тела (системы).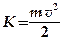 .
.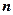 материальных точек
материальных точек ,
, — масса,
— масса,  — скорость
— скорость  .
. Доказательство. Пусть скорость тела (рис. 3.3) массой
Доказательство. Пусть скорость тела (рис. 3.3) массой  под действием силы
под действием силы  до
до  . Найдем работу
. Найдем работу 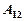 силы
силы  . Т.к.
. Т.к. 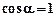 (рис. 3.3) и
(рис. 3.3) и  , то
, то  . Учитывая, что ускорение
. Учитывая, что ускорение 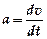 , получаем
, получаем  , или
, или .
. ,
,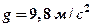 — ускорение свободного падения. Единица потенциальной энергии — джоуль (Дж).
— ускорение свободного падения. Единица потенциальной энергии — джоуль (Дж). является консервативной.
является консервативной. 
 (рис. 3.4) при перемещении тела из
(рис. 3.4) при перемещении тела из  в
в  вдоль произвольной траектории.
вдоль произвольной траектории. . Т.к.
. Т.к.  ,
, .
. и конечной
и конечной  высотой. Следовательно, сила тяжести является консервативной. Из полученного выражения следует, что работа консервативных сил по замкнутой траектории равна нулю.
высотой. Следовательно, сила тяжести является консервативной. Из полученного выражения следует, что работа консервативных сил по замкнутой траектории равна нулю.
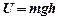 , то соотношение предыдущего пункта принимает вид
, то соотношение предыдущего пункта принимает вид  . Или
. Или  . Знак минус указывает на то, что потенциальная энергия уменьшается.
. Знак минус указывает на то, что потенциальная энергия уменьшается. .
.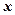 . По определению работа
. По определению работа  . С другой стороны
. С другой стороны  . Из указанных соотношений следует
. Из указанных соотношений следует  — консервативная сила равна градиенту потенциальной энергии с обратным знаком (градиент — скорость изменения потенциальной энергии в пространстве).
— консервативная сила равна градиенту потенциальной энергии с обратным знаком (градиент — скорость изменения потенциальной энергии в пространстве).
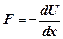 , то
, то 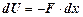 . По закону Гука
. По закону Гука  , тогда
, тогда 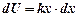 . Интегрируя полученное соотношение, найдем потенциальную энергию пружины с учетом изменения ее длины от
. Интегрируя полученное соотношение, найдем потенциальную энергию пружины с учетом изменения ее длины от 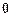 до
до  :
:  . Здесь
. Здесь  — жесткость,
— жесткость,  : полная энергия системы, в которой действуют только консервативные силы, не меняется с течением времени
: полная энергия системы, в которой действуют только консервативные силы, не меняется с течением времени .
. — это кинетическая энергия, и
— это кинетическая энергия, и 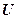 — потенциальная энергия всех тел системы соответственно.
— потенциальная энергия всех тел системы соответственно. . Согласно теореме о кинетической энергии
. Согласно теореме о кинетической энергии  . Из представленных соотношений следует
. Из представленных соотношений следует 
 . Т.к. изменение
. Т.к. изменение  равно нулю, то полная энергия механической системы сохраняется.
равно нулю, то полная энергия механической системы сохраняется. Шар массой
Шар массой  , двигаясь (рис. 3.5) вдоль оси
, двигаясь (рис. 3.5) вдоль оси 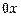 со скоростью
со скоростью  , налетает на покоящийся шар массой
, налетает на покоящийся шар массой 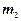 . Найдем скорости
. Найдем скорости  и
и 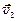 шаров после удара.
шаров после удара. ,
, .
. и
и  указанные выражения, получим
указанные выражения, получим (1),
(1), (2).
(2). и подставим в (2):
и подставим в (2):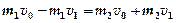 .
. .
. . Подставим
. Подставим  в (2)
в (2)

 одинаковы, то после столкновения первый шар остановится
одинаковы, то после столкновения первый шар остановится  , а второй будет двигаться со скоростью
, а второй будет двигаться со скоростью  .
. (столкновение со стенкой), то после удара первый шар будет двигаться в противоположном направлении со скоростью
(столкновение со стенкой), то после удара первый шар будет двигаться в противоположном направлении со скоростью  , а скорость второго останется без изменения
, а скорость второго останется без изменения  .
. .
. Шар массой
Шар массой  , налетает на покоящийся шар массой
, налетает на покоящийся шар массой 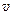 шаров после удара. Согласно закону сохранения импульса
шаров после удара. Согласно закону сохранения импульса  . Отсюда следует
. Отсюда следует .
. .
. , то
, то  , а кинетическая энергия налетающего тела переходит во внутреннюю энергию.
, а кинетическая энергия налетающего тела переходит во внутреннюю энергию. ¨ Задача 5. На материальную точку (мт) массой
¨ Задача 5. На материальную точку (мт) массой  кг действуют две консервативные силы
кг действуют две консервативные силы  Н, и
Н, и  Н (рис. 3.7). Начальная скорость
Н (рис. 3.7). Начальная скорость  м/с мт направлена по результирующей силе. Время
м/с мт направлена по результирующей силе. Время  ,
,  с.
с.
 (рис. 3.8). Для этого используем теорему Пифагора:
(рис. 3.8). Для этого используем теорему Пифагора: (Н).
(Н). , полагая при этом, что в начальный момент времени
, полагая при этом, что в начальный момент времени  (рис. 3.8).
(рис. 3.8).
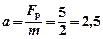 (м/с2).
(м/с2). и
и  .
. а координата по зависимости
а координата по зависимости  где
где  (м/с2) — ускорение и
(м/с2) — ускорение и  (м/с);
(м/с);  (м).
(м). . В начальный момент времени
. В начальный момент времени  (кг×м/с), в момент времени
(кг×м/с), в момент времени 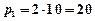 (кг×м/с). По основному закону динамики:
(кг×м/с). По основному закону динамики: 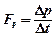 . Или
. Или  (Н), что совпадает с данными задачи.
(Н), что совпадает с данными задачи. результирующей силы в интервале времени
результирующей силы в интервале времени  по формуле механической работы.
по формуле механической работы. . В данном случае
. В данном случае  Н; перемещение
Н; перемещение  за время
за время  (с) определяется как
(с) определяется как  (м); угол между силой и перемещением (скоростью)
(м); угол между силой и перемещением (скоростью) 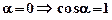 . В итоге получаем:
. В итоге получаем:  (Дж).
(Дж). и
и  в моменты времени
в моменты времени  . В момент времени
. В момент времени  (Дж), в момент времени
(Дж), в момент времени  с:
с:  (Дж).
(Дж). результирующей силы в заданном интервале времени
результирующей силы в заданном интервале времени  (Дж), что совпадает с результатами задания 4.
(Дж), что совпадает с результатами задания 4. и
и  в моменты времени
в моменты времени 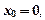 полагая
полагая  . Работа консервативных сил совершается за счет уменьшения потенциальной энергии
. Работа консервативных сил совершается за счет уменьшения потенциальной энергии 
 в данном случае
в данном случае  . В результате получаем:
. В результате получаем:  (Дж).
(Дж). Проверить выполнение закона сохранения механической энергии.
Проверить выполнение закона сохранения механической энергии. — это сумма кинетической и потенциальной энергии, поэтому: в момент времени
— это сумма кинетической и потенциальной энергии, поэтому: в момент времени 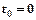 :
:  (Дж);
(Дж); с:
с:  (Дж).
(Дж).


