
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скінчені різниці. Інтерполяційні формули Ньютона для рівновіддалених вузлівСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Якщо вузли інтерполяції рівновіддалені: х0, х1 = х0 + h, х2 = х0 + 2h, …, хn = х0 + nh, то інтерполяційна формула Ньютона спрощується, а алгоритми для деяких задач стають ефективнішими. Замість поділених різниць в таких випадках використовують так звані скінчені різниці. Означення 7. Нехай функція у = f (x) задана в точках хk = х0 + kh, де h – дійсна стала, k = 0,1,…,n, yk = f (хk). Тоді величину Δуi = Δ f i = f (хi+1) – f (хi) називають скінченими різницями першого порядку. Скінчені різниці другого порядку Δ2уi – це різниці перших різниць, тобто Δ2уi = Δ2 f i = Δ f i +1 – Δ f i = f (хi+2) – 2 f (хi+1) + f (хi). За індукцією різниці Δnуi порядку n – це різниці різниць порядку n – 1: Δnуi = Δn f i = Δn-1 f i +1 – Δn-1 f i. Зазначимо, що нижні індекси при Δnуi завжди ті ж самі, що у від’ємника Δn-1 f i. Можна довести по індукції, що Δnуk = уk+n – nуk+n-1 + Лема 2. Якщо хk = х0 + kh, то виконується рівність: f (xk; xk+1;…; xk+n) = Доведення проведемо по індукції. При n = 1 маємо f (xk; xk+1) = f (xk; xk+1;…; xk+ l +1) = Отже, рівність виконується і при n = l + 1. Лему доведено. Наслідок. Якщо f = Рm – многочлен степеня m, то Δnуk = Справді, за теоремою 2 пункт 4, якщо функція f (x) n + 1 раз неперервно диференційовна, то f (x0; x1;…; xn) = Зворотно, якщо для деякого n Δnуk ≈ 0 при всіх k, то f (xk; xk+1;…; xk+n) ≈ 0 і отже Теорема 3. Нехай вузли інтерполяції хk = х0 + kh, де h – дійсна стала, k = 0,1,…,n, yk = f (хk). Тоді інтерполяційна формула Ньютона набуває вигляду:
f (x) ≈ Ln(x) = y0 + tΔу0 + де t = (х – x0)/h. Якщо функція f (x) n + 1 раз неперервно диференційовна, то залишковий член (абсолютна похибка інтерполяції) Rn(f,x) = f (x) – Ln(x) дорівнює Rn(f,x) = Доведення. Згідно з теоремою 2 пункт 3 Ln(x) = f (x0) + f (x0; x1)(х – х0) + … + f (x0; x1;…; xn)(х – x0)(х – x1) … (х – хn-1). Згідно з лемою 2 для вузлів хk = х0 + kh виконується рівність: f (x0; x1;…; xk) = Означення 8. Інтерполяційну формулу f (x) ≈ Ln(x) = y0 + tΔу0 + де t = (х – x0)/h, називають першою інтерполяційною формулою Ньютона. Зокрема при n = 1 маємо формулу лінійної інтерполяції f (x) ≈ f (x0) + Згідно з формулою для абсолютної похибки інтерполяції │Rn(f,x)│ набуває найменше можливе значення за умови, що найменші можливі значення мають відстані │xi – х│ від х до вузлів інтерполяції xi. Для цього необхідно, щоби вони були занумеровані в порядку зростання │xi – х│ (як і в схемі Ейткіна). Насправді в умовах теореми 3 це буде виконано, якщо х міститься на початку таблиці, тобто х є [x0; x1]. Якщо х є [x1; x2], то користуватись безпосередньо формулою (3) недоцільно, бо t буде більшим за 1. У цьому разі за перший вузол треба взяти x1 і в інтерполяційному многочлені використовувати скінчені різниці Δу1, Δ2у1, …, Δnу1. Тому першу інтерполяційну формулу Ньютона називають також формулою Ньютона для інтерполювання вперед. Якщо значення х лежить ближче до кінця відрізкаінтерполювання, то вузли треба занумерувати у зворотному порядку: xn, xn-1, …, x1, x0. Звідси так само, як у теоремі 3, отримаємо Ln(x) = f (xn) + f (xn; xn-1) ∙ (х – хn) + … + f (xn; xn-1;…; x0)(х – хn-1) … (х – x1)(х – x0) = yn + tΔуn-1 +
Означення 9. Інтерполяційну формулу f (x) ≈ Ln(x) = yn + tΔуn-1 + де t = (х – хn)/h, називають другою інтерполяційною формулою Ньютона або формулою Ньютона для інтерполювання назад. При такій нумерації відповідна формула залишкового члена має вигляд Rn(f, x) =
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 486; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.149.71 (0.011 с.) |

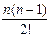 уk+n-2 – … + (– 1)nуk =
уk+n-2 – … + (– 1)nуk = 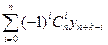 . Ця формула нагадує розклад за формулою бінома Ньютона: коефіцієнт при уk+n-m у цій формулі дорівнює коефіцієнту при ym у розкладі (у – 1)n за формулою бінома. Скінчені різниці просто зв’язані з поділеними різницями.
. Ця формула нагадує розклад за формулою бінома Ньютона: коефіцієнт при уk+n-m у цій формулі дорівнює коефіцієнту при ym у розкладі (у – 1)n за формулою бінома. Скінчені різниці просто зв’язані з поділеними різницями. .
. =
=  . Припустимо, що рівність виконується при всіх степенях поділених різниць n = 1, …, l. Звідси маємо
. Припустимо, що рівність виконується при всіх степенях поділених різниць n = 1, …, l. Звідси маємо =
=  =
=  .
. , де с – деяка стала (незалежна від k).
, де с – деяка стала (незалежна від k).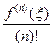 , де min{x0; x1;…; xn} ≤ ξ ≤ max{x0; x1;…; xn}. Звідси, якщо у якості f (x) взяти деякий многочлен Pm(x) степеня m ≤ n, то Pm(xk;…;xk+n) =
, де min{x0; x1;…; xn} ≤ ξ ≤ max{x0; x1;…; xn}. Звідси, якщо у якості f (x) взяти деякий многочлен Pm(x) степеня m ≤ n, то Pm(xk;…;xk+n) =  , де b – це коефіцієнт многочлена Pm(x) при хm. Згідно з лемою 2, якщо хk = х0 + kh, то Pm(xk; xk+1;…; xk+n) =
, де b – це коефіцієнт многочлена Pm(x) при хm. Згідно з лемою 2, якщо хk = х0 + kh, то Pm(xk; xk+1;…; xk+n) = 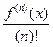 ≈ 0 при всіх х на відрізку min{x0; x1;…; xn} ≤ х ≤ max{x0; x1;…; xn}. Отже, з деякою прийнятною похибкою можна вважати, що на цьому відрізку f (x) ≈ Pm(x), де Pm(x) – деякий многочлен степеня m < n і отже за означенням це інтерполяційний многочлен.
≈ 0 при всіх х на відрізку min{x0; x1;…; xn} ≤ х ≤ max{x0; x1;…; xn}. Отже, з деякою прийнятною похибкою можна вважати, що на цьому відрізку f (x) ≈ Pm(x), де Pm(x) – деякий многочлен степеня m < n і отже за означенням це інтерполяційний многочлен. Δ2у0 + … +
Δ2у0 + … +  Δnу0,
Δnу0, hn+1t(t –1)(t – 2)…(t – n) ≈
hn+1t(t –1)(t – 2)…(t – n) ≈  t(t – 1)(t – 2)…(t – n) (х0 ≤ ξ ≤ хn).
t(t – 1)(t – 2)…(t – n) (х0 ≤ ξ ≤ хn). . Нарешті очевидно, що х – xk = x – х0 – kh = h(
. Нарешті очевидно, що х – xk = x – х0 – kh = h( – k) = h(t – k), звідки (х – x0)(х – x1) … (х – хk-1) = hkt(t – 1)(t – 2)…(t – k + 1). Отже, f (x0; x1;…; xk)(х – x0)(х – x1) … (х – хk-1) =
– k) = h(t – k), звідки (х – x0)(х – x1) … (х – хk-1) = hkt(t – 1)(t – 2)…(t – k + 1). Отже, f (x0; x1;…; xk)(х – x0)(х – x1) … (х – хk-1) = 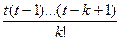 Δkу0, що і доводить інтерполяційну формулу. Якщо функція f (x) n + 1 раз неперервно диференційовна, то згідно з теоремою 1 Rn(f,x) =
Δkу0, що і доводить інтерполяційну формулу. Якщо функція f (x) n + 1 раз неперервно диференційовна, то згідно з теоремою 1 Rn(f,x) =  ≈ f (x0; x1;…; xn+1) =
≈ f (x0; x1;…; xn+1) =  . Отже, Rn(f,x) =
. Отже, Rn(f,x) =  (x – x0), яка була використана у розділі 2. Тут R1(f,x) ≈
(x – x0), яка була використана у розділі 2. Тут R1(f,x) ≈  t(t – 1). При n = 2 маємо формулу квадратичної інтерполяції f (x) ≈ у0 +
t(t – 1). При n = 2 маємо формулу квадратичної інтерполяції f (x) ≈ у0 +  (х – x0) +
(х – x0) +  (х – x0)(х – x1), R2(f,x) ≈
(х – x0)(х – x1), R2(f,x) ≈  t(t – 1)(t – 2).
t(t – 1)(t – 2). Δ2уn-2 + … +
Δ2уn-2 + … + 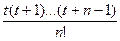 Δnу0.
Δnу0.


