
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Опис експериментальної установки та вивід робочої формулиСодержание книги
Поиск на нашем сайте
Під час виконання цієї лабораторної роботи вимірюється ширина a певної кількості k інтерференційних смуг за допомогою окулярного мікрометра. Тоді ширину смуги у цьому випадку можна визначити за формулою
де S – віддаль від лінзи до предмета (щілини);
Установка, для визначення довжини хвилі схематично зображена на рис.3. На цьому рисунку: 1 – оптична лава; 2 – джерело світла; 3 – щілина; 4 – біпризма Френеля; 5 – окулярний мікрометр; б – додатковий рейтер для установки лінзи. Хід роботи 1. Ввімкнути живлення джерела світла. Регулюючи його положення, добитися, щоб промінь потрапляв на щілину. 2. Регулюючи ширину щілини і положення окулярного мікрометра, добитися чіткої інтерференційної картини. 3. Відрахувати якомога більше число k інтерференційних смуг. Користуючись окулярним мікрометром, визначити координати а 1 та а 2 крайніх смуг. Дослід для визначення а 1 та а 2 повторити кілька разів. 4. Закріпити на оптичній лаві між біпризмою і окулярним мікрометром збиральну лінзу. 5. Відрегулювати положення лінзи так, щоб чітко було видно зображення обох джерел. У цьому положенні виміряти віддаль між лінзою і щілиною S і лінзою та площиною окулярного мікрометра 6. Заміряти координати зображень джерел c 1 та c 2. 7. Зміщуючи лінзу, знову виконати пункти 5 та 6, вимірюючи кілька разів значення величин S, 8. Виміряти за допомогою лінійки віддаль L між щілиною і площиною окулярного мікрометра. Таблиця вимірювань
Обробка результатів вимірювань 1. Для кожного виміру визначити 2. За формулою (4) знайти довжину хвилі світла λ. 3. Обчислити відносну та абсолютну похибки експерименту за формулами (5) і записати кінцевий результат.
Контрольні запитання Які хвилі називаються когерентними? 1. Які є способи отримання когерентних світлових пучків? 2. Що таке інтерференція? 3. Записати і пояснити умови максимуму і мінімуму інтерференції світла. 4. Який вигляд має інтерференційна картина від двох точкових когерентних джерел на плоскому екрані? Записати і пояснити умови максимуму і мінімуму для цього випадку. 5. Нарисувати хід променів у призмі. У якому випадку призма створює уявне зображення точкового, джерела світла і де воно знаходиться? 6. Як у даній роботі знаходиться віддаль між уявними джерелами світла? 7. Вивести робочу формулу. Лабораторна робота № 5.2 Визначення радіуса кривизни лінзи за допомогою кілець Ньютона Мета роботи: дослідити інтерференцію світла на сферичному клині і визначити радіус кривизни лінзи. Теоретичні відомості (теорію до даної роботи див. також у конспекті лекцій, §§6.2-6.4) Одним із найцікавіших випадків інтерференції світла є так звані кільця Ньютона. Якщо на плоску скляну пластинку Е (рис. 1) покласти опуклим боком плоско-опуклу лінзу L з дуже великим радіусом кривизни R (кілька метрів), то, при освітленні монохроматичним (одноколірним) світлом, починаючи від місця стикання лінзи зі скляною пластинкою, спостерігається декілька концентричних темних і світлих кілець або, при освітлені білим світлом, райдужних кілець. Ці кільця дістали назву кілець Ньютона. Кільця Ньютона утворюють геометричні місця точок, в яких різниця ходу когерентних світлових променів стала внаслідок сталої товщини середовища (тому їх називають смугами однакової товщини). Зазначене явище є результатом інтерференції когерентних променів на дуже тонкому повітряному прошарку, товщина якого d поступово збільшується від місця дотику. Цей прошарок утворюється між кривою поверхнею лінзи і плоскою поверхнею пластинки. Кільця Ньютона можна спостерігати як у відбитому, так і в прохідному світлі. У першому випадку у центрі кілець буде темна пляма, а в другому – світла. Кільця у відбитому світлі видно краще, ніж в прохідному.
де d – товщина повітряного прошарку в певному місці. Доданок Як відомо, умови мінімумів та максимумів інтерференції когерентних променів математично виражаються так:
де т – ціле число, котре в цьому випадку визначає порядковий номер кільця. Згідно трьох останніх формул умова виникнення темних кілець матиме вигляд:
Величина d може бути виражена за теоремою Піфагора через радіус кривизни лінзи R і радіус темного інтерференційного кільця
Якщо d мале порівняно з R,то
З рівнянь (1) та (2) слідує, що
З формули (3) видно, що залежність
де α – коефіцієнт пропорційності, що має розмірність площі. З формул (3) і (4) визначимо радіус кривизни лінзи:
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.247.221 (0.01 с.) |

 Можна показати, що ширина інтерференційної смуги від двох точкових когерентних джерел дорівнює
Можна показати, що ширина інтерференційної смуги від двох точкових когерентних джерел дорівнює (1)
(1)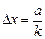 (2)
(2)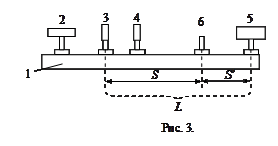 Віддаль між уявними джерелами світла d безпосередньо виміряти не можна. Для її знаходження між біпризмою і площиною екрана (площиною окулярного мікрометра) розміщується збиральна лінза. Її положення підбирається таким чином, щоб в окулярному мікрометрі було видно зображення уявних джерел (у вигляді двох чітких світлих ліній). Вимірюється віддаль c між зображеннями джерел. Згідно формули лінійного збільшення лінзи отримаємо
Віддаль між уявними джерелами світла d безпосередньо виміряти не можна. Для її знаходження між біпризмою і площиною екрана (площиною окулярного мікрометра) розміщується збиральна лінза. Її положення підбирається таким чином, щоб в окулярному мікрометрі було видно зображення уявних джерел (у вигляді двох чітких світлих ліній). Вимірюється віддаль c між зображеннями джерел. Згідно формули лінійного збільшення лінзи отримаємо . (3)
. (3) – віддаль від лінзи до зображення (площини окулярного мікрометра). З формул (1), (2) та (3) знаходимо вираз для довжини світлової хвилі
– віддаль від лінзи до зображення (площини окулярного мікрометра). З формул (1), (2) та (3) знаходимо вираз для довжини світлової хвилі . (4)
. (4) , c 1, c 2.
, c 1, c 2.

 ,
,  Знайти середні значення величин а, с, S,
Знайти середні значення величин а, с, S,  ,
,  (5)
(5) На рис.1 зображено утворення двох когерентних променів
На рис.1 зображено утворення двох когерентних променів  та
та  з одного променя 1. Оскільки, між лінзою L і пластинкою Е знаходиться повітря (
з одного променя 1. Оскільки, між лінзою L і пластинкою Е знаходиться повітря ( ) і пучок світла падає нормально до пластинки та практично до нижньої поверхні лінзи (кривизна лінзи мала), то оптична різниця ходу Δ світлових променів
) і пучок світла падає нормально до пластинки та практично до нижньої поверхні лінзи (кривизна лінзи мала), то оптична різниця ходу Δ світлових променів  ,
, в останній формулі виникає тому, що під час відбивання хвилі від межі середовища з більшим показником заломлення її фаза змінюється на π.
в останній формулі виникає тому, що під час відбивання хвилі від межі середовища з більшим показником заломлення її фаза змінюється на π.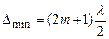 ,
,  ,
, . (1)
. (1) . З рис. 1 знаходимо, що
. З рис. 1 знаходимо, що .
.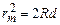 . (2)
. (2) . (3)
. (3) від номера кільця т лінійна, тобто може бути представлена у вигляді
від номера кільця т лінійна, тобто може бути представлена у вигляді , (4)
, (4) . (5)
. (5)


