
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнетизм. Коливання і хвиліСодержание книги Поиск на нашем сайте ІV. Лабораторний практикум Магнетизм. Коливання і хвилі Лабораторна робота № 4.1 Вивчення гальванометра магнітоелектричної системи Мета роботи: визначити внутрішній опір гальванометра, ціну поділки по струму і по напрузі. Теоретичні відомості (теорію до даної роботи див. також у конспекті лекцій, §§3.10-3.11, 4.1) Гальванометр магнітоелектричної системи служить для вимірювання малих постійних струмів і напруг Контур зі струмом характеризується магнітним моментом
де Згідно з законом Ома, спад напруги на гальванометрі
де
де
ціна поділки гальванометра по напрузі. Для визначення Згідно закону Ома, сила струму на ділянці АС
Підставляючи вираз (8) у формулу (7), одержимо
звідки
Очевидно, що
В загальному випадку зі зміною Спад напруги на дільниці АВ дорівнює
де За законом Кірхгофа
Розв’язуючи систему рівнянь (9), (11) і (12) відносно
Нехай
де
Із формули (13)
а з виразу (14)
Прирівнюючи праві частини одержаних виразів і в (16) і (17), маємо
Підставляючи значення
Ціну поділки по струму визначаємо із рівняння (14)
Хід роботи
2. Замкнути ключ К і підібрати опір 3. Підібрати опір 4. Провести ще два таких досліди при незмінних опорах 5. Знайти 6. Записати покази вольтметра. 7. Обчислити похибки прямих вимірювань для величин 8. Користуючись формулами 19, 20 і 6, обчислити 9. Обчислити абсолютну та відносну похибки вимірювання
10. Записати кінцевий результат.
Таблиця вимірювань
Контрольні запитання 1. Що називається магнітним моментом контура зі струмом? Які його величина, напрямок, одиниця? 2. Записати вираз для момента сили, що діє на контур зі струмом, вміщений в магнітне поле. 3. При якій орієнтації контура зі струмом в магнітному полі обертаючий момент максимальний? В якому випадку він дорівнює нулю? 4. Яка будова і принцип дії гальванометра магнітоелектричної системи? 5. Дайте визначення ціни поділки гальванометра по струму і по напрузі. Встановіть зв’язок між 6. Покажіть, що кут повороту рухомої частини гальванометра прямо пропорційний силі струму. 7. Чи можна гальванометром магнітоелектричної системи вимірювати змінні струми? Відповідь обґрунтуйте. Лабораторна робота № 4.2 Перевірка закону Ампера Мета роботи: перевірити закон Ампера; обчислити індукцію магнітного поля. Опис установки
Теоретичні відомості (теорію до даної роботи див. також у конспекті лекцій, §§4.1, 4.4, 5.1, 5.3) Нехай у магнітному полі з індукцією
або у скалярній формі
де Сила, що діє на провідник зі струмом скінченої довжини, знаходиться з (1) або (2) інтегруванням по всій довжині провідника
Напрямок сили Ампера знаходиться за правилом лівої руки (рис.2). Щоб одержати формулу для обчислення сили Ампера в даній лабораторній роботі, розглянемо рівняння руху фізичного маятника (рамки abcd) Цей маятник здійснює коливання відносно осі cd. Застосуємо до нього основний закон динаміки обертального руху твердого тіла
де
де Якщо через провідник ab, що знаходиться в магнітному полі електромагніта М, проходить електричний струм, то на маятник, крім сили тяжіння, діє сила Ампера. Напрямок сили Ампера, в залежності від напрямку струму, або співпадає з напрямком сили тяжіння, або протилежний до нього. Сила Ампера прикладена до провідника ab і створює момент сили
де Після підстановки (7) і (6) в (5) одержимо
Для малих кутів
Введемо позначення
тоді останнє рівняння набуде вигляду
Вираз (9) – диференціальне рівняння вільних гармонічних коливань, розв’язок котрого
де
З (8) і (11) знайдемо
Циклічна чистота пов’язана з періодом коливань співвідношенням
де
де
де В даній лабораторній роботі індукція магнітного поля В залишається незмінною, тому залежність
Хід роботи 1. Скласти електричне коло за схемою рис.1. 2. Виміряти час заданої викладачем кількості коливань маятника як без струму ( 3. Обчислити за формулою (13) силу Ампера для кожного значення сили струму; результати записати в таблицю 1. 4. Побудувати графік залежності 5. Визначити середнє значення В.
Таблиці вимірювань Таблиця 1 с =.
Таблиця 2
Контрольні запитання 1. Сформулювати і записати закон Ампера. Як визначається напрямок сили Ампера? 2. При якій орієнтації провідника зі струмом у магнітному полі сила Ампера максимальна? 3. Дати визначення вектора магнітної індукції, вказати його одиницю в СІ. 4. Які коливання називаються вільними, гармонічними? Записати диференціальне рівняння вільних гармонічних коливань та його розв’язок. 5. Дати визначення основних характеристик гармонічних коливань (амплітуди, частоти, періода, циклічної частоти, фази). Встановити зв’язок між циклічною частотою і періодом. 6. Що таке фізичний маятник? Вивести диференціальне рівняння вільних гармонічних коливань фізичного маятника. Чи будуть коливання маятника гармонічними при великих амплітудах? 7. Як впливає сила Ампера на період коливань фізичного маятника в даній лабораторній роботі? Як зміниться період коливань маятника при зміні напрямку струму на протилежний? 8. Вивести робочу формулу для обчислення сили Ампера. Чому при її виведенні не враховують індукційні струми? Лабораторна робота № 4.3 Визначення питомого заряду електрона методом магнетрона Мета роботи: виміряти питомий заряд електрона методом магнетрона. Теоретичні відомості (теорію до даної роботи див. також у конспекті лекцій, §§3.17, 4.5) Найпростіший магнетрон – це вакуумний діод, що знаходиться в однорідному магнітному полі соленоїда, індукція котрого напрямлена вздовж осі системи. Діод складається з циліндричного порожнистого анода радіуса R і катода у вигляді дротини малого радіуса. Катод розміщений вздовж осі циліндричного анода. Електрони, що вилітають з розжареного катода під дією електричного поля, створеного між анодом і катодом, прямують до анода. При цьому силами поля виконується робота
де U – різниця потенціалів між анодом і катодом, е – елементарний заряд. За рахунок цієї роботи збільшується кінетична енергія електрона. Тому маємо
де
При наявності магнітного поля, вектор індукції котрого напрямлений вздовж осі катода, на електрон крім електричного поля буде діяти сила Лоренца, що перпендикулярна до вектора швидкості електрона
Оскільки
Якби швидкість електрона була постійною за величиною, то величина сили Лоренца також була б постійною. Електрон рухався б по колу (сила Лоренца при цьому виконує роль доцентрової сили). Маємо
Звідси знаходимо радіус кола, по якому рухається електрон
Однак, величина швидкості електрона не постійна, тому електрон описує не коло, а більш складну криву. В лампі з катодом і анодом у вигляді коаксіальних циліндрів, коли радіус катода набагато менший радіуса анода, найбільша напруженість електричного поля біля самого катода. Внаслідок цього швидкість електрона суттєво змінюється біля самого катода, а далі є величиною майже постійною. Тому наближено можна вважати, що електрон у магнетроні рухається по колу. З виразу (7) видно, що чим більша індукція магнітного поля В, тим менший радіус кривизни траєкторії електронів. При деякому критичному значенні індукції магнітного поля Вк електрони, не долітаючи до анода, починають рухатися по колу радіусом
Із співвідношення (3) і (7) та з врахуванням, що
Індукція магнітного поля соленоїда, довжина
де Остаточно, підставляючи (9) у (8), маємо
Співвідношення (10) є робочою формулою для визначення питомого заряду. Таблиця вимірювань U =, l =, d =, R =, N=, μ0=, Iск= Δ U 0=, Δ l 0=, Δd0=, ΔR0=, ΔN0=, Δ(μ0)0=, Δ(Iск)0=
Контрольні запитання 1. Яка будова магнетрона? Практичне використання магнетрона. 2. Описати електромагнітне поле в магнетроні. 3. Довести, що сила Лоренца не виконує роботи. 4. При яких умовах виникає сила Лоренца? Яка величина і напрям сили Лоренца? 5. Чому в залежності 6. Вивести робочу формулу. Лабораторна робота № 4.4 Вивчення магнітного поля соленоїда за допомогою датчика Холла Мета роботи: ознайомитися з холлівським методом вимірювання індукції магнітного поля; дослідити залежність індукції магнітного поля в центрі соленоїда від струму; дослідити осьову неоднорідність магнітного поля в соленоїді. Теоретичні відомості (теорію до даної роботи див. також у конспекті лекцій, §§4.2-4.3)
де
Тут враховано, що для усякого елементу
Зауважимо, що в центрі колового струму (
Врахувавши, що
Якщо соленоїд дуже довгий
Зауважимо, що формулу (6) можна отримати, використавши теорему про циркуляцію вектора індукції магнітного поля. Для дуже довгого соленоїда магнітне поле практично однорідне (силові лінії еквідистантні і паралельні до осі соленоїда). Для реальних соленоїдів, коли нерівність
Ця сила, як видно з рис.4, буде відхиляти носії до грані 1, і між гранями 1 та 2 виникне поперечне холлівське поле з напруженістю
Різниця потенціалів між гранями 1, 2 або холлівська напруга складає
Якщо врахувати, що густина струму пов’язана з
де І – сила струму через кристал, а
Отже, для визначення значення індукції магнітного поля соленоїда достатньо виміряти холлівську напругу між контактами 1–2 ДХ (рис.5) і помножити її на
де 4. Блок-схема експериментальної установки показана на рис.6. Блок живлення забезпечує регульований (регулятор Р) струм через соленоїд Хід роботи Завдання 1. Дослідження залежності магнітної індукції в центрі соленоїда від струму соленоїда.
2. Розмістити шток з ДХ в трубі соленоїда в положенні “0” по шкалі (центр соленоїда). 3. Ввімкнути в мережу ~220В БЖ і ЦВ, поставивши перемикач К в положення 4. Виміряти напругу 5. За формулою (12) розрахувати 6. Побудувати графік залежності | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

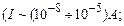
 . В основі роботи гальванометра лежить дія магнітного поля на рамку з електричним струмом.
. В основі роботи гальванометра лежить дія магнітного поля на рамку з електричним струмом. , (1)
, (1)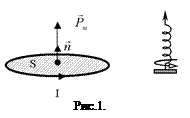 де
де  – сила струму,
– сила струму,  – площа контура,
– площа контура,  – одиничний вектор нормалі до площини контура, зв’язаний з напрямком струму правилом правого гвинта (рис.1). Якщо контур зі струмом вмістити в магнітне поле, то на нього діятиме обертаючий момент сили
– одиничний вектор нормалі до площини контура, зв’язаний з напрямком струму правилом правого гвинта (рис.1). Якщо контур зі струмом вмістити в магнітне поле, то на нього діятиме обертаючий момент сили  або в скалярній формі
або в скалярній формі , (2)
, (2) де
де  – вектор магнітної індукції,
– вектор магнітної індукції, 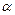 – кут між
– кут між 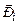 і
і  між нерухомим циліндром А, виготовленим з м’якого заліза, і полюсними башмаками
між нерухомим циліндром А, виготовленим з м’якого заліза, і полюсними башмаками  знаходиться прямокутна котушка (рамка) К. Вона укріплена на двох півосях, на одній з яких закріплена вказівна стрілка приладу. За кінцем стрілки розміщена шкала. Струм до рухомої котушки підводиться через дві спіральні пружини. У відсутності струму ці пружини утримують рамку в рівноважному положенні, коли її площина паралельна до
знаходиться прямокутна котушка (рамка) К. Вона укріплена на двох півосях, на одній з яких закріплена вказівна стрілка приладу. За кінцем стрілки розміщена шкала. Струм до рухомої котушки підводиться через дві спіральні пружини. У відсутності струму ці пружини утримують рамку в рівноважному положенні, коли її площина паралельна до 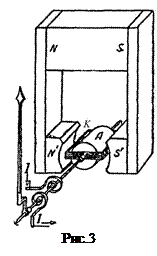
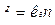 , (3)
, (3)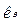 – коефіцієнт пропорціональності, який називається ціною поділки приладу по струму,
– коефіцієнт пропорціональності, який називається ціною поділки приладу по струму, 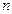 – кількість поділок, на яку відхилилась стрілка при вимірюванні. З (3) знайдемо
– кількість поділок, на яку відхилилась стрілка при вимірюванні. З (3) знайдемо 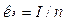 , тобто ціна поділки гальванометра по струму дорівнює силі струму, який викликає зміщення стрілки приладу на одну поділку.
, тобто ціна поділки гальванометра по струму дорівнює силі струму, який викликає зміщення стрілки приладу на одну поділку. , (4)
, (4) – внутрішній опір гальванометра. З формули (3) і (4) одержимо
– внутрішній опір гальванометра. З формули (3) і (4) одержимо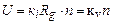 , (5)
, (5)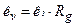 (6)
(6) ,
,  та
та  використаємо схему, подану на рис.4. Тут
використаємо схему, подану на рис.4. Тут  – досліджуваний гальванометр,
– досліджуваний гальванометр,  – вольтметр,
– вольтметр, 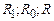 ; – магазини опорів.
; – магазини опорів. , (7)
, (7) де
де 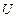 – напруга на клемах джерела,
– напруга на клемах джерела, 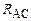 – опір дільниці кола, який рівний
– опір дільниці кола, який рівний . (8)
. (8) (9)
(9) .
. . (10)
. (10) змінюється
змінюється  і сила струму
і сила струму  , (11)
, (11) – сила струму, що проходить через гальванометр,
– сила струму, що проходить через гальванометр, 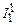 – сила струму, що проходить через опір
– сила струму, що проходить через опір 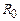 .
. . (12)
. (12) . (13)
. (13)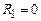 . Тоді струм, згідно з (13)
. Тоді струм, згідно з (13) , (14)
, (14) . (15)
. (15) , (16)
, (16)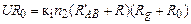 . (17)
. (17)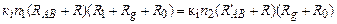 . (18)
. (18) із (10) та (15) в (18) і розв’язуючи одержане рівняння відносно
із (10) та (15) в (18) і розв’язуючи одержане рівняння відносно  . (19)
. (19) . (20)
. (20) 1. Скласти електричну схему подану на рис.5, де
1. Скласти електричну схему подану на рис.5, де  – джерело постійного струму,
– джерело постійного струму,  – гальванометр,
– гальванометр,  – магазини опорів,
– магазини опорів,  – перемикач, за допомогою якого змінюють напрямок струму в гальванометрі,
– перемикач, за допомогою якого змінюють напрямок струму в гальванометрі, 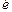 – ключ,
– ключ, 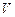 – вольтметр. Опір
– вольтметр. Опір 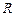 має бути великим; магазин опорів
має бути великим; магазин опорів  та
та  такий, щоб стрілка гальванометра відхилилась майже до кінця шкали. Записати показ гальванометра
такий, щоб стрілка гальванометра відхилилась майже до кінця шкали. Записати показ гальванометра 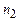 та значення опору
та значення опору  змінити напрямок струму через гальванометр і записати показ гальванометра
змінити напрямок струму через гальванометр і записати показ гальванометра 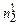 .
.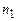 становили близько
становили близько  (в цьому випадку точність вимірювань
(в цьому випадку точність вимірювань  при двох напрямках струму.
при двох напрямках струму.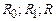 .
.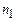 ср і
ср і  .
. .
. . (21)
. (21)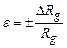 . (22)
. (22)

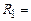
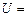


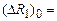
 под.
под.
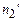
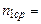
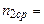
 та
та  .
.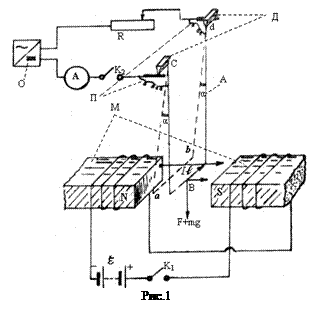 Установка для перевірки закону Ампера зображена на рис.1. Вона складається з фізичного маятника А і електромагніта М. Фізичний маятник тут – мідний провідник, зігнутий у вигляді прямокутної рамки. Сторона рамки ab довжиною
Установка для перевірки закону Ампера зображена на рис.1. Вона складається з фізичного маятника А і електромагніта М. Фізичний маятник тут – мідний провідник, зігнутий у вигляді прямокутної рамки. Сторона рамки ab довжиною  розміщена між полюсами електромагніта М перпендикулярно до ліній магнітної індукції; на протилежному до провідника ab кінці маятника закріплені опорні тригранні призми D, що опираються на спеціальні латунні підшипники. Біля опорних призм до кінців с і d припаяні легкі гнучкі провідники П, за допомогою котрих провідник ab включають в електричне коло. Струм в провіднику ab можна змінювати за допомогою реостата R і вимірювати амперметром А. Електромагніт М живиться від джерела напруги. Коло, в котре включений провідник ab, одержує напругу від джерела напруги.
розміщена між полюсами електромагніта М перпендикулярно до ліній магнітної індукції; на протилежному до провідника ab кінці маятника закріплені опорні тригранні призми D, що опираються на спеціальні латунні підшипники. Біля опорних призм до кінців с і d припаяні легкі гнучкі провідники П, за допомогою котрих провідник ab включають в електричне коло. Струм в провіднику ab можна змінювати за допомогою реостата R і вимірювати амперметром А. Електромагніт М живиться від джерела напруги. Коло, в котре включений провідник ab, одержує напругу від джерела напруги. . На нього з боку поля діє сила, величина і напрямок котрої визначаються законом Ампера
. На нього з боку поля діє сила, величина і напрямок котрої визначаються законом Ампера , (1)
, (1)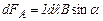 , (2)
, (2)
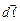 та
та 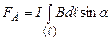 . (3)Зокрема, для прямолінійного провідника в однорідному магнітному полі
. (3)Зокрема, для прямолінійного провідника в однорідному магнітному полі 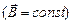 з (3) одержимо
з (3) одержимо . (4)
. (4)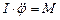 , (5)
, (5)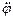 –кутове прискорення,
–кутове прискорення,  – головний момент зовнішніх сил відносно цієї осі.
– головний момент зовнішніх сил відносно цієї осі. У відсутності струму обертовий момент створює сила тяжіння (прикладена до центра мас маятника).
У відсутності струму обертовий момент створює сила тяжіння (прикладена до центра мас маятника).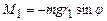 , (6)
, (6) відстань від осі обертання до центра мас,
відстань від осі обертання до центра мас,  – кут відхилення маятника від положення рівноваги,
– кут відхилення маятника від положення рівноваги, 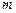 – маса маятника. Знак “–” показує, що момент сили тяжіння обертає маятник в бік, протилежний відхиленню від рівноваги.
– маса маятника. Знак “–” показує, що момент сили тяжіння обертає маятник в бік, протилежний відхиленню від рівноваги.
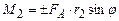 , (7)
, (7) – відстань від провідника ab до осі обертання. Знак “–” в (7) відноситься до випадку, коли сила Ампера напрямлена вниз (рис.3), а знак “+” – коли вгору (рис.4).
– відстань від провідника ab до осі обертання. Знак “–” в (7) відноситься до випадку, коли сила Ампера напрямлена вниз (рис.3), а знак “+” – коли вгору (рис.4). .
.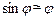 , тому, якщо кут відхилення малий, останнє рівняння можна записати у вигляді
, тому, якщо кут відхилення малий, останнє рівняння можна записати у вигляді , або
, або  .
.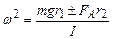 , (8)
, (8) . (9)
. (9)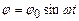 , (10)
, (10) – амплітудне значення кута відхилення,
– амплітудне значення кута відхилення, 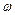 – власна циклічна частота, квадрат якої визначається рівнянням (8). Якщо струм в провіднику ab відсутній, то
– власна циклічна частота, квадрат якої визначається рівнянням (8). Якщо струм в провіднику ab відсутній, то  , і маятник коливається з циклічною частотою
, і маятник коливається з циклічною частотою 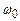 . З (8) тоді
. З (8) тоді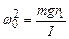 . (11)
. (11) , або
, або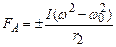 . (12)
. (12) . Врахувавши це, а також виразивши І з (11), запишемо рівняння (12) у вигляді
. Врахувавши це, а також виразивши І з (11), запишемо рівняння (12) у вигляді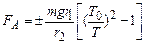 ,
, і
і  – періоди коливань маятника у відсутності та при наявності струму, відповідно. Відношення
– періоди коливань маятника у відсутності та при наявності струму, відповідно. Відношення 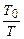 можна замінити відношенням проміжків часу
можна замінити відношенням проміжків часу  , за які маятник здійснив однакову кількість коливань. Тоді останнє рівняння набуде вигляду
, за які маятник здійснив однакову кількість коливань. Тоді останнє рівняння набуде вигляду , (13)
, (13)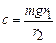 – постійна лабораторної установки, яка вказана в її паспорті. Таким чином, вимірявши
– постійна лабораторної установки, яка вказана в її паспорті. Таким чином, вимірявши  і
і 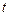 , за формулою (13) можна розрахувати силу Ампера для кількох значень сили струму і побудувати графік залежності
, за формулою (13) можна розрахувати силу Ампера для кількох значень сили струму і побудувати графік залежності 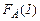 . Оскільки напрямок струму в провіднику ab перпендикулярний до ліній магнітної індукції (див. рис.1), то формула (4) для сили Ампера набуде вигляду
. Оскільки напрямок струму в провіднику ab перпендикулярний до ліній магнітної індукції (див. рис.1), то формула (4) для сили Ампера набуде вигляду , (14)
, (14)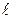 – довжина провідника ab.
– довжина провідника ab. має бути пропорційною. В цьому суть перевірки закона Ампера. Визначивши
має бути пропорційною. В цьому суть перевірки закона Ампера. Визначивши  для даного значення сили струму, з (14) можна визначити індукцію магнітного поля
для даного значення сили струму, з (14) можна визначити індукцію магнітного поля . (15)
. (15) розімкнений), так і при вказаних значеннях сили струму (
розімкнений), так і при вказаних значеннях сили струму ( замкнений). Результати вимірювань записати в таблицю Увага! Ключ К, має бути замкненим як при вимірюванні часу t, так і
замкнений). Результати вимірювань записати в таблицю Увага! Ключ К, має бути замкненим як при вимірюванні часу t, так і  – щоб виключити вплив струмів Фуко.
– щоб виключити вплив струмів Фуко.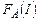 ; вибрати з графіка три експериментальні точки, які лежать на графіку або щонайменше віддалені від нього. Для цих точок порахувати за формулою (15) індукцію магнітного поля. Результати записати в таблицю 2.
; вибрати з графіка три експериментальні точки, які лежать на графіку або щонайменше віддалені від нього. Для цих точок порахувати за формулою (15) індукцію магнітного поля. Результати записати в таблицю 2.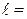 .
. , (1)
, (1)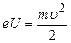 , (2)
, (2)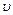 – його швидкість. З (2) знайдемо швидкість
– його швидкість. З (2) знайдемо швидкість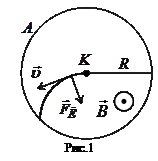
 . (3)
. (3)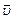 і вектора індукції магнітного поля
і вектора індукції магнітного поля 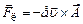 . (4)
. (4)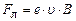 . (5)
. (5) . (6)
. (6)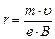 . (7)
. (7) . При цьому сила анодного струму Іа повинна різко зменшуватися (рис.2). Дослід показує, що при критичному значенні індукції магнітного поля анодний струм не падає стрибком до нуля, а плавно зменшується (рис.3). Такий хід залежності анодного струму частково пояснюється тим, що електрон, який вилетів з катода, вже має деяку швидкість. Величина її визначається тепловим рухом електронів всередині катода. Щоб зменшити вплив початкових швидкостей, потрібно працювати при більших прискорюючих напругах.
. При цьому сила анодного струму Іа повинна різко зменшуватися (рис.2). Дослід показує, що при критичному значенні індукції магнітного поля анодний струм не падає стрибком до нуля, а плавно зменшується (рис.3). Такий хід залежності анодного струму частково пояснюється тим, що електрон, який вилетів з катода, вже має деяку швидкість. Величина її визначається тепловим рухом електронів всередині катода. Щоб зменшити вплив початкових швидкостей, потрібно працювати при більших прискорюючих напругах. Крім того, плавний спад кривої
Крім того, плавний спад кривої 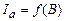 зумовлений некоаксіальністю катода і анода, наявністю залишкового газу в лампі, неоднорідністю поля соленоїда по висоті анода і т.д.
зумовлений некоаксіальністю катода і анода, наявністю залишкового газу в лампі, неоднорідністю поля соленоїда по висоті анода і т.д.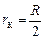 , одержимо
, одержимо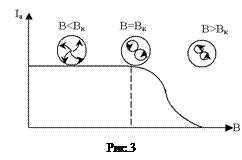
 . (8)
. (8) , (9)
, (9) ;
; 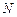 – число витків соленоїда.
– число витків соленоїда.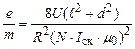 . (10)
. (10)
 відсутній різкий спад?
відсутній різкий спад?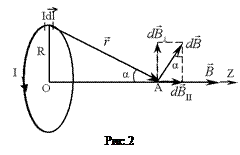
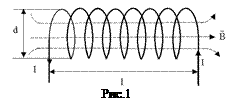 1. Соленоїд є системою послідовно з’єднаних однакових колових струмів (рис.1), тому для розрахунку індукції В магнітного поля в довільній точці на осі соленоїда потрібно спочатку розглянути магнітне поле на осі колового струму (одного витка соленоїда) (рис.2). Виберемо елемент струму
1. Соленоїд є системою послідовно з’єднаних однакових колових струмів (рис.1), тому для розрахунку індукції В магнітного поля в довільній точці на осі соленоїда потрібно спочатку розглянути магнітне поле на осі колового струму (одного витка соленоїда) (рис.2). Виберемо елемент струму  , визначається законом Біо-Савара-Лапласа (у вакуумі)
, визначається законом Біо-Савара-Лапласа (у вакуумі)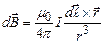 , (1)
, (1) – магнітна стала. При цьому
– магнітна стала. При цьому  можна розкласти на дві складові:
можна розкласти на дві складові:  – паралельну до осі Z і
– паралельну до осі Z і  – перпендикулярну до цієї осі. За принципом суперпозиції вектор індукції магнітного поля, створеного коловим струмом, тобто усіма елементами струму,
– перпендикулярну до цієї осі. За принципом суперпозиції вектор індукції магнітного поля, створеного коловим струмом, тобто усіма елементами струму,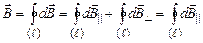 . (2)
. (2) і
і  , то після підстановки (1) у (2) отримаємо для індукції магнітного поля на осі колового струму
, то після підстановки (1) у (2) отримаємо для індукції магнітного поля на осі колового струму . (3)
. (3) )
) .
.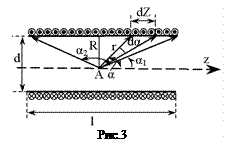 2. Для розрахунку індукції магнітного поля соленоїда розглянемо його осьовий переріз (рис.3),припускаючи постійність щільності намотки вздовж осі Z. Якщо на одиницю довжини соленоїда припадає n витків, то на ділянці довжиною dz буде ndz витків, які в точці А створять магнітне поле з індукцією
2. Для розрахунку індукції магнітного поля соленоїда розглянемо його осьовий переріз (рис.3),припускаючи постійність щільності намотки вздовж осі Z. Якщо на одиницю довжини соленоїда припадає n витків, то на ділянці довжиною dz буде ndz витків, які в точці А створять магнітне поле з індукцією . (4)
. (4) ,
,  , після інтегрування (4) по всій довжині соленоїда отримаємо для індукції магнітного поля на осі соленоїда
, після інтегрування (4) по всій довжині соленоїда отримаємо для індукції магнітного поля на осі соленоїда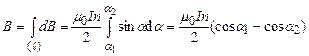 . (5)
. (5)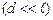 , то
, то  і
і  . Тоді
. Тоді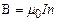 . (6)
. (6) слабка, поле найсильніше в центрі соленоїда і зменшується при наближенні до його кінців.
слабка, поле найсильніше в центрі соленоїда і зменшується при наближенні до його кінців. 3. Для визначення індукції магнітного поля на осі соленоїда в цій роботі використовуються напівпровідникові датчики, дія яких грунтується на ефекті Холла,–датчики Холла (ДХ) (рис.4). Нехай для ДХ використано напівпровідниковий кристал з дірковою провідністю (носії струму – дірки (hole)). Якщо вздовж такого кристалу протікає електричний струм з густиною
3. Для визначення індукції магнітного поля на осі соленоїда в цій роботі використовуються напівпровідникові датчики, дія яких грунтується на ефекті Холла,–датчики Холла (ДХ) (рис.4). Нехай для ДХ використано напівпровідниковий кристал з дірковою провідністю (носії струму – дірки (hole)). Якщо вздовж такого кристалу протікає електричний струм з густиною  і він розміщений в поперечному магнітному полі з індукцією
і він розміщений в поперечному магнітному полі з індукцією  , буде діяти сила Лоренца
, буде діяти сила Лоренца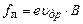 . (7)
. (7) , значення якої визначене з умови рівноваги
, значення якої визначене з умови рівноваги  становить
становить . (8)
. (8) . (9)
. (9) і концентрацією носіїв Р співвідношенням
і концентрацією носіїв Р співвідношенням 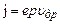 , то (9) перепишеться як
, то (9) перепишеться як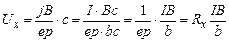 , (10)
, (10) – постійна Холла.
– постійна Холла. Оскільки значення
Оскільки значення  i
i  є фіксованими параметрами ДХ, а сила струму через кристал підтримується постійною (для ДХ цієї роботи
є фіксованими параметрами ДХ, а сила струму через кристал підтримується постійною (для ДХ цієї роботи  ), то доцільно ввести коефіцієнт пропорційності
), то доцільно ввести коефіцієнт пропорційності  , і тоді (10) запишеться як
, і тоді (10) запишеться як . (11)
. (11) . Ситуація дещо ускладнюється можливою нееквіпотенціальністю контактів 1, 2, що приво-дить до появи напруги нееквіпотенціальностї
. Ситуація дещо ускладнюється можливою нееквіпотенціальністю контактів 1, 2, що приво-дить до появи напруги нееквіпотенціальностї  навіть при відсутності магнітного поля. В цьому випадку
навіть при відсутності магнітного поля. В цьому випадку (12)
(12) – напруга, що вимірюється вольтметром з великим вхідним опором (чи потенціометром), приєднаним безпосередньо до контактів 1, 2 ДХ. Параметри
– напруга, що вимірюється вольтметром з великим вхідним опором (чи потенціометром), приєднаним безпосередньо до контактів 1, 2 ДХ. Параметри  а також кількість витків
а також кількість витків 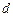 соленоїда задаються як паспортні дані блоку соленоїда.
соленоїда задаються як паспортні дані блоку соленоїда. який вимірюється амперметром А, а також струм ДХ (І=4mA). Датчик Холла розміщений на рухомому штоці з міліметровою шкалою, нульова позначка якої фіксує положення ДХ в центрі соленоїда. Напруга на зондових контактах датчика Холла вимірюється цифровим вольтметром з точністю до третього знаку після коми.
який вимірюється амперметром А, а також струм ДХ (І=4mA). Датчик Холла розміщений на рухомому штоці з міліметровою шкалою, нульова позначка якої фіксує положення ДХ в центрі соленоїда. Напруга на зондових контактах датчика Холла вимірюється цифровим вольтметром з точністю до третього знаку після коми. 1. Скласти схему, показану на рис.6 (при потребі).
1. Скласти схему, показану на рис.6 (при потребі). .
. , з кроком
, з кроком 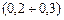 А. Дані занести в таблицю 1.
А. Дані занести в таблицю 1. , а за (11) –
, а за (11) –  при всіх значеннях струму
при всіх значеннях струму 


