
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Опис експериментальної установки та хід виконання роботиСодержание книги
Поиск на нашем сайте
1. Експериментальна установка складається з модуля ФПЕ–03, блока живлення (БЖ), міліамперметра. Принципова схема представлена на рис.4.
3. Встановити анодну напругу 4. Змінюючи силу струму в соленоїді при постійній анодній напрузі, зняти залежність анодного струму від струму соленоїда 5. Побудувати графік залежності 6. Обчислити відносну і абсолютну похибки вимірювання питомого заряду. Користуючись паспортними даними приладів, відносну похибку можна обчислити за формулою
Абсолютна похибка обчислюється за формулою.
7. Записати кінцевий результат.
Таблиця вимірювань U =, l =, d =, R =, N=, μ0=, Iск= Δ U 0=, Δ l 0=, Δd0=, ΔR0=, ΔN0=, Δ(μ0)0=, Δ(Iск)0=
Контрольні запитання 1. Яка будова магнетрона? Практичне використання магнетрона. 2. Описати електромагнітне поле в магнетроні. 3. Довести, що сила Лоренца не виконує роботи. 4. При яких умовах виникає сила Лоренца? Яка величина і напрям сили Лоренца? 5. Чому в залежності 6. Вивести робочу формулу. Лабораторна робота № 4.4 Вивчення магнітного поля соленоїда за допомогою датчика Холла Мета роботи: ознайомитися з холлівським методом вимірювання індукції магнітного поля; дослідити залежність індукції магнітного поля в центрі соленоїда від струму; дослідити осьову неоднорідність магнітного поля в соленоїді. Теоретичні відомості (теорію до даної роботи див. також у конспекті лекцій, §§4.2-4.3)
де
Тут враховано, що для усякого елементу
Зауважимо, що в центрі колового струму (
Врахувавши, що
Якщо соленоїд дуже довгий
Зауважимо, що формулу (6) можна отримати, використавши теорему про циркуляцію вектора індукції магнітного поля. Для дуже довгого соленоїда магнітне поле практично однорідне (силові лінії еквідистантні і паралельні до осі соленоїда). Для реальних соленоїдів, коли нерівність
Ця сила, як видно з рис.4, буде відхиляти носії до грані 1, і між гранями 1 та 2 виникне поперечне холлівське поле з напруженістю
Різниця потенціалів між гранями 1, 2 або холлівська напруга складає
Якщо врахувати, що густина струму пов’язана з
де І – сила струму через кристал, а
Отже, для визначення значення індукції магнітного поля соленоїда достатньо виміряти холлівську напругу між контактами 1–2 ДХ (рис.5) і помножити її на
де 4. Блок-схема експериментальної установки показана на рис.6. Блок живлення забезпечує регульований (регулятор Р) струм через соленоїд Хід роботи Завдання 1. Дослідження залежності магнітної індукції в центрі соленоїда від струму соленоїда.
2. Розмістити шток з ДХ в трубі соленоїда в положенні “0” по шкалі (центр соленоїда). 3. Ввімкнути в мережу ~220В БЖ і ЦВ, поставивши перемикач К в положення 4. Виміряти напругу 5. За формулою (12) розрахувати 6. Побудувати графік залежності Завдання 2. Дослідження осьової неоднорідності магнітного поля соленоїда. 1. Встановити задане викладачем значення 2. Переміщуючи шток з ДХ вздовж осі соленоїда з кроком 3. Побудувати графік залежності 4. Для центру соленоїда розрахувати В за формулами (5) та (6). Результати порівняти з експериментом; зробити висновки.
У звіт включити: мету роботи, блок-схему установки, формули (5), (6), (11), (12), табл.1, 2 з відповідними графіками, розрахунками та висновками.
Таблиці вимірювань
Контрольні запитання 1. Записати і пояснити закон Біо-Савара-Лапласа. 2. Вивести формулу для індукції магнітного поля на осі або в центрі колового струму. 3. Вивести формулу для індукції магнітного поля в центрі дуже довгого соленоїда, користуючись теоремою про циркуляцію вектора індукції магнітного поля. 4. Пояснити, в чому полягає ефект Холла. Лабораторна робота № 4.5 Визначення горизонтальної складової напруженості магнітного поля Землі Мета роботи: виміряти горизонтальну складову напруженості магнітного поля Землі. Теоретичні відомості
Тангенс-гальванометр – прилад для вимірювання горизонтальної складової напруженості магнітного поля Землі, складається з вертикально встановленої колової рамки, на яку намотано кілька витків ізольованого дроту. В центрі рамки знаходиться маленька магнітна стрілка, що може вільно обертатися в горизонтальній площині (рис.1)
де І – сила струму в рамці, N – кількість витків, R – радіус кола. Напрямок
Підставивши (1) в (2), одержимо
Хід роботи
2. Повертаючи рамку, встановити площину її витків паралельно до магнітної стрілки. 3. Скласти схему згідно рис.3. 4. Замкнути ключ К (перемикач П замкнений в довільному положенні) і за допомогою реостата підібрати таку силу струму, щоб кут відхилення стрілки 5. Дослід повторити ще два рази при незмінній силі струму, результати записати в таблицю і усереднити. 6. За формулою (3) знайти 7. Знайти абсолютні похибки прямих вимірювань величин 8. Знайти абсолютну та відносну похибки вимірювання
Увага! Величина 9. Записати кінцевий результат.
Таблиця вимірювань
Контрольні запитання 1. Сформулювати і записати закон Біо-Савара-Лапласа та принцип суперпозиції для магнітного поля. 2. Який зв’язок між магнітною індукцією та напруженістю магнітного поля? В яких одиницях вимірюються В та Н? 3. Вивести формулу для напруженості магнітного поля в центрі колового струму. 4. Пояснити будову і принцип дії тангенс-гальванометра. Вивести робочу формулу. 5. Чому магнітна стрілка тангенс-гальванометра повинна бути невеликого розміру? 6. Від чого залежить кут відхилення стрілки в даній роботі? 7. Чому похибка вимірювань найменша, коли кут відхилення Лабораторна робота №4.6 Визначення прискорення вільного падіння за допомогою оборотного маятника Мета роботи: вивчити основні фізичні властивості оборотного маятника і визначити за його допомогою прискорення вільного падіння. Теоретичні відомості (теорію до даної роботи див. також у конспекті лекцій, §§5.1-5.3)
де g – прискорення вільного падіння, L – зведена довжина фізичного маятника,
I – момент інерції маятника відносно осі обертання, що проходить через точку О, m – маса маятника, l – віддаль від осі обертання до центра мас. Точка К, що лежить на лінії ОС і віддалена від точки О на зведену довжину L маятника, називається центром коливань. Якщо такий маятник буде здійснювати коливання відносно осі, що проходить через точку К, то період коливань буде рівний періоду коливань відносно осі, що проходить через точку O. Тому точки К і О називають спряженими. Маятник, котрий може коливатися відносно двох спряжених точок, називається оборотним. Покажемо, що періоди коливань відносно осей, що проходять через точки К і О, однакові. Позначимо зведену довжину фізичного маятника при коливаннях відносно осі, що проходить через точку К, через Зведені довжини при коливаннях маятника відносно осей, що проходять через точки К і О,
де
( З (2) і (3) одержимо
З рис. 1 видно, що
Враховуючи перше з рівнянь (4), з (6) одержимо Практично підібрати такі точки О і К, відносно яких періоди коливань маятника були б однакові, важко. Оскільки періоди коливань дещо відрізняються, то згідно з формулами (1), (3) та (4) маємо
Виключаючи з рівнянь (7)
Якщо маятник оборотний, тобто
Остання формула використовується для визначення прискорення вільного падіння.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.53.112 (0.013 с.) |

 2. Скласти схему, показану на рис.4.
2. Скласти схему, показану на рис.4. по вольтметру блока живлення.
по вольтметру блока живлення. . Дані занести в таблицю.
. Дані занести в таблицю.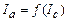 і визначити на ньому критичний струм
і визначити на ньому критичний струм  . Значення
. Значення  вибирається на кривій
вибирається на кривій 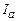 починає спадати.
починає спадати.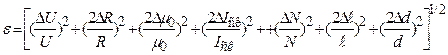 .
.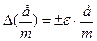 .
.
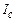
 відсутній різкий спад?
відсутній різкий спад?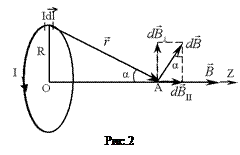
 1. Соленоїд є системою послідовно з’єднаних однакових колових струмів (рис.1), тому для розрахунку індукції В магнітного поля в довільній точці на осі соленоїда потрібно спочатку розглянути магнітне поле на осі колового струму (одного витка соленоїда) (рис.2). Виберемо елемент струму
1. Соленоїд є системою послідовно з’єднаних однакових колових струмів (рис.1), тому для розрахунку індукції В магнітного поля в довільній точці на осі соленоїда потрібно спочатку розглянути магнітне поле на осі колового струму (одного витка соленоїда) (рис.2). Виберемо елемент струму  . Вектор індукції магнітного поля, породженого цим елементом в точці А, положення котрої задається радіус-вектором
. Вектор індукції магнітного поля, породженого цим елементом в точці А, положення котрої задається радіус-вектором  , визначається законом Біо-Савара-Лапласа (у вакуумі)
, визначається законом Біо-Савара-Лапласа (у вакуумі)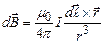 , (1)
, (1) – магнітна стала. При цьому
– магнітна стала. При цьому  можна розкласти на дві складові:
можна розкласти на дві складові:  – паралельну до осі Z і
– паралельну до осі Z і  – перпендикулярну до цієї осі. За принципом суперпозиції вектор індукції магнітного поля, створеного коловим струмом, тобто усіма елементами струму,
– перпендикулярну до цієї осі. За принципом суперпозиції вектор індукції магнітного поля, створеного коловим струмом, тобто усіма елементами струму,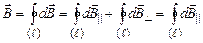 . (2)
. (2) і
і  , то після підстановки (1) у (2) отримаємо для індукції магнітного поля на осі колового струму
, то після підстановки (1) у (2) отримаємо для індукції магнітного поля на осі колового струму . (3)
. (3) )
) .
.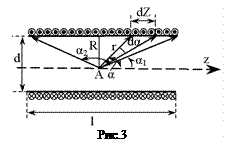 2. Для розрахунку індукції магнітного поля соленоїда розглянемо його осьовий переріз (рис.3),припускаючи постійність щільності намотки вздовж осі Z. Якщо на одиницю довжини соленоїда припадає n витків, то на ділянці довжиною dz буде ndz витків, які в точці А створять магнітне поле з індукцією
2. Для розрахунку індукції магнітного поля соленоїда розглянемо його осьовий переріз (рис.3),припускаючи постійність щільності намотки вздовж осі Z. Якщо на одиницю довжини соленоїда припадає n витків, то на ділянці довжиною dz буде ndz витків, які в точці А створять магнітне поле з індукцією . (4)
. (4) ,
,  , після інтегрування (4) по всій довжині соленоїда отримаємо для індукції магнітного поля на осі соленоїда
, після інтегрування (4) по всій довжині соленоїда отримаємо для індукції магнітного поля на осі соленоїда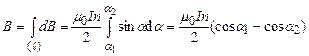 . (5)
. (5)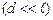 , то
, то  і
і  . Тоді
. Тоді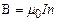 . (6)
. (6) слабка, поле найсильніше в центрі соленоїда і зменшується при наближенні до його кінців.
слабка, поле найсильніше в центрі соленоїда і зменшується при наближенні до його кінців. 3. Для визначення індукції магнітного поля на осі соленоїда в цій роботі використовуються напівпровідникові датчики, дія яких грунтується на ефекті Холла,–датчики Холла (ДХ) (рис.4). Нехай для ДХ використано напівпровідниковий кристал з дірковою провідністю (носії струму – дірки (hole)). Якщо вздовж такого кристалу протікає електричний струм з густиною
3. Для визначення індукції магнітного поля на осі соленоїда в цій роботі використовуються напівпровідникові датчики, дія яких грунтується на ефекті Холла,–датчики Холла (ДХ) (рис.4). Нехай для ДХ використано напівпровідниковий кристал з дірковою провідністю (носії струму – дірки (hole)). Якщо вздовж такого кристалу протікає електричний струм з густиною  і він розміщений в поперечному магнітному полі з індукцією
і він розміщений в поперечному магнітному полі з індукцією  , то на носії струму, заряд яких е, і які рухаються з дрейфовою швидкістю
, то на носії струму, заряд яких е, і які рухаються з дрейфовою швидкістю  , буде діяти сила Лоренца
, буде діяти сила Лоренца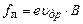 . (7)
. (7) , значення якої визначене з умови рівноваги
, значення якої визначене з умови рівноваги  становить
становить . (8)
. (8) . (9)
. (9) і концентрацією носіїв Р співвідношенням
і концентрацією носіїв Р співвідношенням 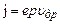 , то (9) перепишеться як
, то (9) перепишеться як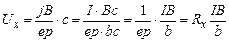 , (10)
, (10) – постійна Холла.
– постійна Холла. Оскільки значення
Оскільки значення  i
i  є фіксованими параметрами ДХ, а сила струму через кристал підтримується постійною (для ДХ цієї роботи
є фіксованими параметрами ДХ, а сила струму через кристал підтримується постійною (для ДХ цієї роботи  ), то доцільно ввести коефіцієнт пропорційності
), то доцільно ввести коефіцієнт пропорційності  , і тоді (10) запишеться як
, і тоді (10) запишеться як . (11)
. (11) . Ситуація дещо ускладнюється можливою нееквіпотенціальністю контактів 1, 2, що приво-дить до появи напруги нееквіпотенціальностї
. Ситуація дещо ускладнюється можливою нееквіпотенціальністю контактів 1, 2, що приво-дить до появи напруги нееквіпотенціальностї  навіть при відсутності магнітного поля. В цьому випадку
навіть при відсутності магнітного поля. В цьому випадку (12)
(12) – напруга, що вимірюється вольтметром з великим вхідним опором (чи потенціометром), приєднаним безпосередньо до контактів 1, 2 ДХ. Параметри
– напруга, що вимірюється вольтметром з великим вхідним опором (чи потенціометром), приєднаним безпосередньо до контактів 1, 2 ДХ. Параметри  а також кількість витків
а також кількість витків 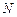 , довжина
, довжина  і діаметр
і діаметр 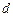 соленоїда задаються як паспортні дані блоку соленоїда.
соленоїда задаються як паспортні дані блоку соленоїда. який вимірюється амперметром А, а також струм ДХ (І=4mA). Датчик Холла розміщений на рухомому штоці з міліметровою шкалою, нульова позначка якої фіксує положення ДХ в центрі соленоїда. Напруга на зондових контактах датчика Холла вимірюється цифровим вольтметром з точністю до третього знаку після коми.
який вимірюється амперметром А, а також струм ДХ (І=4mA). Датчик Холла розміщений на рухомому штоці з міліметровою шкалою, нульова позначка якої фіксує положення ДХ в центрі соленоїда. Напруга на зондових контактах датчика Холла вимірюється цифровим вольтметром з точністю до третього знаку після коми. 1. Скласти схему, показану на рис.6 (при потребі).
1. Скласти схему, показану на рис.6 (при потребі). .
. , з кроком
, з кроком 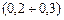 А. Дані занести в таблицю 1.
А. Дані занести в таблицю 1. , а за (11) –
, а за (11) –  при всіх значеннях струму
при всіх значеннях струму  . Зробити висновок.
. Зробити висновок.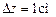 , виміряти
, виміряти  . Зробити висновок.
. Зробити висновок.
 Таблиця 1
Таблиця 1 ,
А
,
А



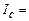
 Таблиця 2
Таблиця 2
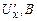


 (теорію до даної роботи див. також у конспекті лекцій, §§ 4.1, 4.2)
(теорію до даної роботи див. також у конспекті лекцій, §§ 4.1, 4.2) Якщо по рамці проходить електричний струм, то напруженість створеного ним магнітного поля можна розрахувати за законом Біо-Савара-Лапласа. В центрі кола вона визначається за формулою
Якщо по рамці проходить електричний струм, то напруженість створеного ним магнітного поля можна розрахувати за законом Біо-Савара-Лапласа. В центрі кола вона визначається за формулою 
 , (1)
, (1)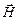 визначається за правилом свердлика і співпадає з нормаллю до площини рамки. Крім того, навколо Землі існує магнітне поле, напрямок напруженості якого співпадає з напрямком магнітного меридіана. При проходженні струму через котушку напруженість результуючого магнітного поля, згідно з принципом суперпозиції, дорівнює векторній сумі напруженостей поля Землі і поля колового струму. Якщо площина колового струму збігається з площиною магнітного меридіана, то горизонтальна складова напруженості магнітного поля Землі
визначається за правилом свердлика і співпадає з нормаллю до площини рамки. Крім того, навколо Землі існує магнітне поле, напрямок напруженості якого співпадає з напрямком магнітного меридіана. При проходженні струму через котушку напруженість результуючого магнітного поля, згідно з принципом суперпозиції, дорівнює векторній сумі напруженостей поля Землі і поля колового струму. Якщо площина колового струму збігається з площиною магнітного меридіана, то горизонтальна складова напруженості магнітного поля Землі  лежить у площині колового струму, а напруженість
лежить у площині колового струму, а напруженість  може бути знайдена геометрично за правилом паралелограма (рис.2). Магнітна стрілка, котра у відсутності струму орієнтувалася вздовж
може бути знайдена геометрично за правилом паралелограма (рис.2). Магнітна стрілка, котра у відсутності струму орієнтувалася вздовж 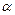 і встановлюється вздовж напрямку результуючого поля
і встановлюється вздовж напрямку результуючого поля  . Як видно з рис.2
. Як видно з рис.2 . (2)
. (2) . (3)
. (3) 1. Повертаючи тангенс-гальванометр у горизонтальній площині, встановити його так, щоб кінець магнітної стрілки збігався з нулем шкали.
1. Повертаючи тангенс-гальванометр у горизонтальній площині, встановити його так, щоб кінець магнітної стрілки збігався з нулем шкали. і
і  по обох її кінцях. Змінивши перемикачем П напрямок струму на протилежний, виміряти кути відхилення стрілки
по обох її кінцях. Змінивши перемикачем П напрямок струму на протилежний, виміряти кути відхилення стрілки  і
і 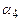 .
. .
.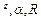 .
.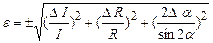 . (4)
. (4) . (5)
. (5) в (5) має бути виражена в радіанах.
в (5) має бути виражена в радіанах.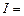



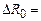


 Оборотний маятник – частковий випадок фізичного маятника. Фізичним маятником називається будь-яке тверде тіло, котре може коливатися у полі тяжіння навколо горизонтальної осі, що не проходить через його центр мас. Точка перетину О осі з вертикальною площиною, що проходить через центр мас С маятника називається точкою підвісу. При рівноважному положенні маятника точки О і С знаходяться на одній вертикалі, причому центр мас розміщений нижче точки підвісу (рис. 1). Якщо відхилити маятник на невеликий кут і відпустити його, то він буде здійснювати гармонічні коливання з періодом
Оборотний маятник – частковий випадок фізичного маятника. Фізичним маятником називається будь-яке тверде тіло, котре може коливатися у полі тяжіння навколо горизонтальної осі, що не проходить через його центр мас. Точка перетину О осі з вертикальною площиною, що проходить через центр мас С маятника називається точкою підвісу. При рівноважному положенні маятника точки О і С знаходяться на одній вертикалі, причому центр мас розміщений нижче точки підвісу (рис. 1). Якщо відхилити маятник на невеликий кут і відпустити його, то він буде здійснювати гармонічні коливання з періодом , (1)
, (1)
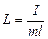 . (2)
. (2) . Якщо доведемо, що
. Якщо доведемо, що  , то цим згідно з формулою (1) буде доведено, що періоди коливань відносно осей, котрі проходять через точки К і О, однакові.
, то цим згідно з формулою (1) буде доведено, що періоди коливань відносно осей, котрі проходять через точки К і О, однакові. , (3)
, (3) і
і  – моменти інерції маятника відносно відповідних осей. За теоремою Штейнера
– моменти інерції маятника відносно відповідних осей. За теоремою Штейнера (4)
(4)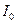 – момент інерції маятника відносно осі, що проходить через центр мас).
– момент інерції маятника відносно осі, що проходить через центр мас).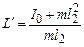 . (5)
. (5) . Підставляючи це співвідношення у (5), одержимо
. Підставляючи це співвідношення у (5), одержимо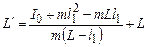 . (6)
. (6) , що і потрібно було довести.
, що і потрібно було довести. . (7)
. (7) , знайдемо
, знайдемо . (8)
. (8)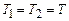 , то з (3) одержимо
, то з (3) одержимо . (9)
. (9)


