
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Гаусса за допомогою ExcelСодержание книги
Поиск на нашем сайте
Задача 1. Розв’язати СЛР Розв’язання. Запишемо розширену матрицю даної СЛР у діапазон А2:С4
Тут і надалі доцільно підкреслити всі границі цієї таблиці, натиснувши кнопку Границы → Все границы на панелі Форматирование: це дасть змогу не рахувати потім номер рядка чи стовпця при подальших обчисленнях. На першому кроці алгоритму наша мета – досягти того, щоби в результаті послідовності елементарних операцій над матрицею під рядком 2 у стовпці А значення чарунок дорівнювали нулю. Це і реалізує така електронна таблиця:
Тут формули для матричних операцій над рядком (ті ж самі, що й у попередньому прикладі) записуються в одну чарунку, а потім розповсюджуються на весь рядок, просто перетягнувши маркер заповнення згідно з правилами Excel. Ф ормули треба виконувати спочатку у першому стовпці (тобто у стовпці 6), а потім у стовпцях 7 і 8. В результаті дістанемо:
На другому кроці треба отримати 1 для елемента матриці, відповідного В7 і 0 для елементів, відповідних В6 і В8. Це реалізує така електронна таблиця:
Тут формули для матричних операцій записуються у чарунки стовпця В, а потім копіюються на відповідні рядки. Ф ормули треба виконувати спочатку у другому стовпці (тобто у стовпці 11), а потім у стовпцях 10 і 12. В результаті дістанемо:
Нарешті, на третьому кроці треба отримати 1 для елемента матриці, відповідного С12 і 0 для елементів, відповідних С10 і С11.
Ф ормули треба виконувати спочатку у стовпці 12, а потім у 10 і 11. В результаті:
Матриця приведена до діагональної форми. Отже, розв’язок даної СЛР:
Похибка методу Гаусса дорівнює нулю (і в такому сенсі це точний метод), обчислювальна похибка отриманого розв’язку не перевищує мінімальної можливої похибки Excel, помноженої на кількість зроблених операцій, тобто насправді майже не відрізняється від цієї мінімальної похибки. Проте переконаємося у правильності отриманого розв’язку безпосередньо, підставивши його у всі рівняння даної СЛР згідно з означенням розв’язку. Для цього зручно буде мати цей розв’язок у горизонтальному діапазоні. Тому скопіюємо чарунки D14:D15, виділимо чарунку А18, клацнімо по ній правою кнопкою миші і в контекстному меню обираємо Специальная вставка і у наступному діалозі клацніть по значения і транспонировать (знизу вікна). Розв’язок з’явиться у діапазоні А18:С18. У чарунці D18 задамо формулу = СУММПРОИЗВ($A$18:$C$18; A2:C2), яка підраховує результат підстановки розв’язку у перше рівняння системи. Після цього перетягнемо маркер заповнення з D18 на дві чарунки вниз – там з’являться підрахунки результатів підстановки у друге та третє рівняння розв’язку згідно з правилами копіювання формул в Excel:
Значення в діапазоні D18:D20 точно співпадають з вільними членами даної СЛР у D2:D4, що є безпосереднім доведенням правильності отриманого розв’язку.
2х1 – 3х2 + х3 – 2х4 = – 2 4х1 – х2 + 2х3 – х4 = 0. Розв’язання. Запишемо розширену матрицю даної СЛР у діапазон А2:Е4
– це система трьох лінійних рівнянь з чотирма змінними. Проте метод Гаусса – алгоритм, який дозволяє розв’язати будь – яку СЛР. Послідовність дій фактично не відрізняється від попереднього прикладу. Перший крок:
В результаті:
Другий крок:
Тут елементи матриці – цілі числа, тому зручно у формулах замість адреси чарунки використати саме значення. В результаті:
Третій крок:
звідки
Матриця у діапазоні А14:С16 зведена до діагонального вигляду, що завершує алгоритм. Отриманій матриці відповідає така СЛР:
У чарунку F17 замість * можна занести довільне значення змінної х4 і в діапазоні F14:F17 дістанемо відповідний частковий розв’язок даної СЛР. Наприклад,
або
Перевірку правильності отриманих розв’язків можна провести, як і раніше. А саме скопіюємо чарунки F14:F17 у горизонтальний діапазон А19:D19, задамо формулу = СУММПРОИЗВ($A$19:$D$19;A2:D2), яка підраховує значення результату підстановки розв’язку у перше рівняння і перетягнемо маркер заповнення на дві чарунки вниз – там з’являться підрахунки результатів підстановки у друге та третє рівняння розв’язку згідно з правилами копіювання формул в Excel:
Задача 3. Розв’язати СЛР 3х1 – 2х2 + х3 = 2 2х1 – 3х2 + 2х3 = –1 х1 – х2 + 3х3 = 0 2х1 – 4х2 + 2х3 = 3. Розв’язання. Запишемо розширену матрицю даної СЛР у діапазон А2:D5
– це система чотирьох лінійних рівнянь з трьома змінними. Але метод Гаусса – алгоритм, послідовність дій така ж, як у попередньому прикладі. Перший крок:
В результаті:
Оскільки елементи початкової матриці цілі числа, то обрано дрібний формат чарунок. Другий крок:
звідки
Третій крок:
звідки
Матриця у діапазоні А17:С19 зведена до діагонального вигляду, що завершує алгоритм. Отриманій матриці відповідає така СЛР: Три наведених приклада у деякому сенсі вичерпують всі випадки, які можуть зустрітися при розв’язанні будь – якої системи m лінійних рівнянь з n змінними. Справді, нехай дана система m лінійних рівнянь з n змінними уже зведена до діагональної форми максимально можливого розміру p. Тоді р £ m, p £ n. В такій формі всі елементи m – p рядків матриці системи під діагональною матрицею дорівнюють нулю (рисунок 1). Справді, елементи
1 * 1 0 * p 1 р * 0 … * * ………………. * * * * * * * m 0 0 0 0 … 1 * 0 0 0 0 … 0 0 0 0 0 0 0 *
……………………………………. *
0 0 0 0 … 0 0 0 0 0 0 0 *
Рисунок 1.
під діагональною матрицею у перших р стовпцях дорівнюють нулю за алгоритмом. Якщо б серед інших елементів цих рядків залишився елемент, відмінний від нуля, то алгоритм мав би продовження і в результаті отримали б діагональну матрицю порядку > p. Отже, 1) якщо є принаймні один елемент стовпця n + 1 (стовпця вільних членів) bj ¹ 0 з j > p, то такому стовпцю j відповідає рівняння 0 = bj. Звідси отримана СЛР не має розв’язків (несумісна), а тому несумісна й рівносильна їй початкова СЛР (як у задачі 3). Якщо ж при j > p всі bj = 0, то всі рядки розширеної матриці системи під діагональною можна просто відкинути, не порушуючи еквівалентності, оскільки відповідні рівняння перетворюються у тотожності 0 = 0. В результаті отримуємо p ´ n матрицю (рисунок 2):
1 * 1 0 * * p 1 р * 0 … * ………………. * * * * * * * 0 0 0 0 … 1 *
Рисунок 2.
2) Якщо деякий стовпець такої матриці системи з і > p складаються лише з елементів, рівних нулю, то такий стовпець (і відповідну йому змінну хі) можна просто відкинути, не порушуючи еквівалентності. Отже, можна вважати, що всі стовпці матриці такої системи мають елементи, відмінні від нуля. В такому разі, якщо n > p, то відповідна СЛР сумісна і невизначена (як у задачі 2): всі змінні хі з і > p є вільними і кожному набору вільних змінних відповідає розв’язок даної СЛР. 3) Якщо n = p, то матриця системи є квадратною та діагональною і отже елементи bj стовпця р + 1 (стовпця вільних членів) утворюють єдиний розв’язок даної СЛР: система сумісна та визначена (як у задачі 1). Зауваження. З попереднього ясно: якщо число рівнянь m перевищує число змінних n, то, як правило, така СЛР несумісна (як у задачі 3). Якщо m < n, то, як правило, така СЛР сумісна і невизначена (як у задачі 2). Якщо m = n, то така СЛР, як правило, сумісна та визначена (як у задачі 1). Тут сказано «як правило», бо спеціальний підбір коефіцієнтів може це правило порушити. Розглянемо такий приклад.
2х2 – х3 = – 3 х1 + 3х2 – 2х3 = 2 2х1 +10х2 – 6х3 = – 2.
Розв’язання. Зведемо розширену матрицю даної СЛР до діагональної форми так само, як і в попередніх прикладах. В результаті отримуємо:
Тут ми 1) переставляємо місцями перший і другий рядки, 2) віднімаємо з третього рядка перший, помножений на 2, 3) ділимо другий рядок на 2 і віднімаємо від першого отриманий рядок, помножений на 3, і від третього цей рядок, помножений на 4. Останній рядок складається з нулів, тому відкидаємо його і отримуємо загальний розв’язок:
х2 = - 1,5 + 0,5х3. Отже, дана система трьох лінійних рівнянь з трьома змінними сумісна та невизначена.
Матричні операції в Excel
Звичайно, матриці використовуються не лише для компактного запису розв’язування СЛР методом Гаусса. Насправді це один з найбільш важливих математичних об’єктів. Над матрицями визначені операції подібні операціям над числами. 1. Множення матриці на число:
а11…..а1n α×а11 ... α×а1n α ∙ ………... = ……….. аm1 … аm n α×аm1 … α×аm n,
де α – дійсне число. Наприклад, для множення матриці
В результаті дістанемо
2. Додавання та віднімання m
………... аm1 … аm n bm1… bm n аm1
Наприклад, для підрахунку матриці, що дорівнює
В результаті дістанемо
Для матриць, у яких не співпадають число рядків або число стовпців операції додавання та віднімання не визначені. Так не існує матриці, що дорівнює
4 0 -2 + 0 -1.
Задача 1. Знайти матрицю X =
Розв’язання. Матриця Х існує, оскільки всі матриці у її визначенні мають один розмір. Для підрахунків використаємо таблицю
У чарунці А11 замість наведеної у таблиці можна задати також формулу =$А$1*А2+$А$4*А5+$А$7*А8. В обох випадках дістанемо Х в діапазоні А11:С12:
3. Множення матриць. Добуток m Для множення матриць є спеціальний вбудований оператор Excel МУМНОЖ. Наприклад, у наступній електронній таблиці
задані 3 ´ 2 матриця А =
Після цього, притримуючи кнопки Alt i Shift, треба натиснути не Enter. В результаті отримаємо матрицю С:
Якщо спробувати помножити матриці А і В з нерівними числами стовпців у А та рядків у В, то отримаємо повідомлення про помилку #ЗНАЧ!. 4. Матриця, обернена до квадратної матриці А порядку n – це така квадратна матриця А-1 того ж порядку, що А А-1 = А-1 А = Е, де Е – одинична матриця. Якщо А має обернену, то її можна знайти методом Гаусса. Розглянемо n ´ 2n матрицю АЕ, яку можна отримати, дописавши праворуч від матриці А одиничну матрицю того ж порядку. Наприклад, якщо А = Справді, як ми бачили вище, якщо звести до діагональної форми СЛР з матрицею системи А, то стовпець вільних членів у розширеній матриці цієї системи є розв’язком даної СЛР. Тому перший стовпець матриці В є розв’язком СЛР Ах = Задача 2. Знайти матрицю, обернену до матриці А = Розв’язання. Задамо в електронній таблиці матрицю АЕ:
Зведемо її до діагональної так само, як і в попередньому параграфі:
Отже, матриця В = –0,06376 0,263775 0,055257 є оберненою до матриці А. Це 0,044086 0,091324 0,298241 можна перевірити безпосередньо за означенням за допомогою вбудованого оператора МУМНОЖ. Результат множення А на В, тобто результат дії оператору МУМНОЖ(A1:C3; D13:F15) дорівнює
Оскільки числа ~ 10-17 з точки зору Excel не відрізняються від нуля, то отримана матриця є одиничною. Якщо є сумнів, то можна змінити формат чарунки з общий на числовой. Тоді дістанемо
Знайти обернену матрицю можна також і за допомогою спеціального вбудованого оператора Excel МОБР. Треба виділити квадратний діапазон того ж розміру, що й у даної матриці, (в цьому прикладі з 9 чарунок), задати в ньому цей оператор, єдиним аргументом якого є діапазон даної матриці (тут це МОБР(А1:С3)) і притримуючи кнопки Alt i Shift, натиснути не Enter. Результат в даному випадку просто співпадає з отриманим вище методом Гаусса. Звичайно, не кожна квадратна матриця А має звернену, тільки та, визначник якої не дорівнює нулю: ôАô ¹ 0. Тому перед безпосереднім розв’язуванням задачі 2 було б доцільно знайти визначник даної матриці. Це можна зробити за допомогою відповідного вбудованого оператора Excel МОПРЕД. Треба виділити чарунку і задати там цей оператор, єдиним аргументом якого є діапазон заданої матриці. Після цього можна натиснути ОК або Enter: на відміну від МОБР та МУМНОЖ результатом дії цього оператора є числове значення, а не масив чарунок. В даному прикладі формула МОПРЕД(А1:С3) дає значення визначника ôАô = 55,01051. Якщо значення визначника матриці відмінне від нуля, але досить мале порівняно з її елементами, то відповідна СЛР погано обумовлена. СЛР називають добре обумовленою, якщо малі збурення коефіцієнтів мало збурюють її розв’язки і в противному разі погано обумовленою. Наприклад, СЛР
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 463; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.107.148 (0.015 с.) |

 .
. .
. Задача 2. Розв’язати СЛР х1 – 2х2 + 3х3 – 2х4 = 3
Задача 2. Розв’язати СЛР х1 – 2х2 + 3х3 – 2х4 = 3 . Тут за означенням змінні х1, х2, х3, яким відповідають діагональні елементи матриці – це основні (базові) змінні, всі інші (тут тільки х4) – неосновні (вільні). Переносимо у рівняннях СЛР вільні змінні зліва направо:
. Тут за означенням змінні х1, х2, х3, яким відповідають діагональні елементи матриці – це основні (базові) змінні, всі інші (тут тільки х4) – неосновні (вільні). Переносимо у рівняннях СЛР вільні змінні зліва направо:  і отримаємо загальний розв’язок: кожному значенню вільної змінної відповідає свій (частковий) розв’язок і всі розв’язки СЛР мають такий вигляд. В електронній таблиці їх можна отримувати так:
і отримаємо загальний розв’язок: кожному значенню вільної змінної відповідає свій (частковий) розв’язок і всі розв’язки СЛР мають такий вигляд. В електронній таблиці їх можна отримувати так: У чарунці Е14 тут знаходиться значення, яке з точки зору Excel не відрізняється від нуля. Отже, відповідь:
У чарунці Е14 тут знаходиться значення, яке з точки зору Excel не відрізняється від нуля. Отже, відповідь:  або
або  – це приклади часткових розв’язків.
– це приклади часткових розв’язків. . Останнє рівняння виписано із всіма нульовими коефіцієнтами. Яким би не був набір значень х1, х2 , х3, в результаті їх підстановки в останнє рівняння отримаємо протиріччя: 0 = 5 1/3. Отже, це рівняння, а тому і вся система не мають розв’язків. Але звідси несумісною є й початкова СЛР, еквівалентна кінцевій. Відповідь: розв’язків не існує.
. Останнє рівняння виписано із всіма нульовими коефіцієнтами. Яким би не був набір значень х1, х2 , х3, в результаті їх підстановки в останнє рівняння отримаємо протиріччя: 0 = 5 1/3. Отже, це рівняння, а тому і вся система не мають розв’язків. Але звідси несумісною є й початкова СЛР, еквівалентна кінцевій. Відповідь: розв’язків не існує. n
n p
p





 p
p

 Задача 4. Розв’язати наступну СЛР методом Гаусса.
Задача 4. Розв’язати наступну СЛР методом Гаусса. х1 = 6,5 + 0,5х3
х1 = 6,5 + 0,5х3



 на число – 3 складемо таку таблицю
на число – 3 складемо таку таблицю n – матриць (тобто матриць з m строками та n стовпцями).
n – матриць (тобто матриць з m строками та n стовпцями).




 а11…..а1n b11... b1n а11
а11…..а1n b11... b1n а11  b11
b11  а1n
а1n  аm n
аm n  складемо таку таблицю
складемо таку таблицю

 .
. на 2 ´ 2 матрицю В =
на 2 ´ 2 матрицю В =  С = А×В не існує, оскільки число стовпців матриці А дорівнює 3 і не дорівнює числу рядків матриці В.
С = А×В не існує, оскільки число стовпців матриці А дорівнює 3 і не дорівнює числу рядків матриці В.
 і 2 ´ 3 матриця В =
і 2 ´ 3 матриця В = 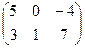 . Для знаходження 3 ´ 3 матриці С = А×В виділимо діапазон А5:С7 і (можливо за допомогою вікна цього оператора) введемо в нього формулу =МУМНОЖ(А1:В3;D1:F2).
. Для знаходження 3 ´ 3 матриці С = А×В виділимо діапазон А5:С7 і (можливо за допомогою вікна цього оператора) введемо в нього формулу =МУМНОЖ(А1:В3;D1:F2). , то АЕ =
, то АЕ =  . Зведемо матрицю АЕ до діагональної форми методом Гаусса. Тоді вона отримає вигляд ЕВ, де В – деяка квадратна матриця порядку n. Наприклад при n = 3 ЕВ =
. Зведемо матрицю АЕ до діагональної форми методом Гаусса. Тоді вона отримає вигляд ЕВ, де В – деяка квадратна матриця порядку n. Наприклад при n = 3 ЕВ =  . Стверджується, що така матриця В і є обернена до А, тобто В = А-1.
. Стверджується, що така матриця В і є обернена до А, тобто В = А-1. , наприклад,
, наприклад,  =
=  , тобто
, тобто  =
=  , наприклад,
, наприклад,  =
=  , тобто
, тобто  =
=  методом Гаусса.
методом Гаусса.
 0,236737 0,069816 0,042881
0,236737 0,069816 0,042881 , розв’язком якої є пара (1; 0) погано обумовлена. Справді, якщо число 6,1 у правій частині першого рівняння змінити на 0,02, то СЛР
, розв’язком якої є пара (1; 0) погано обумовлена. Справді, якщо число 6,1 у правій частині першого рівняння змінити на 0,02, то СЛР  матиме розв’язком пару (5,1; - 7,35). Якщо коефіцієнт 6,1 у лівій частині першого рівняння змінити на 0,01, то розв’язком СЛР
матиме розв’язком пару (5,1; - 7,35). Якщо коефіцієнт 6,1 у лівій частині першого рівняння змінити на 0,01, то розв’язком СЛР  буде пара (0,36730972; 1,204918). Причиною поганої обумовленості цієї системи є її майже виродженість: її визначник дорівнює 0,04 і становить лише 0,27% значення найбільшого з коефіцієнтів системи 14,7.
буде пара (0,36730972; 1,204918). Причиною поганої обумовленості цієї системи є її майже виродженість: її визначник дорівнює 0,04 і становить лише 0,27% значення найбільшого з коефіцієнтів системи 14,7.


