

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Кратний перерахунок для методів Рунге – Кутта за допомогою Excel
Задача 2. Знайти чисельні розв’язки задачі Коші  на відрізку [1; 2] з кроками інтегрування h = 0,1 0,05 методом Рунге – Кутта другого порядку точності по формулам на відрізку [1; 2] з кроками інтегрування h = 0,1 0,05 методом Рунге – Кутта другого порядку точності по формулам  , де , де  , і оцінити похибку отриманого розв’язку методом подвійного перерахунку. , і оцінити похибку отриманого розв’язку методом подвійного перерахунку.
Розв’язання. Оскільки за формулою q = 2, то в такому разі метод Рунге – Кутта має другий порядок точності тоді і тільки тоді, коли його параметри задовольняють (5). Тут  , тож α2 = , тож α2 =  , звідки β21 = , звідки β21 =  , р2 = 1, р1 = 0. Отже, , р2 = 1, р1 = 0. Отже,  , де , де  , ,  = yk + = yk +  h f (xk, yk). Це удосконалений метод Ейлера. Кроки інтегрування задамо у чарунках H1, H2: тут H1 = 0,1, H2 = 0,05. Побудуємо електронну таблицю для чисельного розв’язання даної задачі Коші з кроком інтегрування 0,1 по таким формулам. Надамо чарункам таких значень: h f (xk, yk). Це удосконалений метод Ейлера. Кроки інтегрування задамо у чарунках H1, H2: тут H1 = 0,1, H2 = 0,05. Побудуємо електронну таблицю для чисельного розв’язання даної задачі Коші з кроком інтегрування 0,1 по таким формулам. Надамо чарункам таких значень:
|
| A
| B
| C
| |
| x
| y
| w1
| |
|
|
| = $H$1*(2*A2+3*SIN(B2^2))
| |
| = A2 + $H$1
| = B2 + F2
| ↓
| |
| ↓
| ↓
| ↓
| |
| D
| E
| F
| |
| x1
| y1
| w2
| |
| = A2 + 0,5*$H$1
| = B2 + 0,5*C2
| =$H$1*(2*D2+3*SIN(E2^2))
| |
| ↓
| ↓
| ↓
|
Тут у стовпці С значення w1(h) = h f (xk, yk), у стовпці F значення w2(h) = h f ( , ,  ). Нагадаємо, що формулу у чарунці F2 можна просто скопіювати з чарунки С2. В результаті обрахунків за попередньою таблицею дістанемо: ). Нагадаємо, що формулу у чарунці F2 можна просто скопіювати з чарунки С2. В результаті обрахунків за попередньою таблицею дістанемо:
|
| A
| B
| C
| D
| E
| F
| |
| х
| у
| w1
| х1
| у1
| w2
| |
|
|
| 0,2
| 1,05
| 0,1
| 0,213
| |
| 1,1
| 0,213
| 0,233606
| 1,15
| 0,329803
| 0,262567
| |
| 1,2
| 0,475567
| 0,307272
| 1,25
| 0,629203
| 0,365691
| |
| 1,3
| 0,841257
| 0,455029
| 1,35
| 1,068772
| 0,542874
| |
| 1,4
| 1,384131
| 0,56232
| 1,45
| 1,665291
| 0,398036
| |
| 1,5
| 1,782167
| 0,289644
| 1,55
| 1,926989
| 0,147683
| |
| 1,6
| 1,92985
| 0,154909
| 1,65
| 2,007304
| 0,097318
| |
| 1,7
| 2,027167
| 0,092905
| 1,75
| 2,07362
| 0,075162
| |
| 1,8
| 2,10233
| 0,072751
| 1,85
| 2,138705
| 0,072866
| |
| 1,9
| 2,175195
| 0,080055
| 1,95
| 2,215223
| 0,095675
| |
|
| 2,270871
| 0,129148
| 2,05
| 2,335445
| 0,188847
|
Далі можна, як і в задачі 1, скопіювати попередні формули, наприклад у діапазон J1:O3, а потім у чарунках A3, C2, D2, F2 у $H$1 замінити 1 на 2, звідки дістанемо:
|
| J
| K
| L
| |
| x
| y
| w1
| |
|
|
| = $H$2*(2*J2+3*SIN(K2^2))
| |
| = J2 + $H$2
| = K2 + O2
| ↓
| |
| ↓
| ↓
| ↓
| |
| M
| N
| O
| |
| x1
| y1
| w2
| |
| = J2 + 0,5*$H$2
| = K2 + 0,5*L2
| = $H$2*(2*M2+3*SIN(N2^2))
| |
| ↓
| ↓
| ↓
| |
| ↓
| ↓
| ↓
|
І тоді в результаті обчислень дістанемо:
|
| J
| K
| L
| M
| N
| O
| |
| х
| у
| w1
| х1
| у1
| w2
| |
|
|
| 0,1
| 1,025
| 0,05
| 0,102875
| |
| 1,05
| 0,102875
| 0,106587
| 1,075
| 0,156169
| 0,111158
| |
| 1,1
| 0,214033
| 0,116869
| 1,125
| 0,272467
| 0,123626
| |
| 1,15
| 0,337658
| 0,132065
| 1,175
| 0,403691
| 0,141837
| |
| 1,2
| 0,479495
| 0,154184
| 1,225
| 0,556588
| 0,168229
| |
| 1,25
| 0,647724
| 0,186102
| 1,275
| 0,740775
| 0,205743
| |
| 1,3
| 0,853467
| 0,229852
| 1,325
| 0,968393
| 0,253437
| |
| 1,35
| 1,106905
| 0,276133
| 1,375
| 1,244971
| 0,287467
| |
| 1,4
| 1,394372
| 0,27966
| 1,425
| 1,534202
| 0,248822
| |
| 1,45
| 1,643194
| 0,209095
| 1,475
| 1,747742
| 0,160532
| |
| 1,5
| 1,803726
| 0,133259
| 1,525
| 1,870356
| 0,100131
| |
| 1,55
| 1,903857
| 0,085324
| 1,575
| 1,946519
| 0,067039
| |
| 1,6
| 1,970897
| 0,058542
| 1,625
| 2,000168
| 0,048914
| |
| 1,65
| 2,019811
| 0,04404
| 1,675
| 2,04183
| 0,0391
| |
| 1,7
| 2,058911
| 0,036488
| 1,725
| 2,077155
| 0,034214
| |
| 1,75
| 2,093124
| 0,033153
| 1,775
| 2,109701
| 0,032601
| |
| 1,8
| 2,125726
| 0,032805
| 1,825
| 2,142128
| 0,033646
| |
| 1,85
| 2,159372
| 0,035184
| 1,875
| 2,176964
| 0,037554
| |
| 1,9
| 2,196925
| 0,040975
| 1,925
| 2,217413
| 0,045627
| |
| 1,95
| 2,242552
| 0,052457
| 1,975
| 2,268781
| 0,061468
| |
|
| 2,30402
| 0,075872
| 2,025
| 2,341956
| 0,095061
|
Оскільки похибка на кожному кроці є систематичною, то найбільшу похибку слід очікувати у кінцевій точці 2. Тому порівняємо тепер наближені значення розв’язку задачі Коші, отримані в задачі удосконаленим методомЕйлера, саме у цій точці за допомогою наступної таблиці для подвійного перерахунку.
|
| A
| B
| C
| D
| |
| h
| y(2)
| ε
| y(2) уточн.
| |
| 0,1
| 2,270871
|
|
| |
| 0,05
| 2,30402
| 0,01105
| 2,31507
|
Тут у стовпці А крок інтегрування, у стовпці В наближені значення в точці 2, отримані у попередніх таблицях з відповідним кроком: за позначеннями формули (6) уk = 2,270871,  = 2,30402. У С17 підрахована за правилом Рунге (6) похибка ε = – = 2,30402. У С17 підрахована за правилом Рунге (6) похибка ε = –  наближення наближення  у чарунці В17 ε ≈ у чарунці В17 ε ≈  , де s – порядок точності методу, в даному разі порядок удосконаленого методу Ейлера s = 2, тобто С17 = (В17 – В16)/3. Виявляється, що і справді знайдена так точність , де s – порядок точності методу, в даному разі порядок удосконаленого методу Ейлера s = 2, тобто С17 = (В17 – В16)/3. Виявляється, що і справді знайдена так точність  приблизно дорівнює hs = (0,1)2 = 0,01. Як було зазначено у попередньому параграфі, цей підрахунок ε насправді зроблений з точністю порядку hs+1, тобто порядку (0,1)3 = 0,001. Нарешті, у чарунці D17 підраховане уточнене наближення для y(2) за формулою (7) (тобто D17 = В17 + С17), точність якого вже порядку 10-3. Ця таблиця фактично і є відповіддю задачі 2. приблизно дорівнює hs = (0,1)2 = 0,01. Як було зазначено у попередньому параграфі, цей підрахунок ε насправді зроблений з точністю порядку hs+1, тобто порядку (0,1)3 = 0,001. Нарешті, у чарунці D17 підраховане уточнене наближення для y(2) за формулою (7) (тобто D17 = В17 + С17), точність якого вже порядку 10-3. Ця таблиця фактично і є відповіддю задачі 2.
Тепер можна отримати такі ж таблиці, тобто обґрунтовані апостеріорні оцінки і за підрахунками задачі 1. Наближені значення розв’язку задачі Коші порівняємо у кінцевій точці, в даному разі 1, оскільки, саме в ній слід очікувати найбільшу похибку. Спочатку розглянемо таблицю для методу Ейлера.
|
| A
| B
| C
| D
| |
| h
| y(1)
| ε
| y(1) уточн.
| |
| 0,2
| 4,60413
|
|
| |
| 0,1
| 5,21682
| = B35 – B34
| = C35 + B35
| |
| 0,05
| 5,62838
| ↓
| ↓
| |
| 0,025
| 5,87534
| ↓
| ↓
|
Оскільки порядок точності методу Ейлера дорівнює 1, то правило Рунге, яке застосовано у формулах стовпця С набуває вигляду ε =  – уk. У стовпці D обчислюються уточнені наближення точності порядку h2. В результаті дістанемо: – уk. У стовпці D обчислюються уточнені наближення точності порядку h2. В результаті дістанемо:
|
| A
| B
| C
| D
| |
| h
| y(1)
| ε
| y(1) уточн.
| |
| 0,2
| 4,60413
|
|
| |
| 0,1
| 5,21682
| 0,6127
| 5,829521
| |
| 0,05
| 5,62838
| 0,41156
| 6,039943
| |
| 0,025
| 5,87534
| 0,24696
| 6,122296
|
Порівняння останніх наближень дає 6,122296 – 6,039943 = 0,082353, що вже значно менше похибок не уточнених наближень. Таблиця удосконаленого методу Ейлера:
|
| A
| B
| C
| D
| |
| h
| y(1)
| ε
| y(1) уточн.
| |
| 5,93258
|
|
|
| |
| 6,09164
| 0,15906
| = (B42 – B41)/3
| = C42 + B42
| |
| 6,14066
| 0,04901
| ↓
| ↓
| |
| 6,15418
| 0,01352
| ↓
| ↓
|
Тут правило Рунге має вигляд ε ≈ ( – уk)/3, як і в задачі 2 (бо порядок точності s = 2). В результаті дістанемо: – уk)/3, як і в задачі 2 (бо порядок точності s = 2). В результаті дістанемо:
|
| A
| B
| C
| D
| |
| h
| y(1)
| ε
| y(1) уточн.
| |
| 0,2
| 5,93258
|
|
| |
| 0,1
| 6,09164
| 0,053021
| 6,144665333
| |
| 0,05
| 6,14066
| 0,016338
| 6,156994667
| |
| 0,025
| 6,15418
| 0,004506
| 6,158681
|
Порівняння останніх наближень дає 6,158681 – 6,156994667 = 0,000241 – перевага удосконаленого методу Ейлера у точності результатів тут є безперечною.
Задача 3. Знайти чисельний розв’язок задачі Коші  на відрізку [0; 1] методом Рунге – Кутта другого порядку точності за формулою на відрізку [0; 1] методом Рунге – Кутта другого порядку точності за формулою  , де , де 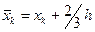 з точністю 10-4, оціненою методом кратного перерахунку. з точністю 10-4, оціненою методом кратного перерахунку.
Розв’язання. Оскільки за формулою методу q = 2, то метод Рунге – Кутта має другий порядок точності тоді і тільки тоді, коли його параметри задовольняють (5). За умовою тут α2 =  , звідки β21 = , звідки β21 =  , р2 = , р2 =  , р1 = , р1 = 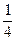 . Отже, . Отже,  , де , де  , ,  = yk + = yk +  h f (xk, yk). Спочатку задамо кроки інтегрування 0,2 0,1 0,05 0,025 у чарунках H1:H4, знайдемо чисельні розв’язки для таких кроків і оцінимо їх методом кратного перерахунку. Якщо потрібна точність не буде досягнута, то крок буде зменшено. Отже, аналогічно задачі 2, надамо чарункам таких значень: h f (xk, yk). Спочатку задамо кроки інтегрування 0,2 0,1 0,05 0,025 у чарунках H1:H4, знайдемо чисельні розв’язки для таких кроків і оцінимо їх методом кратного перерахунку. Якщо потрібна точність не буде досягнута, то крок буде зменшено. Отже, аналогічно задачі 2, надамо чарункам таких значень:
|
| A
| B
| C
| |
| x
| y
| w1
| |
|
|
| = $H$1*(SIN(0,5*A2+2*B2^2)+1,5*B2)
| |
| = A2 + $H$1
| = B2 + 1/4*C2 + 3/4*F2
| ↓
| |
| ↓
| ↓
| ↓
| |
| D
| E
| F
| |
| x1
| y1
| w2
| |
| = A2 + 2/3*$H$1
| = B2 + 2/3*C2
| = $H$1*(SIN(0,5*D2+2*E2^2)+1,5*E2)
| |
| ↓
| ↓
| ↓
| |
| ↓
| ↓
| ↓
|
В результаті дістанемо:
|
| A
| B
| C
| D
| E
| F
| |
| х
| у
| w1
| х1
| у1
| w2
| |
|
|
| 0,481859
| 0,133333
| 1,32124
| 0,315474
| |
| 0,2
| 1,35707
| 0,287412
| 0,333333
| 1,548678
| 0,270875
| |
| 0,4
| 1,632079
| 0,352446
| 0,533333
| 1,867043
| 0,723397
| |
| 0,6
| 2,262738
| 0,499223
| 0,733333
| 2,595553
| 0,969927
| |
| 0,8
| 3,114989
| 1,097962
| 0,933333
| 3,846964
| 0,958901
| |
|
| 4,108655
| 1,290827
| 1,133333
| 4,969206
| 1,429217
|
Далі, як і в попередніх задачах, скопіюємо А2:F3 у будь – які вільні від інформації діапазони, а потім у відповідних чарунках у $H$1 замінимо 1 на 2, 3 або 4. Наприклад,
|
| J
| K
| L
| |
| x
| y
| w1
| |
|
|
| = $H$2*(SIN(0,5*J2+2*K2^2)+1,5*K2)
| |
| = J2 + $H$2
| =K2+1/4*L2+3/4*O2
| ↓
| |
| ↓
| ↓
| ↓
|
|
| M
| N
| O
| |
| x1
| y1
| w2
| |
| = J2 + 2/3*$H$2
| = K2 + 2/3*L2
| = $H$2*(SIN(0,5*M2+2*N2^2)+1,5*N2)
| |
| ↓
| ↓
| ↓
|
Тоді в результаті обчислень дістанемо:
|
| J
| K
| L
| M
| N
| O
| |
| х
| у
| w1
| х1
| у1
| w2
| |
|
|
| 0,24093
| 0,066667
| 1,16062
| 0,214337
| |
| 0,1
| 1,220985
| 0,194124
| 0,166667
| 1,350401
| 0,147015
| |
| 0,2
| 1,379777
| 0,137642
| 0,266667
| 1,471539
| 0,123795
| |
| 0,3
| 1,507034
| 0,126075
| 0,366667
| 1,591085
| 0,152587
| |
| 0,4
| 1,652994
| 0,189975
| 0,466667
| 1,779644
| 0,295006
| |
| 0,5
| 1,921742
| 0,385899
| 0,566667
| 2,179008
| 0,29212
| |
| 0,6
| 2,237306
| 0,258122
| 0,666667
| 2,409388
| 0,303082
| |
| 0,7
| 2,529148
| 0,433908
| 0,766667
| 2,81842
| 0,369445
| |
| 0,8
| 2,914709
| 0,337836
| 0,866667
| 3,139933
| 0,567403
| |
| 0,9
| 3,42472
| 0,419617
| 0,966667
| 3,704465
| 0,589478
| |
|
| 3,971733
| 0,654949
| 1,066667
| 4,408366
| 0,760401
|
Так само дістанемо чисельні розв’язки для кроків h = 0,05 у чарунці H3 і h = 0,025 у H4. За цими обрахунками створимо наступну електронну таблицю кратного перерахунку. Як і вище, оцінку похибки будемо проводити у кінцевій точці, в даному разі 1, оскільки саме в ній слід очікувати найбільшу похибку.
|
| H
| I
| J
| K
| L
| |
| № перерахунку
|
|
| |
| h
| y(1)
| ε
| y(1)
| ε
| |
| 0,2
| 4,108655
|
|
|
| |
| 0,1
| 3,971733
| = 1/3*(I37–I36)
| = I37+J37
|
| |
| 0,05
| 4,056332
| ↓
| ↓
| = 1/7*(K38–K37)
| |
| 0,025
| 4,051298
| ↓
| ↓
| ↓
|
Тут у стовпці H крок інтегрування, у стовпці I наближені значення в точці 1, отримані при попередніх підрахунках з відповідним кроком, у стовпці J похибка ε, підрахована за правилом Рунге (6) ε ≈  , де s – порядок точності методу. В даному разі 2s – 1 = 3, бо s = 2. На цьому закінчився перший (подвійний) перерахунок. У стовпці К знаходимо уточнені наближення порядку точності 3 за формулою (7), у стовпці L їх оцінки ε знову за правилом Рунге ε ≈ , де s – порядок точності методу. В даному разі 2s – 1 = 3, бо s = 2. На цьому закінчився перший (подвійний) перерахунок. У стовпці К знаходимо уточнені наближення порядку точності 3 за формулою (7), у стовпці L їх оцінки ε знову за правилом Рунге ε ≈  , але тепер 2s – 1 = 7, бо s = 3. У сукупності це другий (подвійний) перерахунок. Далі аналогічно проводимо третій перерахунок: із зростанням номеру перерахунку N на одиницю порядок точності методу s завжди теж зростає на одиницю, отже тут s = 4, 2s – 1 = 15: , але тепер 2s – 1 = 7, бо s = 3. У сукупності це другий (подвійний) перерахунок. Далі аналогічно проводимо третій перерахунок: із зростанням номеру перерахунку N на одиницю порядок точності методу s завжди теж зростає на одиницю, отже тут s = 4, 2s – 1 = 15:
|
| M
| N
| O
| P
| |
|
|
| |
| y(1)
| ε
| y(1)
| ε
| |
|
|
|
|
| |
|
|
|
|
| |
| = K38 + L38
|
|
|
| |
| ↓
| = 1/15*(M39 – M38)
| = M39 + N39
|
|
В результаті отримаємо таку трикутну таблицю (матрицю):
|
| H
| I
| J
| K
| L
| M
| N
| O
| |
| №
|
|
|
|
| |
| h
| y(1)
| ε
| y(1)
| ε
| y(1)
| ε
| y(1)
| |
| 0,2
| 4,108655
|
|
|
|
|
|
| |
| 0,1
| 3,971733
| -0,04564
| 3,926093
|
|
|
|
| |
| 0,05
| 4,056332
| 0,0282
| 4,084532
| 0,022634
| 4,107166
|
|
| |
| 0,025
| 4,051298
| -0,00168
| 4,04962
| -0,00499
| 4,044633
| -0,00417
| 4,040464
|
Згідно з отриманими апостеріорними оцінками тут всі наближення мають якнайбільше три значущих цифри, що є недостатньою точністю за умовою задачі. Отже, знайдемо чисельний розв’язок даної задачі Коші з кроком інтегрування h = 0,0125 і додамо до таблиці кратного перерахунку отримане значення у(1). За підрахунками:
|
| H
| I
| J
| K
| L
| M
| |
| х
| у
| w1
| х1
| у1
| w2
| |
|
|
| 0,030116
| 0,008333
| 1,020077
| 0,030008
| |
| 0,0125
| 1,030035
| 0,029921
| 0,020833
| 1,049983
| 0,029679
| |
| 0,025
| 1,059775
| 0,029528
| 0,033333
| 1,07946
| 0,029158
| |
| 0,0375
| 1,089026
| 0,028948
| 0,045833
| 1,108324
| 0,028464
| |
| 0,05
| 1,117611
| 0,028203
| 0,058333
| 1,136412
| 0,027622
| |
| 0,0625
| 1,145378
| 0,027321
| 0,070833
| 1,163592
| 0,026665
| |
| 0,075
| 1,172207
| 0,026335
| 0,083333
| 1,189764
| 0,025628
| |
| 0,0875
| 1,198012
| 0,025281
| 0,095833
| 1,214866
| 0,024546
| |
| 0,1
| 1,222742
| 0,024192
| 0,108333
| 1,23887
| 0,023452
| ……………………………………………………………………
|
| 0,9
| 3,493643
| 0,062152
| 0,908333
| 3,535077
| 0,070155
| |
| 0,9125
| 3,561797
| 0,074801
| 0,920833
| 3,611664
| 0,080069
| |
| 0,925
| 3,640549
| 0,08032
| 0,933333
| 3,694096
| 0,075421
| |
| 0,9375
| 3,717195
| 0,071818
| 0,945833
| 3,765074
| 0,06406
| |
| 0,95
| 3,783194
| 0,061746
| 0,958333
| 3,824359
| 0,059289
| |
| 0,9625
| 3,843097
| 0,059749
| 0,970833
| 3,88293
| 0,064048
| |
| 0,975
| 3,90607
| 0,068214
| 0,983333
| 3,951547
| 0,077847
| |
| 0,9875
| 3,981509
| 0,083468
| 0,995833
| 4,037155
| 0,088123
| |
|
| 4,068469
| 0,086471
| 1,008333
| 4,126116
| 0,077411
|
Отже, достатньо занести отримане значення у(1) = 4,068469 у чарунку I40 поряд з відповідним значенням кроку h = 0,0125 у чарунці H40, решту формул у стовпцях J:O можна просто скопіювати:
|
| H
| I
| J
| K
| L
| M
| N
| O
| P
| Q
| R
| |
| №
|
|
|
|
|
| |
| h
| y(1)
| ε
| y(1)
| ε
| y(1)
| ε
| y(1)
| ε
| y(1)
| ε
| |
| 0,2
| 4,108655
|
|
|
|
|
|
|
|
|
| |
| 0,1
| 3,971733
| *
| *
|
|
|
|
|
|
|
| |
| 0,05
| 4,056332
| ↓
| ↓
| *
| *
|
|
|
|
|
| |
| 0,025
| 4,051298
| ↓
| ↓
| ↓
| ↓
| *
| *
|
|
|
| |
| 0,0125
| 4,068469
| ↓
| ↓
| ↓
| ↓
| ↓
| ↓
| =(O40-O39)/31
| =O40+P40
|
|
Тут символ * означає, що у відповідній чарунці знаходиться та ж сама формула, що й у попередній таблиці. Для N = 4 s = 5, 2s – 1 = 31, тому Р40 = (O40 – O39)/31. В результаті отримаємо таку трикутну таблицю:
|
| H
| I
| J
| K
| L
| |
| №
|
|
| |
| h
| y(1)
| ε
| y(1)
| ε
| |
| 0,2
| 4,108655
|
|
|
| |
| 0,1
| 3,971733
| -0,04564
| 3,926093
|
| |
| 0,05
| 4,056332
| 0,0282
| 4,084532
| 0,022634
| |
| 0,025
| 4,051298
| -0,00168
| 4,04962
| -0,00499
| |
| 0,0125
| 4,068469
| 0,005724
| 4,074192
| 0,00351
| |
| M
| N
| O
| P
| Q
| |
|
|
|
| |
| y(1)
| ε
| y(1)
| ε
| y(1)
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
| 4,107166
|
|
|
|
| |
| 4,044633
| -0,00417
| 4,040464
|
|
| |
| 4,077703
| 0,002205
| 4,079907
| 0,001272
| 4,08118
|
На четвертому перерахунку наближення досягло вже чотирьох значущих цифр, проте точності 10-4, яку вимагає умова задачі, ще не досягнуто. Тому знайдемо ще й чисельний розв’язок даної задачі Коші з кроком інтегрування h = 0,0125 і отримане значення у(1) додамо до таблиці кратного перерахунку. За підрахунками:
|
| A
| B
| C
| D
| E
| F
| |
| х
| у
| w1
| х1
| у1
| w2
| |
| 0,95
| 3,786632
| 0,030691
| 0,954167
| 3,807093
| 0,029888
| |
| 0,95625
| 3,816721
| 0,0297
| 0,960417
| 3,83652
| 0,029734
| |
| 0,9625
| 3,846446
| 0,02997
| 0,966667
| 3,866426
| 0,030876
| |
| 0,96875
| 3,877096
| 0,03158
| 0,972917
| 3,898149
| 0,033341
| |
| 0,975
| 3,909996
| 0,0345
| 0,979167
| 3,932996
| 0,036938
| |
| 0,98125
| 3,946325
| 0,038371
| 0,985417
| 3,971905
| 0,040913
| |
| 0,9875
| 3,986602
| 0,042126
| 0,991667
| 4,014686
| 0,043685
| |
| 0,99375
| 4,029897
| 0,04403
| 0,997917
| 4,05925
| 0,043635
| |
|
| 4,073631
| 0,042962
| 1,004167
| 4,102272
| 0,040882
|
Отже, отримане значення у(1) = 4,068469 заносимо до таблиці кратного перерахунку. В результаті отримаємо таку таблицю:
|
| H
| I
| J
| K
| L
| |
| №
|
|
| |
| h
| y(1)
| ε
| y(1)
| ε
| |
| 0,2
| 4,108655
|
|
|
| |
| 0,1
| 3,971733
| -0,04564
| 3,926093
|
| |
| 0,05
| 4,056332
| 0,0282
| 4,084532
| 0,022634
| |
| 0,025
| 4,051298
| -0,00168
| 4,04962
| -0,00499
| |
| 0,0125
| 4,068469
| 0,005724
| 4,074192
| 0,00351
| |
| 0,00625
| 4,073631
| 0,001721
| 4,075352
| 0,000166
|
|
| M
| N
| O
| P
| Q
| R
| S
| |
|
|
|
|
| |
| y(1)
| ε
| y(1)
| ε
| y(1)
| ε
| y(1)
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
| 4,107166
|
|
|
|
|
|
| |
| 4,044633
| -0,00417
| 4,040464
|
|
|
|
| |
| 4,077703
| 0,002205
| 4,079907
| 0,001272
| 4,08118
|
|
| |
| 4,075518
| -0,00015
| 4,075372
| -0,00015
| 4,075226
| -9,45052E-05
| 4,075131
|
Як бачимо, тепер необхідна точність досягнута вже на другому перерахунку. Проте, як було доведено і видно з формули (13), отримані оцінки самі є наближеними числами і тому не можна виключати, що при наступному перерахунку оцінка зросте. У такому разі отримана на попередньому перерахунку величина не є достовірною. У даному прикладі цього не сталося, отже значення 4,075226 або 4,075131 можна вважати отриманими з точністю 10-4, з чотирма вірними значущими цифрами.
|



 на відрізку [1; 2] з кроками інтегрування h = 0,1 0,05 методом Рунге – Кутта другого порядку точності по формулам
на відрізку [1; 2] з кроками інтегрування h = 0,1 0,05 методом Рунге – Кутта другого порядку точності по формулам  , де
, де  , і оцінити похибку отриманого розв’язку методом подвійного перерахунку.
, і оцінити похибку отриманого розв’язку методом подвійного перерахунку. , звідки β21 =
, звідки β21 =  , де
, де  = yk +
= yk +  ,
,  = 2,30402. У С17 підрахована за правилом Рунге (6) похибка ε = –
= 2,30402. У С17 підрахована за правилом Рунге (6) похибка ε = –  наближення
наближення  , де s – порядок точності методу, в даному разі порядок удосконаленого методу Ейлера s = 2, тобто С17 = (В17 – В16)/3. Виявляється, що і справді знайдена так точність
, де s – порядок точності методу, в даному разі порядок удосконаленого методу Ейлера s = 2, тобто С17 = (В17 – В16)/3. Виявляється, що і справді знайдена так точність  на відрізку [0; 1] методом Рунге – Кутта другого порядку точності за формулою
на відрізку [0; 1] методом Рунге – Кутта другого порядку точності за формулою 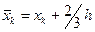 з точністю 10-4, оціненою методом кратного перерахунку.
з точністю 10-4, оціненою методом кратного перерахунку. , звідки β21 =
, звідки β21 =  , р1 =
, р1 = 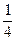 . Отже,
. Отже,  , де
, де  ,
, 


