
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 1. Методи обчислень: предмет, основні поняття та застосуванняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Предмет і застосування Методи обчислень – це алгоритми знаходження чисельних (доведених до числових відповідей) розв’язків типових математичних задач. А саме рівнянь (диференціальних в тому числі), систем рівнянь і нерівностей, задач аналізу (диференціювання, інтегрування, наближення функцій), задач оптимізації тощо. Головна мета цих алгоритмів – отримати наближені розв’язки з заздалегідь заданою точністю та найшвидше. Для рівняння f (x) = 0, де f (x) – многочлен степеня n > 4 не існує універсальних аналітичних методів для отримання точних значень коренів. Їх нема навіть для рівняння x2 + sin x = 0, та й практично для будь – якого довільно написаного рівняння. З іншого боку при застосуванні як правило байдуже чи є корінь точним чи він отриманий з прийнятною точністю. Тому вкрай важливо мати алгоритми знаходження наближених розв’язків, які б сходились до точного із зростанням числа кроків алгоритму. Такі методи називають ітераційними. Назви деяких з таких методів – Ньютона, Ейлера, Лобачевського, Гаусса, Ерміта – свідчать про те, що їх розробкою займались найвидатніші вчені свого часу. Після виконання складних обчислень Дж. Адамс у 1845 році та У. Левер’є у 1846 незалежно один від одного дійшли висновку про існування невідомої досі планети і вказали її розміщення. За розрахунками Левер’є астроном І. Галле знайшов цю планету, її назвали Нептуном. Аналогічно на “кінчику пера” П. Ловелл у 1930 р. передбачив існування дев’ятої планети сонячної системи – Плутона. Але такі яскраві події були унікальними, до того ж стосувались вони лише найбільш математизованих наук – фізики, механіки, астрономії: надто трудомісткі були обчислення. Звичайно, принципово можна знайти розв’язок системи лінійних рівнянь, однак вручну це неабияке випробування уже для системи десяти рівнянь з десятьма невідомими. Сучасний бурхливий розвиток комп’ютерної техніки докорінно змінив ці можливості. (Тут доречно зауважити, що за два століття промислової революції, викликаної винаходом парового двигуна, швидкість пересування зросла з 6 км/год. до швидкості космонавта 30000 км/год. тобто у 5000 разів. За перші ж 30 років інформаційної революції швидкість виконання арифметичних операцій зросла з 0,1 операцій у секунду при обчисленнях вручну до 3000000, тобто приблизно у (5000)2 разів). Завдяки кардинальному зростанню можливостей обчислень якісно зросли й можливості науки взагалі.
Річ в тому, що необхідною передумовою будь – якого використання методів обчислень є створення математичної моделі досліджуваного об’єкта чи явища, тобто опис його мовою математичних структур. Метою ж обчислень неодмінно є отримання таких висновків, які можна було б віднести до реального об’єкту. Але саме цей цикл: створення математичної моделі → обчислення → порівняння з реальним об’єктом – і є насправді єдиний досі метод дослідження світу фундаментальними науками, задум якого належить І. Ньютону. Обчислення – центральний пункт цього циклу, якісне зростання його можливостей відкрило змогу віднині вивчати будь – які математичні моделі, а не лише вузькі спеціальні класи, як це насправді було до того. Відтепер почалась математизація хімії, економіки, геології, психології, медицини, багатьох галузей техніки. Розвиток економіки, атомної енергетики, космічної техніки був би просто неможливим без застосування комп’ютерів та методів обчислень. Повідомлення про результати обчислень провідними фінансовими аналітичними центрами або ж повідомлення про розходження між цими результатами та реальними статистичними даними викликає негайну реакцію на всіх біржах світу. Основною метою вивчення методів обчислень безперечно є їх подальше застосування. Цілком технологічний цикл використання методів обчислень виглядає так: 1) побудова математичної моделі задачі → 2) розробка методу обчислень → 3) програмування → 4) тестування → 5) аналіз результатів → 6) застосування. 1) Математична модель задачі – це математична задача, до розв’язування якої зводиться поставлена задача з даної конкретної галузі. Формулювання математичної моделі – це не менш складна проблема, ніж її розв’язування. Не можна сподіватись, що це зроблять фахівці тієї галузі, звідки походить поставлена задача: як правило, це результат їх зусиль, спільних з тими, хто має спеціальну математичну освіту. Вміння знайти, сформулювати математичну модель – неодмінна мета учбового процесу. 2) Не менш важливо вміти знайти або розробити найкращий метод розв’язування математичної моделі. Оцінюючи якість (іншими словами ефективність) методу, окрім спроможності отримати наближені розв’язки з заздалегідь заданою точністю найшвидше, враховують його універсальність (можливість застосування у багатьох задачах), економічність (витрати часу, грошей та пам’яті комп’ютера), простоту організації обчислювального процесу та контролю точності, стійкість результатів обчислень відносно похибок даних.
Не варто розраховувати, що вдасться завжди знайти готовий метод розв’язання будь – якої реальної задачі: насправді їх різноманітність є практично необмеженою. 3) Сучасні мови програмування безпосередньо пов’язані з пакетами прикладних програм, призначених для розв’язування певного класу задач. Знання цих пакетів, вміння їх застосувати значно спрощує процес програмування обчислювальних алгоритмів. 4) Оскільки запрограмована математична модель є дублікатом реального об’єкта у комп’ютері, а тестування є аналогом експерименту з цим об’єктом, то його й називають обчислювальним (або математичним) експериментом. Головна мета – тестування таких даних, щоб можна було надійно судити про достовірність розв’язків задачі. Разом з тим за допомогою обчислювального експерименту передбачається поведінка досліджуваного об’єкта в умовах, де натурні експерименти ще не проводились або й зовсім неможливі. Тестування – це копітка та трудомістка дослідницька робота, вміння проводити її є вкрай важливим. 5) На основі тестування проводиться аналіз як відповідності математичної моделі реальному об’єкту, так і ефективності методу. Саме такий, заснований на вже проведених розрахунках (тобто апостеріорний) аналіз найчастіше застосовується на практиці: існує строк виконання, тож дослідження в стилі чистої математики у більшості випадків тут неможливі. Описаний тут технологічний процес є циклом: якщо результати задовільні, то програму передають замовнику для застосування; якщо ні, то цикл повторюється.
Основні поняття Похибки наближень. Означення 1. Нехай а – точне значення деякої величини, а* - відоме наближення до нього. Абсолютною похибкою (погрішністю) наближення а* називають таку величину Δ(а*), для якої Відносну погрішність часто виражають у відсотках. Звичайні позначення: а = а* Так, наприклад, запис а = 1,123 1,123 – 0,004 Означення 2. Значущими цифрами числа називають всі цифри у його запису, починаючи з першого ненульового зліва. Значущу цифру наближення називають вірною, якщо його абсолютна похибка не перевищує одиниці розряду, що відповідає цій цифрі. Наприклад, у чисел 0.0 3045 і 0,0 3045000 значущими цифрами є підкреслені. У першому випадку число значущих цифр дорівнює 4, у другому 7. У числа а* = 0,0 304 5 вірні підкреслені числа, якщо Δ(а*) = 0,00003; так само у числа а* = 0,0 30450 00, якщо Δ(а*) = 0,0000007.
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 707; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.71.40 (0.012 с.) |

 . Відносною похибкою (погрішністю) називають таку величину δ(а*), що
. Відносною похибкою (погрішністю) називають таку величину δ(а*), що  .
. Δ(а*), а = а*(1
Δ(а*), а = а*(1 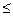 а
а 


