
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Канонічна форма задачі лінійного програмування. Опорні розв’язкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте За означенням 2 задача лінійного програмування поставлена, якщо задані 1) лінійна цільова функція f = 2) система обмежень
3) визначено, до якого типу відноситься дана задача – максимізації або мінімізації. Зазначимо, що нерівність f =
xj ≥ 0 (j = 1, 2, …, n1 ≤ n).
Зокрема, якщо m1 = 0, то система обмежень складається лише з нерівностей; якщо m1 = m, то з рівнянь, окрім останньої строки. Означення 4. Матриця А системи (1) вимірності m × n
називається матрицею умов, стовпці А1, А2, …, Аn цієї матриці – векторами умов,
а вектор В називається вектором обмежень задачі (1). Означення 5. Задача лінійного програмування має канонічну форму, якщо всі її змінні невід’ємні, а всі інші умови системи обмежень – рівняння (тобто у (1) m1 = m, n1 = n). Отже, в канонічній формі задача лінійного програмування має вид: f =
xj ≥ 0 (j = 1, 2, …, n). (2)
У векторній формі систему обмежень задачі (2) можна записати так:
де А1, А2, …, Аn – вектори умов, а В вектор обмежень цієї задачі. Будь – яку задачу лінійного програмування можна звести до канонічної форми. Справді, кожну змінну xj задачі (1) (n1 ≤ j ≤ n) замінимо на різницю yj – zj двох нових невід’ємних змінних yj і zj. Крім того, у нерівностях Приклад. Звести до канонічної задачу: знайти мінімум лінійної функції f = 2х1 + 3х2 + х3 за обмежень
Розв’язання. Введемо в першу нерівність системи змінну х4 ≥ 0, а в третю – х5, х5 ≥ 0:
Змінна х2 не підпорядкована умові невід’ємності. Тому замінимо цю змінну різницею х2 = х6 – х7, де х6 ≥ 0, х7 ≥ 0. Підставивши значення х2 у цільову функцію і систему обмежень, дістанемо задачу у канонічній формі:
f = 2х1 + 3х6 – 3х7 + х3 (min)
Систему обмежень задачі лінійного програмування в канонічній формі можна розв’язати методом Гаусса, як і будь – яку систему лінійних рівнянь. Якщо вона сумісна, то має або єдиний розв’язок або нескінченну множину розв’язків, кожен з яких отримується із загального в результаті фіксації вільних (неосновних) змінних. Розв’язок є допустимим, якщо всі його координати невід’ємні. Означення 6. 1) Опорним розв’язком задачі лінійного програмування у канонічній формі називають такий допустимий розв’язок її системи обмежень, у якому всі вільні змінні дорівнюють нулю. 2) Опорний розв’язок називають невиродженим, якщо всі його основні змінні додатні, в противному разі опорний розв’язок називають виродженим. Традиційним є таке еквівалентне Означення 6′. Опорним розв’язком задачі (2) називається її допустимий розв’язок, якщо вектори умов з номерами його додатних координат утворюють лінійно незалежну систему векторів. Справді, як показано у розділі, набір змінних системи лінійних рівнянь буде набором основних змінних загального розв’язку за одної умови: набір вектор – стовпців матриці цієї системи з номерами цих змінних утворює максимальну лінійно незалежну систему, тобто базис вектор – стовпців. Звідси 6 → 6′: якщо всі вільні змінні у розв’язку дорівнюють нулю, то всі змінні з додатними значеннями основні, а тому їх вектори умов утворюють лінійно незалежну систему. Зворотно 6′ → 6: якщо вектори умов з номерами додатних координат розв’язку утворюють лінійно незалежну систему, то її можна розширити до базису, відповідно розширити набір змінних і обрати змінні цього набору, як основні. Тоді у якості вільних залишаються тільки змінні із значенням нуль. Звідси Означення 7. Базисом опорного розв’язку називають такий базис векторів умов, який містить всі вектори умов, що відповідають додатним координатам цього розв’язку. Отже, довільний опорний розв’язок має базис. У невиродженого опорного розв’язку він тільки один, його складають всі вектори умов, що відповідають додатним координатам цього розв’язку; вироджений може мати декілька базисів. Приклад. В задачі лінійного програмування у канонічній формі f = 3х1 + 4х2 – х3 + х4 (min)
α1 = (0;0;1/2;5/2) і α2 = (1;0;1;1) є допустимими розв’язками. Водночас вектори умов А3 = Щоби знайти опорний розв’язок достатньо вибрати деякий базис векторів умов задачі так, щоби вектор обмежень В розкладався по ньому з невід’ємними коефіцієнтами. Якщо При розв’язанні конкретних задач ми будемо користуватись означенням 6. Воно зручно також для встановлення геометричного змісту опорного розв’язку. А саме зазначимо, що опорний розв’язок є крайньою точкою опуклої множини Ω допустимих розв’язків задачі лінійного програмування. Справді, нехай опорний розв’язок х є опуклою комбінацією допустимих розв’язків y, z: х = λ ∙ y + μ ∙ z, де у,z є Ω, λ, μ ≥ 0, λ + μ = 1. Оскільки всі координати векторів y і z невід’ємні, а вільні координати вектора х дорівнюють нулю, то ці координати дорівнюють нулю також у векторів y і z. Але тоді вектори y і z є частковими розв’язками тої ж системи лінійних рівнянь, що й х, з тими ж значеннями вільних змінних, звідки х = y = z. Згідно з означенням 3 це й означає, що х є крайньою точкою множини допустимих розв’язків Ω. З іншого боку легко зрозуміти, що будь – який допустимий розв’язок х, що має додатну вільну координату буде опуклою комбінацією деяких допустимих розв’язків y, z ≠ х, тобто лише опорні розв’язки є крайніми точками Ω. Отже, враховуючи висновки попереднього параграфа, отримаємо Висновки. 1. Опорні розв’язки задачі лінійного програмування у канонічній формі і тільки вони є вершинами множини Ω допустимих розв’язків, яка є многогранником у Rn із скінченим числом вершин. Звідси 2. Якщо множина Ω не пуста, то задача лінійного програмування у канонічній формі має опорний розв’язок, кількість опорних розв’язків скінченна. 3. Множина оптимальних розв’язків задачі лінійного програмування у канонічній формі (якщо вони існують) є теж опуклим многогранником, вершинами якого є деякі опорні розв’язки. Отже, довільний оптимальний розв’язок є опуклою комбінацією деяких оптимальних опорних розв’язків. На цих висновках оснований симплекс – метод – найбільш поширений алгебраїчний метод розв’язування задач лінійного програмування (симплекс – синонім многогранника). Якщо коротко, то суть його в тому, що достатньо шукати лише опорні розв’язки, а їх скінченна кількість і їх можна знайти методом Гаусса.
§4. Симплекс – таблиця Основним об’єктом у симплекс – методі є симплекс – таблиця. Фактично це розширена матриця системи обмежень задачі лінійного програмування у канонічній формі, до якої додано рівняння нульового рівня цільової функції f = 0. Формально кажучи, для задачі
f =
xj ≥ 0 (j = 1, 2, …, n)
симплекс – таблицею називають таку таблицю:
Нехай α = (0;…;
У стовпці вільних членів b системи лінійних рівнянь у відповідних рядках отримані значення опорного розв’язку: якщо всі вільні змінні дорівнюють нулю, то звідси
де Означення 8. Отриманутаблицю називають симплекс – таблицею, приведеною до базису Зміст оцінок δj у тому, що це коефіцієнти цільової функції, вираженої через вільні змінні опорного розв’язку α. Справді, δj = с j f = = Теорема 1. (Ознака оптимальності). 1) Якщо всі оцінки деякого базису опорного розв’язку α недодатні, то α є оптимальним розв’язком задачі лінійного програмування у канонічній формі (3). 2) Для оптимального опорного розв’язку задачі лінійного програмування у канонічній формі (3) завжди існує базис, всі оцінки якого недодатні. Справді, нехай δj – оцінки деякого базису опорного розв’язку α, звідки f = Навпаки, нехай α – невироджений опорний розв’язок (а у невиродженого опорного розв’язку базис тільки один). Нехай існує така оцінка δp базису опорного розв’язку α, що δp > 0. Для деякого θ > 0 покладемо Теорема 2. (Умова необмеженості цільової функції). Нехай симплекс – таблиця задачі лінійного програмування приведена до базису деякого опорного розв’язку α. Якщо серед оцінок цього базису існує додатна δs > 0, а решта елементів s – го стовпця недодатні, то цільова функція не обмежена зверху. Якщо ж існує оцінка δs < 0, а решта елементів s – го стовпця невід’ємні, то цільова функція не обмежена знизу. Справді, для довільного θ > 0 покладемо Приклад. Розглянемо опорний розв’язок α = (1;0;0;0) задачі f = – 10x1 + x2 – 9x3 + 6x4 (min),
Змінивши знак у цільової функції, отримаємо f = 10x1 – x2 + 9x3 – 6x4 (mах). Відповідна симплекс – таблиця:
Приведемо симплекс – таблицю цієї задачі до базису А1, А2 опорного розв’язку α:
Серед оцінок є додатна δ3 > 0. Отже, на цьому етапі не можна стверджувати, що α є оптимальним розв’язком. З іншого боку розглянемо базис А1, А3 того ж опорного розв’язку α. Так само приведемо симплекс – таблицю до цього базису:
Всі оцінки недодатні. Отже, α є оптимальним розв’язком цієї задачі, вектори А1 і А3 складають його базис.
Симплекс – метод. На цих теоремах і ґрунтується симплекс – метод. Він дає спосіб на кожному кроці від неоптимального згідно з теоремою 1 опорного розв’язку перейти до наступного, ближчого до оптимального, ніж попередній, тобто поліпшити його. Тому симплекс – метод називають ще методом послідовного поліпшення опорного розв’язку. Цей алгоритм закінчує роботу, якщо встановлюється оптимальність отриманого опорного розв’язку згідно з теоремою 1 або ж відсутність оптимального розв’язку згідно з теоремою 2. Пояснімо його спочатку на конкретному прикладі. Приклад. Для виготовлення продукції використовують три вида сировини і чотири способи виробництва. Запаси сировини, її витрати на одиницю продукції та кількість виготовляємої продукції по кожному способу (за годину роботи) наведені у таблиці.
Треба знайти план виробництва, за яким буде отримана найбільша кількість продукції. Це приклад задачі планування виробництва, розглянутий в §1. Як там показано, позначивши через хj час використання j – го способу виробництва (j = 1,2,3,4), дістанемо таку задачу лінійного програмування. f = 12x1 + 7x2 + 18x3 + 10x4 (max),
Ввівши нові змінні х5, х6, х7, зведемо цю задачу до канонічної: f = 12x1 + 7x2 + 18x3 + 10x4 (max)
Складемо її симплекс – таблицю:
Симплекс – таблиця виявляється приведеною до базису А5, А6, А7 опорного розв’язку α1 = (0; 0; 0; 0; 18; 30; 40), f (α1) = 0. Це видно з того, що матриця такого розв’язку на стовпцях змінних х5, х6, х7 є діагональною і отже відповідна система лінійних рівнянь у звичайній формі загального розв’язку має вигляд:
Отже, змінні х5, х6, х7 є основними, решта вільні. Вільні змінні опорного розв’язку х1 = х2 = х3 = х4 = 0, звідси х5 = 18, х6 = 30, х7 = 40. Оцінки основних змінних дорівнюють нулю, отже цільова функція виражена через вільні змінні опорного розв’язку α1, f = 0. Серед оцінок базису є додатні, тож α1 не є оптимальним згідно з ознакою оптимальності (теорема 1). Процедура його поліпшення, до розгляду якої ми переходимо, і є кроком симплекс – методу. Виберемо будь – яку з додатних оцінок, скажімо δ1 = 12. (Найчастіше вибирають найбільшу, але це не обов’язково). Тим самим обрані змінна х1 і стовпець 1 симплекс – таблиці (з номером оцінки). Якщо знайти новий опорний розв’язок α2, у якому змінна х1 стане основною (замість вільної у α1), а тим самим додатною, то й значення цільової функції f = 12x1 + 7x2 + 18x3 + 10x4 збільшиться на 12x1 і стане додатним. Отже f (α2) ≥ f (α1), такий α2 ближче за α1 до оптимального. Фактично процедура знаходження α2 така. Розглянемо відношення вільних членів до відповідних елементів обраного стовпця (в даному прикладі це 18/1, 30/1, 40/1) і серед них виберемо найменше. Тим самим обрані рядок (у прикладі теж перший) і елемент на перетині обраних рядка і стовпця (тут а11 = 1). Насправді це обрано місце, де елемент стовпця змінної х1 у симплекс – таблиці нового опорного розв’язку α2 буде дорівнювати одиниці, решта елементів повинна дорівнювати нулю, оскільки для α2 змінна х1 стане основною, а її стовпець частиною діагональної матриці. Обрані елемент, рядок і стовпець називають ведучими для наступного жорданова перетворення: як і у методі Гаусса, операціями над рядками симплекс – таблиці (тобто матриці) ведучий елемент роблять одиницею, а решту елементів ведучого стовпця нулями. У цьому прикладі вже а11 = 1, тож достатньо відняти перший рядок від другого і третього, від останнього рядка треба відняти перший, помножений на 12. В результаті отримаємо таку симплекс – таблицю:
В результаті змінна х1 стала основною (що і було метою перетворення), натомість змінна х5 стала вільною, отже новий набор основних змінних – це х1, х6, х7 ; новий загальний розв’язок, відповідний симплекс – таблиці, має вигляд
отже новий опорний розв’язок α2 = (18; 0; 0; 0; 0; 12; 22); цільова функція, виражена через новий набір вільних змінних має вигляд f = 216 – 17x2 + 6x3 + 10x4 – 12x5; f (α2) = 216 > f (α1) = 0. На цьому завершується перший крок симплекс – метода. Зазначимо, що у цій процедурі обирався лише рядок (по критерію мінімуму відношень), все інше випливало з цього автоматично. Спробуємо у якості ведучого обрати рядок 2 замість рядка 1. Тоді ведучий елемент а21 = 1, отже для жорданова перетворення достатньо відняти другий рядок від першого і третього, від четвертого рядка треба відняти другий, помножений на 12. Маємо:
В результаті набір основних змінних: х1, х5, х7 ; опорний розв’язок (30; 0; 0; 0;–12; 0;10; 0). Він не є допустимим, оскільки х5 = – 12. Так само станеться, якщо обрати рядок 3 у якості ведучого. Зміст критерію мінімуму відношень у тому, що лише за таким вибором новий опорний розв’язок виявиться допустимим, тому його називають умовою допустимості. Це буде доведено при розгляді симплекс – метода у загальному вигляді, зараз продовжимо розгляд приклада. Другий крок. У симплекс – таблиці, отриманій на першому кроці, залишилось дві додатні оцінки: 6 і 10. Обираємо серед них більшу: як ми бачили, ця оцінка є множником для величини збільшення цільової функції на кроці, тож можна сподіватись, що в такому разі і ця величина виявиться найбільшою (хоч насправді це не завжди так). Тим самим обрані змінна х4 і відповідний стовпець симплекс – таблиці. Якщо знайти новий опорний розв’язок α3, у якому змінна х4 стане основною (замість вільної у α2), а тим самим додатною, то й значення цільової функції f = 216 – 17x2 + 6x3 + 10x4 – 12x5 збільшиться, на 10х4. Отже f (α3) ≥ f (α2), такий α3 поліпшить α2 . Як і на першому кроці, розглянемо відношення вільних членів до відповідних елементів обраного стовпця: 12/1, 22/2; виберемо серед них найменше 22/2 (лише додатні елементи стовпця у розгляді: доведення умови допустимості далі при розгляді симплекс – методу у загальному вигляді). Тим самим обрані ведучий рядок 3 і ведучий елемент а34 = 2 для жорданова перетворення. Отже поділимо рядок 3 на 2, а отриманий рядок віднімемо від другого та помноживши на 10 від четвертого. Маємо:
В результаті змінна х4 стала основною, змінна х7 стала вільною, новий набір основних змінних – це х1, х3, х6 ; отже новий опорний розв’язок α3 = (18; 0; 0; 11; 0; 1; 0), цільова функція, виражена через новий набір вільних змінних має вигляд f = 326 – 22х2 – 4х4 – 7х5 – 5х7, f (α3) = 326 > f (α2) = 216. Нарешті всі оцінки не додатні. Згідно з теоремою 1 на цьому симплекс – метод завершує роботу. Якщо знайти новий опорний розв’язок, у якому будь – яка вільна змінна х2, х4, х5 або х7 стане основною (замість вільної у α3), а тим самим додатною, то значення цільової функції f зменшиться. Отже α3 є оптимальним розв’язком задачі лінійного програмування у канонічній формі. Щодо початкової задачі, то відкидаємо три останні додані змінні. Відповідь її така. Для виготовлення найбільшої кількості продукції при даних запасах сировини необхідно застосовувати на протязі 18 годин перший спосіб виробництва та на протязі 11 годин – четвертий. В результаті буде виготовлено 326 одиниць продукції. Нарешті сформулюємо симплекс – метод у загальному вигляді. 1. Звести задачу лінійного програмування до канонічної форми (далі будемо вважати, що задача дана у формі (3)). Записати її симплекс – таблицю. 2. Знайти деякий початковий опорний розв’язок задачі (3), привести симплекс – таблицю до базису цього розв’язку, зокрема обчислити оцінки δj всіх його основних змінних. 3. Згідно з ознакою оптимальності (теорема 1), якщо всі оцінки δj ≤ 0, то цей розв’язок є оптимальним і на цьому симплекс – метод завершує роботу. Якщо ж серед оцінок є додатні, то виконується процедура його поліпшення, яка і є кроком симплекс – метода. 1) Вибираємо довільну додатну оцінку, скажімо δs. Тим самим обрані змінна хs і стовпець з номером s симплекс – таблиці. 2) Якщо всі елементи стовпця s, окрім самої оцінки δs > 0, недодатні, то цільова функція не обмежена зверху (умова необмеженості цільової функції, теорема 2), тобто оптимального розв’язку задачі (3) не існує і на цьому симплекс – метод припиняє роботу. 3) Якщо у стовпці s є додатні елементи, то серед відношень вільних членів di до відповідних додатних елементів ais стовпця s обираємо найменше Θ = для деякого рядка з номером k. Умову (4) на рядок k називають умовою допустимості. 4) На перетині обраних рядка k і стовпця s ведучий елемент аks наступного жорданова перетворення. Поділивши рядок k на ведучий елемент аks, дістанемо одиницю у стовпці s і Θ у стовпці вільних членів. Отриманий рядок віднімемо від кожного іншого рядка і, помноживши на аis, від рядка цільової функції, помноживши на δs. 5) В результаті маємо симплекс – табли
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.05 с.) |

 ;
;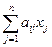 = bi (i = 1, 2, …, m1 ≤ m),
= bi (i = 1, 2, …, m1 ≤ m),  (max). Отже, будь – яку задачу лінійного програмування можна записати так:
(max). Отже, будь – яку задачу лінійного програмування можна записати так:

 ,
,  ,...,
,...,  ;
; 
 , xj ≥ 0 (j = 1, 2, …, n),
, xj ≥ 0 (j = 1, 2, …, n),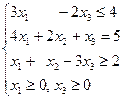



 та А4 =
та А4 =  утворюють, очевидно, лінійно незалежну систему векторів і базис векторів умов. Тому α1 є невиродженим опорним розв’язком цієї задачі, вектори А3 і А4 складають базис цього опорного розв’язку. Вектори А1 =
утворюють, очевидно, лінійно незалежну систему векторів і базис векторів умов. Тому α1 є невиродженим опорним розв’язком цієї задачі, вектори А3 і А4 складають базис цього опорного розв’язку. Вектори А1 =  , А3 =
, А3 =  ,
,  , …,
, …,  – такий базис і В =
– такий базис і В =  ∙
∙  ∙
∙ 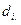 ∙
∙  ,
,  = В.
= В.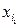 ,
,  , …,
, …,  , всі решта вільні. Матриця такого розв’язку на стовпцях основних змінних є діагональною. Отже маємо:
, всі решта вільні. Матриця такого розв’язку на стовпцях основних змінних є діагональною. Отже маємо:



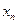
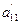
 .
.
.
.
.
.

 .
.
.
.
.
.


 .
.
.
.
.
.







 (k = 1,2,…,r). Віднімемо від останнього рядка отриманої таблиці перший рядок, помножений на
(k = 1,2,…,r). Віднімемо від останнього рядка отриманої таблиці перший рядок, помножений на 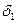




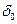
 = – f (α) (значення цільової функції на опорному розв’язку α з протилежним знаком).
= – f (α) (значення цільової функції на опорному розв’язку α з протилежним знаком). ,
, 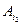 , …,
, …,  (j=1,2,…,n), δ0 =
(j=1,2,…,n), δ0 = 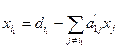 ,
,  , (k = 1,2,…,r). Підставимо ці вирази замість
, (k = 1,2,…,r). Підставимо ці вирази замість 

 ) =
) = 
 = =
= =  +
+ 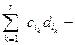
 =
=  = f (α) +
= f (α) +  =
= + f (α), δj ≤ 0. Якщо α1 = (u1, u2, …, un) – деякий інший опорний розв’язок, uj ≥ 0 (j=1,2,…,n), то f (α1) =
+ f (α), δj ≤ 0. Якщо α1 = (u1, u2, …, un) – деякий інший опорний розв’язок, uj ≥ 0 (j=1,2,…,n), то f (α1) =  + f (α) ≤ f (α), тобто розв’язок α є максимальним.
+ f (α) ≤ f (α), тобто розв’язок α є максимальним. (k = 1,2,…,r),
(k = 1,2,…,r), 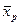 = θ, всі інші вільні змінні
= θ, всі інші вільні змінні  = 0. Такий набір значень змінних задовольняє системі обмежень: у кожному рядку k симплекс – таблиці, приведеної до базису опорного розв’язку α, маємо
= 0. Такий набір значень змінних задовольняє системі обмежень: у кожному рядку k симплекс – таблиці, приведеної до базису опорного розв’язку α, маємо  = =
= =  +
+  = (
= ( ) +
) +  =
=  + f (α) = δpθ + f (α) > f (α). Це означає, що не вироджений опорний розв’язок не є максимальним, якщо існує оцінка δp > 0 його базису. Отже, невироджений опорний розв’язок є оптимальним тоді і тільки тоді, коли всі оцінки його базису недодатні. Але будь – який опорний розв’язок можна як завгодно точно наблизити невиродженим. Оцінки базисів деякої послідовності таких наближень збігаються до оцінок деякого базису даного розв’язка і отже всі оцінки довільного оптимального опорного розв’язку недодатні.
+ f (α) = δpθ + f (α) > f (α). Це означає, що не вироджений опорний розв’язок не є максимальним, якщо існує оцінка δp > 0 його базису. Отже, невироджений опорний розв’язок є оптимальним тоді і тільки тоді, коли всі оцінки його базису недодатні. Але будь – який опорний розв’язок можна як завгодно точно наблизити невиродженим. Оцінки базисів деякої послідовності таких наближень збігаються до оцінок деякого базису даного розв’язка і отже всі оцінки довільного оптимального опорного розв’язку недодатні. (k = 1,2,…,r),
(k = 1,2,…,r),  = θ, всі інші вільні змінні
= θ, всі інші вільні змінні 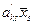 = (
= (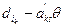 ) +
) +  =
=  ≤ 0, то й
≤ 0, то й  .
.
 .
. .
. .
. ;
; ; Θ
; Θ  (4)
(4)


