
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило побудови двоїстої задачіСодержание книги
Поиск на нашем сайте Для побудови двоїстої задачі необхідно звести пряму задачу до стандартного виду. Вважають, що задача лінійного програмування подана у стандартному вигляді, якщо для відшукання максимального значення цільової функції всі нерівності її системи обмежень приведені до виду « Якщо пряма задача лінійного програмування подана у стандартному вигляді, то двоїста задача утворюється за такими правилами: 1. Кожному обмеженню прямої задачі відповідає змінна двоїстої задачі. Кількість невідомих двоїстої задачі дорівнює кількості обмежень прямої задачі. 2. Кожній змінній прямої задачі відповідає обмеження двоїстої задачі, причому кількість обмежень двоїстої задачі дорівнює кількості невідомих прямої задачі. 3. Якщо цільова функція прямої задачі задається на пошук найбільшого значення, то цільова функція двоїстої задачі – на визначення найменшого значення, і навпаки. 4. Коефіцієнтами при змінних цільової функції двоїстої задачі є вільні члени системи обмежень прямої задачі. 5. Правими частинами системи обмежень двоїстої задачі є коефіцієнти при змінних у цільовій функції прямої задачі. 6. Матриця Пари задач лінійного програмування симетричні та несиметричні. У симетричних задачах обмеження прямої та двоїстої задач є лише нерівностями, а змінні обох задач можуть набувати лише невід’ємних значень. У несиметричних задачах деякі обмеження прямої задачі можуть бути рівняннями, а двоїстої – лише нерівностями. У цьому разі відповідні рівнянням змінні двоїстої задачі можуть набувати будь-яких значень, не обмежених знаком. Задача 6.1.1. До заданої задачі лінійного програмування записати двоїсту.
Розв’язання. Пряму задачу зведемо до стандартного вигляду. Оскільки цільова функція F мінімізується і в системі обмежень є нерівності, то вони мають бути виду «
Двоїста задача:
Оскільки перше обмеження початкової задачі є рівнянням, то відповідна йому змінна двоїстої задачі Основні теореми двоїстості Зв’язок між оптимальними розв’язками прямої та двоїстої задач встановлюють леми та теореми двоїстості (наведемо їх без доведень). Розглянемо задачі (6.1)-(6.3) та (6.4)-(6.6) з економічною інтерпретацією. Лема 6.2.1(основна нерівність теорії двоїстості). Якщо
Лема 6.2.2(достатня умова оптимальності). Якщо Теорема (перша теорема двоїстості). Якщо одна з пари спряжених задач має оптимальний план, то й друга задача також має розв’язок, причому для оптимальних розв’язків значення цільових функцій обох задач збігаються, тобто Якщо цільова функція однієї із задач необмежена, то спряжена задача також не має розв’язку. Слід зауважити, що коли одна із задач не має допустимого розв’язку, то двоїста до неї задача також може не мати допустимого розв’язку, тобто зворотне твердження щодо другої частини теореми в загальному випадку не виконується. Економічний зміст першої теореми двоїстості. Максимальний прибуток ( Теорема (друга теорема двоїстості для симетричних задач). Для того, щоб плани
Економічний зміст другої теореми двоїстості стосовно оптимальногоплану Якщо ж витрати ресурсу дорівнюють його наявному обсягові Економічне тлумачення другої теореми двоїстості щодо оптимальногоплану Якщо витрати на виробництво Існування двоїстих змінних уможливлює зіставлення витрат на виробництво і цін на продукцію, на підставі чого обґрунтовується висновок про доцільність чи недоцільність виробництва кожного виду продукції. Крім цього, значення двоїстої оцінки характеризує зміну значення цільової функції, що зумовлена малими змінами вільного члена відповідного обмеження. Дане твердження формулюється у вигляді такої теореми. Теорема (третя теорема двоїстості). Компоненти оптимального плану двоїстої задачі
Економічний зміст третьої теореми двоїстості. Двоїсті оцінки є унікальним інструментом, який дає змогу зіставляти непорівнянні речі Очевидно, що неможливим є просте зіставлення величин, які мають різні одиниці вимірювання. Якщо взяти як приклад виробничу задачу, то цікавим є питання: як змінюватиметься значення цільової функції (може вимірюватися в грошових одиницях) за зміни обсягів різних ресурсів (можуть вимірюватися в тоннах, люд./год, га тощо). Використовуючи третю теорему двоїстості, можна легко визначити вплив на зміну значення цільової функції збільшення чи зменшення обсягів окремих ресурсів: числові значення двоїстих оцінок показують, на яку величину змінюється цільова функція за зміни обсягу відповідного даній оцінці ресурсу Кожну з двох спряжених задач можна розв’язати окремо, проте встановлені теоремами двоїстості залежності між оптимальними планами прямої та двоїстої задач уможливлюють знаходження розв’язку двоїстої задачі за наявності оптимального плану, і навпаки. Задача 6.2.1. До заданої задачі лінійного програмування записати двоїсту задачу. Розв’язавши двоїсту задачу графічно, визначити оптимальний план прямої задачі.
Розв’язання. За відповідними правилами побудуємо двоїсту задачу:
Зауважимо, що задачі несиметричні, і тому змінна Двоїста задача має дві змінні, а отже, її можна розв’язати графічно (мал. 6.2.1).
Мал. 6.2.1. Найбільшого значення цільова функція двоїстої задачі F досягає в точці В багатокутника ABCD. Її координати визначимо розв’язанням системи рівнянь:
Отже, Оптимальний план прямої задачі визначимо за допомогою співвідношень другої теореми двоїстості. Підставимо
Оскільки перше обмеження для оптимального плану двоїстої задачі виконується як строга нерівність, то перша змінна прямої задачі дорівнюватиме нулю Тепер проаналізуємо оптимальний план двоїстої задачі. Оскільки друга компонента плану Об’єднуючи здобуту інформацію, можна записати систему обмежень прямої задачі як систему двох рівнянь, в якій
тобто Умова Розглянемо економічну інтерпретацію двоїстих задач та двоїстих оцінок на прикладі. Задача 6.2.2. Для виготовлення трьох видів виробів А, В, С використовують три різні види сировини. Кожен з видів сировини може бути використаний в кількості, не більшій 180, 210 та 244 кг відповідно. Норми витрат кожного з видів сировини на одиницю продукції даного виду та ціна одиниці продукції кожного з видів наведені в таблиці 6.2.1. Визначити план випуску продукції, при якому її вартість буде максимальною та оцінити кожен з видів сировини. Оцінки кожного з видів сировини повинні бути такі, щоб оцінка всієї сировини була мінімальною, а сумарна оцінка сировини, на одиницю продукції кожного виду – не менша за ціну одиниці продукції даного виду. Таблиця 6.2.1.
Розв’язання. Нехай виготовляють х1 виробів А, х2 виробів В та х3 виробів С. Для визначення оптимального плану виробництва потрібно розв’язати задачу на максимізацію цільової функції F=10 х1+14 х2+12 х3, при таких умовах: Припишемо до кожного з видів сировини двоїсту оцінку, яка відповідно дорівнює За умовою задачі, Отримали симетричну пару двоїстих задач. Розв’язання прямої задачі дає оптимальний план виготовлення виробів А, В, С, а розв’язання двоїстої – оптимальну систему оцінок сировини, яка використовується для виготовлення цих виробів. Щоб розв’язати ці задачі, необхідно спочатку знайти розв’язок однієї з них. Розв’яжемо пряму задачу (її система обмежень містить лише нерівності виду « Таблиця 6.2.2.
З даної таблиці видно, що оптимальним планом виготовлення виробів є такий план, при якому виготовляються 82 виробів В та 16 виробів С. В цьому випадку залишається не використаним 80 кг сировини ІІ виду, а загальна вартість виробів дорівнює 1340 ум.од. З таблиці 6.2.2 також видно, що оптимальний розв’язок двоїстої задачі має вигляд: Змінні Таким чином, додатну двоїсту оцінку мають лише ті види сировини, які повністю використовуються при оптимальному плані виробництва продукції. Тому двоїсті оцінки визначають дефіцитність сировини що використовує підприємство. Більш того, величина даної двоїстої оцінки показує, на скільки зростає максимальне значення цільової функції прямої задачі при збільшенні кількості сировини відповідного виду на 1 кг. Так, збільшення кількості сировини І виду на 1 кг призведе до появи можливості знайти новий оптимальний план виготовлення виробів, при якому загальна вартість виготовленої продукції зросте на 5,75 ум.од. і становитиме 1340+5,75=1345,75 ум.од. При цьому числа, що стоять в стовпці вектора Р4 (табл. 6.2.2), показують, що таке збільшення загальної вартості виготовленої продукції може бути досягнуто за рахунок збільшення випуску виробів В на Обчислюючи мінімальне значення цільової функції двоїстої задачі При підстановці оптимальних двоїстих оцінок в систему обмежень двоїстої задачі матимемо: Перше обмеження двоїстої задачі виконується як строга нерівність. Це означає, що двоїста оцінка сировини, що йде на виготовлення одного виробу виду А, вища ціни цього виробу, отже, випускати ці вироби невигідно. Його виготовлення й непередбачено оптимальним планом прямої задачі. Друге й третє обмеження двоїстої задачі виконуються як строгі рівності. Це означає, що двоїста оцінка сировини, що використовується для виготовлення одиниці виробів В і С відповідно, дорівнюють їх цінам. Тому випускати ці два види продукції по двоїстим оцінкам економічно вигідно. Їх виготовлення й передбачено оптимальним планом прямої задачі. Таким чином, двоїсті оцінки пов’язані з оптимальним планом прямої задачі. Будь-яка зміна вихідних данних прямої задачі може вплинути як на її оптимальний план, так і на систему оптимальних двоїстих оцінок.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 616; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 », а для задачі для відшукання мінімального значення – «
», а для задачі для відшукання мінімального значення – « ».
». , що складається з коефіцієнтів при змінних у системі обмежень прямої задачі, і матриця коефіцієнтів у системі обмежень двоїстої задачі
, що складається з коефіцієнтів при змінних у системі обмежень прямої задачі, і матриця коефіцієнтів у системі обмежень двоїстої задачі  утворюються одна з одної транспонуванням, тобто заміною рядків стовпчиками, а стовпчиків – рядками.
утворюються одна з одної транспонуванням, тобто заміною рядків стовпчиками, а стовпчиків – рядками.



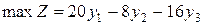 ,
,

 може набувати як додатного, так і від’ємного значення.
може набувати як додатного, так і від’ємного значення. та
та  - допустимі розв’язки відповідно прямої та двоїстої задач, то виконується нерівність
- допустимі розв’язки відповідно прямої та двоїстої задач, то виконується нерівність або
або  .
. та
та  - допустимі розв’язки відповідно прямої та двоїстої задач, для яких виконується рівність
- допустимі розв’язки відповідно прямої та двоїстої задач, для яких виконується рівність  , то
, то  - оптимальні розв’язки відповідних задач.
- оптимальні розв’язки відповідних задач.
 ) підприємство отримує за умови виробництва продукції згідно з оптимальним планом
) підприємство отримує за умови виробництва продукції згідно з оптимальним планом  воно може мати, реалізувавши ресурси за оптимальними цінами
воно може мати, реалізувавши ресурси за оптимальними цінами  на підставі основної нерівності теорії двоїстості можна стверджувати, що прибутки від реалізації продукції завжди менші, ніж витрати на її виробництво.
на підставі основної нерівності теорії двоїстості можна стверджувати, що прибутки від реалізації продукції завжди менші, ніж витрати на її виробництво. та
та  відповідних спряжених задач були оптимальними, необхідно і достатньо, щоб виконувалися умови доповнюючої нежорсткості:
відповідних спряжених задач були оптимальними, необхідно і достатньо, щоб виконувалися умови доповнюючої нежорсткості:
 , то відповідна оцінка такого ресурсу
, то відповідна оцінка такого ресурсу  (компонента оптимального плану двоїстої задачі) буде дорівнювати нулю, тобто такий ресурс за даних умов для виробництва не є «цінним».
(компонента оптимального плану двоїстої задачі) буде дорівнювати нулю, тобто такий ресурс за даних умов для виробництва не є «цінним». -те обмеження виконується як нерівність, тобто всі витрати на виробництво одиниці
-те обмеження виконується як нерівність, тобто всі витрати на виробництво одиниці  , виробництво такого виду продукції є недоцільним, і в оптимальному плані прямої задачі обсяг такої продукції
, виробництво такого виду продукції є недоцільним, і в оптимальному плані прямої задачі обсяг такої продукції 
 дорівнює нулю.
дорівнює нулю.
 дорівнюють значенням частинних похідних від цільової функції
дорівнюють значенням частинних похідних від цільової функції  за відповідними аргументами
за відповідними аргументами  або
або
 .
.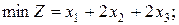



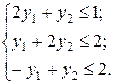

 - лише невід’ємна.
- лише невід’ємна.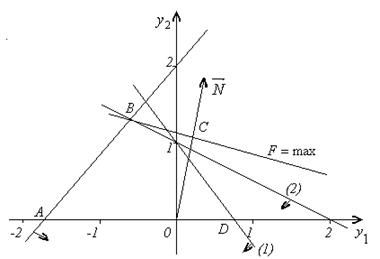


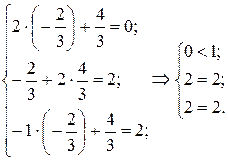
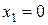 (перша частина теореми двоїстості).
(перша частина теореми двоїстості). додатна, то друге обмеження прямої задачі для
додатна, то друге обмеження прямої задачі для 

 виконується, і тому
виконується, і тому  є оптимальними планами відповідно прямої та двоїстої задачі.
є оптимальними планами відповідно прямої та двоїстої задачі.
 . Тоді загальна оцінка сировини, яка йде на виготовлення продукції, становитиме:
. Тоді загальна оцінка сировини, яка йде на виготовлення продукції, становитиме:  .
.














 та
та  є умовними двоїстими оцінками сировини, І та ІІІ видів відповідно. Ці оцінки відмінні від нуля, а сировина І та ІІІ видів повністю використовується при оптимальному плані виготовлення продукції. Двоїста оцінка одиниці сировини ІІ виду дорівнює нулю. Цей вид сировини не повністю використовується при оптимальному плані виробництва продукції.
є умовними двоїстими оцінками сировини, І та ІІІ видів відповідно. Ці оцінки відмінні від нуля, а сировина І та ІІІ видів повністю використовується при оптимальному плані виготовлення продукції. Двоїста оцінка одиниці сировини ІІ виду дорівнює нулю. Цей вид сировини не повністю використовується при оптимальному плані виробництва продукції. од. та скорочення випуску виробів С на
од. та скорочення випуску виробів С на  кг. Аналогічно, збільшення на 1 кг сировини ІІІ виду дозволить знайти новий оптимальний план виготовлення виробів, при якому загальна вартість виготовленої продукції зросте на 1,25 ум.од. й становитиме 1340+1,25=1341,25 ум.од. Це буде досягнуто внаслідок збільшення випуску виробів С на
кг. Аналогічно, збільшення на 1 кг сировини ІІІ виду дозволить знайти новий оптимальний план виготовлення виробів, при якому загальна вартість виготовленої продукції зросте на 1,25 ум.од. й становитиме 1340+1,25=1341,25 ум.од. Це буде досягнуто внаслідок збільшення випуску виробів С на  , бачимо, що воно співпадає з максимальним значенням цільової функції вихідної задачі.
, бачимо, що воно співпадає з максимальним значенням цільової функції вихідної задачі.



