
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Історія зародження і створення лінійного програмуванняСодержание книги
Поиск на нашем сайте
Основні поняття систем лінійних рівнянь і нерівностей Розглянемо спочатку узагальнення деяких понять в просторі Вираз виду
називають лінійним рівнянням з Вираз виду
де Систему рівнянь виду (2.1) називають системою лінійних рівнянь (СЛР):
Систему нерівностей виду (2.2) називають системою лінійнихнерівностей (СЛН):
Систему рівнянь (2.3) можна представити у векторній формі:
де та у матричній формі:
Аналогічно можна представити і СЛН (2.4). Якщо Під базисом розуміють максимально лінійно незалежну систему векторів простору Вектор СЛР (2.3) сумісна, якщо вона має хоча б один розв’язок, у противному випадку СЛР – несумісна. СЛР (2.3) визначена, якщо вона має лише один розв’язок, у противному випадку СЛР – невизначена. Під розв’язком СЛР розуміють вектор Аналогічно вводять поняття сумісності і визначеності СЛН. Множина всіх точок Множина всіх точок Якщо Підмножина простору Комбінація векторів Якщо М є деякою множиною векторів з
Задача 6.1.1. До заданої задачі лінійного програмування записати двоїсту.
Розв’язання. Пряму задачу зведемо до стандартного вигляду. Оскільки цільова функція F мінімізується і в системі обмежень є нерівності, то вони мають бути виду «
Двоїста задача:
Оскільки перше обмеження початкової задачі є рівнянням, то відповідна йому змінна двоїстої задачі Основні теореми двоїстості Зв’язок між оптимальними розв’язками прямої та двоїстої задач встановлюють леми та теореми двоїстості (наведемо їх без доведень). Розглянемо задачі (6.1)-(6.3) та (6.4)-(6.6) з економічною інтерпретацією. Лема 6.2.1(основна нерівність теорії двоїстості). Якщо
Лема 6.2.2(достатня умова оптимальності). Якщо Теорема (перша теорема двоїстості). Якщо одна з пари спряжених задач має оптимальний план, то й друга задача також має розв’язок, причому для оптимальних розв’язків значення цільових функцій обох задач збігаються, тобто Якщо цільова функція однієї із задач необмежена, то спряжена задача також не має розв’язку. Слід зауважити, що коли одна із задач не має допустимого розв’язку, то двоїста до неї задача також може не мати допустимого розв’язку, тобто зворотне твердження щодо другої частини теореми в загальному випадку не виконується. Економічний зміст першої теореми двоїстості. Максимальний прибуток ( Теорема (друга теорема двоїстості для симетричних задач). Для того, щоб плани
Економічний зміст другої теореми двоїстості стосовно оптимальногоплану Якщо ж витрати ресурсу дорівнюють його наявному обсягові Економічне тлумачення другої теореми двоїстості щодо оптимальногоплану Якщо витрати на виробництво Існування двоїстих змінних уможливлює зіставлення витрат на виробництво і цін на продукцію, на підставі чого обґрунтовується висновок про доцільність чи недоцільність виробництва кожного виду продукції. Крім цього, значення двоїстої оцінки характеризує зміну значення цільової функції, що зумовлена малими змінами вільного члена відповідного обмеження. Дане твердження формулюється у вигляді такої теореми. Теорема (третя теорема двоїстості). Компоненти оптимального плану двоїстої задачі
Економічний зміст третьої теореми двоїстості. Двоїсті оцінки є унікальним інструментом, який дає змогу зіставляти непорівнянні речі Очевидно, що неможливим є просте зіставлення величин, які мають різні одиниці вимірювання. Якщо взяти як приклад виробничу задачу, то цікавим є питання: як змінюватиметься значення цільової функції (може вимірюватися в грошових одиницях) за зміни обсягів різних ресурсів (можуть вимірюватися в тоннах, люд./год, га тощо). Використовуючи третю теорему двоїстості, можна легко визначити вплив на зміну значення цільової функції збільшення чи зменшення обсягів окремих ресурсів: числові значення двоїстих оцінок показують, на яку величину змінюється цільова функція за зміни обсягу відповідного даній оцінці ресурсу Кожну з двох спряжених задач можна розв’язати окремо, проте встановлені теоремами двоїстості залежності між оптимальними планами прямої та двоїстої задач уможливлюють знаходження розв’язку двоїстої задачі за наявності оптимального плану, і навпаки. Задача 6.2.1. До заданої задачі лінійного програмування записати двоїсту задачу. Розв’язавши двоїсту задачу графічно, визначити оптимальний план прямої задачі.
Розв’язання. За відповідними правилами побудуємо двоїсту задачу:
Зауважимо, що задачі несиметричні, і тому змінна Двоїста задача має дві змінні, а отже, її можна розв’язати графічно (мал. 6.2.1).
Мал. 6.2.1. Найбільшого значення цільова функція двоїстої задачі F досягає в точці В багатокутника ABCD. Її координати визначимо розв’язанням системи рівнянь:
Отже, Оптимальний план прямої задачі визначимо за допомогою співвідношень другої теореми двоїстості. Підставимо
Оскільки перше обмеження для оптимального плану двоїстої задачі виконується як строга нерівність, то перша змінна прямої задачі дорівнюватиме нулю Тепер проаналізуємо оптимальний план двоїстої задачі. Оскільки друга компонента плану Об’єднуючи здобуту інформацію, можна записати систему обмежень прямої задачі як систему двох рівнянь, в якій
тобто Умова Розглянемо економічну інтерпретацію двоїстих задач та двоїстих оцінок на прикладі. Задача 6.2.2. Для виготовлення трьох видів виробів А, В, С використовують три різні види сировини. Кожен з видів сировини може бути використаний в кількості, не більшій 180, 210 та 244 кг відповідно. Норми витрат кожного з видів сировини на одиницю продукції даного виду та ціна одиниці продукції кожного з видів наведені в таблиці 6.2.1. Визначити план випуску продукції, при якому її вартість буде максимальною та оцінити кожен з видів сировини. Оцінки кожного з видів сировини повинні бути такі, щоб оцінка всієї сировини була мінімальною, а сумарна оцінка сировини, на одиницю продукції кожного виду – не менша за ціну одиниці продукції даного виду. Таблиця 6.2.1.
Розв’язання. Нехай виготовляють х1 виробів А, х2 виробів В та х3 виробів С. Для визначення оптимального плану виробництва потрібно розв’язати задачу на максимізацію цільової функції F=10 х1+14 х2+12 х3, при таких умовах: Припишемо до кожного з видів сировини двоїсту оцінку, яка відповідно дорівнює За умовою задачі, Отримали симетричну пару двоїстих задач. Розв’язання прямої задачі дає оптимальний план виготовлення виробів А, В, С, а розв’язання двоїстої – оптимальну систему оцінок сировини, яка використовується для виготовлення цих виробів. Щоб розв’язати ці задачі, необхідно спочатку знайти розв’язок однієї з них. Розв’яжемо пряму задачу (її система обмежень містить лише нерівності виду « Таблиця 6.2.2.
З даної таблиці видно, що оптимальним планом виготовлення виробів є такий план, при якому виготовляються 82 виробів В та 16 виробів С. В цьому випадку залишається не використаним 80 кг сировини ІІ виду, а загальна вартість виробів дорівнює 1340 ум.од. З таблиці 6.2.2 також видно, що оптимальний розв’язок двоїстої задачі має вигляд: Змінні Таким чином, додатну двоїсту оцінку мають лише ті види сировини, які повністю використовуються при оптимальному плані виробництва продукції. Тому двоїсті оцінки визначають дефіцитність сировини що використовує підприємство. Більш того, величина даної двоїстої оцінки показує, на скільки зростає максимальне значення цільової функції прямої задачі при збільшенні кількості сировини відповідного виду на 1 кг. Так, збільшення кількості сировини І виду на 1 кг призведе до появи можливості знайти новий оптимальний план виготовлення виробів, при якому загальна вартість виготовленої продукції зросте на 5,75 ум.од. і становитиме 1340+5,75=1345,75 ум.од. При цьому числа, що стоять в стовпці вектора Р4 (табл. 6.2.2), показують, що таке збільшення загальної вартості виготовленої продукції може бути досягнуто за рахунок збільшення випуску виробів В на Обчислюючи мінімальне значення цільової функції двоїстої задачі При підстановці оптимальних двоїстих оцінок в систему обмежень двоїстої задачі матимемо: Перше обмеження двоїстої задачі виконується як строга нерівність. Це означає, що двоїста оцінка сировини, що йде на виготовлення одного виробу виду А, вища ціни цього виробу, отже, випускати ці вироби невигідно. Його виготовлення й непередбачено оптимальним планом прямої задачі. Друге й третє обмеження двоїстої задачі виконуються як строгі рівності. Це означає, що двоїста оцінка сировини, що використовується для виготовлення одиниці виробів В і С відповідно, дорівнюють їх цінам. Тому випускати ці два види продукції по двоїстим оцінкам економічно вигідно. Їх виготовлення й передбачено оптимальним планом прямої задачі. Таким чином, двоїсті оцінки пов’язані з оптимальним планом прямої задачі. Будь-яка зміна вихідних данних прямої задачі може вплинути як на її оптимальний план, так і на систему оптимальних двоїстих оцінок. Історія зародження і створення лінійного програмування
Кожна людина щодня, не завжди усвідомлюючи це, вирішує проблему: як одержати найбільший ефект, володіючи обмеженими засобами. Наші засоби і ресурси завжди обмежені. Життя було б менш цікаве, якби це було не так. Не важко виграти бій, маючи армію в 10 разів більшу, ніж у супротивника. Щоб досягти найбільшого ефекту, маючи обмежені засоби, треба скласти план чи програму дій. Раніше план в таких випадках складався «на око». У середині XX століття був створений спеціальний математичний апарат, що допомагає це робити «по науці». Відповідний розділ математики називається математичним програмуванням. Слово «програмування» тут і в аналогічних термінах («лінійне програмування», «динамічне програмування» і т.п.) зобов'язане почасти історичному непорозумінню, почасти неточному перекладу з англійської мови: mathematical programming, що означає розроблення на основі математичних розрахунків програми дій для досягнення обраної мети. З програмуванням для ЕОМ математичне програмування має лише те спільне, що більшість виникаючих на практиці задач математичного програмування занадто громіздкі для ручного розрахунку, тому розв’язати їх можна тільки за допомогою ЕОМ, попередньо склавши програму. В суто математичному плані деякі оптимізаційні задачі були відомі ще в стародавній Греції. Однак, сучасне математичне програмування передусім розглядає властивості та розв'язки математичних моделей економічних процесів. Тому початком його розвитку як самостійного наукового напрямку слід вважати перші спроби застосування методів математичного програмування в прикладних дослідженнях, насамперед в економіці. Справжнім початком математичного програмування в сучасному розумінні вважають 1939р., коли була надрукована брошура Леоніда Віталійовича Канторовича «Математичні методи організації і планування виробництва». Наприкінці 30-х років в Ленінградському університеті ним уперше були сформульовані та досліджувались основні задачі, критерії оптимальності, економічна інтерпретація, методи розв'язання та геометрична інтерпретація результатів розв'язання задач лінійного програмування. Але, оскільки методи, викладені Л.В.Канторовичем, були мало придатні для ручного рахунку, а швидкодіючих обчислювальних машин у той час не існувало, то роботи Л.В.Канторовича залишилася майже не поміченими. В автобіографії, представленої в Нобелівський комітет, Леонід Віталійович Канторович розповідає про події, що трапилися в 1939 році. До нього, 26-літнього професора-математика, звернулися за консультацією співробітники лабораторії планерного тресту, яким потрібно було вирішити задачу про найбільш вигідний розподіл матеріалу між верстатами. Ця задача зводилася до відшукання максимуму лінійної функції, заданої на багатограннику. Максимум такої функції досягався у вершині, однак число вершин у цій задачі досягало мільярду. Тому простий перебір вершин не підходив. Леонід Віталійович писав: «Виявилось, що ця задача не є випадковою. Я знайшов велике число різноманітних по змісту задач, що мають аналогічний математичний характер: найкраще використання посівних площ, вибір завантаження устаткування, раціональний розкрій матеріалу, розподіл транспортних вантажопотоків... Це наполегливо спонукало мене до пошуку ефективного методу їхнього розв’язання». І вже влітку 1939 року була здана в набір книга Л.В.Канторовича «Математичні методи організації і планування виробництва», в якій закладалися основи того, що нині називається математичною економікою. Однак ідеї Л.В.Канторовича не зустріли розуміння в момент їхнього зародження і його робота була перервана. Концепції Леоніда Віталійовича незабаром після війни були перевідкриті на заході. Американський економіст Т.Купманс протягом багатьох років привертав увагу математиків до ряду задач, пов'язаних з військовою тематикою. Він активно сприяв тому, щоб був організований математичний колектив для розробки цих проблем. У підсумку було усвідомлено, що треба навчитися розв’язувати задачі про знаходження экстремумів лінійних функцій на багатогранниках, що задаються лінійними нерівностями. За пропозицією Купманса цей розділ математики одержав назву лінійного програмування. 1947 року Дж.Данцигом також був розроблений основний метод розв'язування задач лінійного програмування — симплексний метод, що вважається початком формування лінійного програмування як самостійного напрямку в математичному програмуванні. Ідеї лінійного програмування протягом п'яти шести років одержали грандіозне поширення в світі, й імена Купманса і Данцига стали всюди широко відомі. Наступним кроком стали праці Дж.Неймана (1947 р.) щодо розвитку концепції двоїстості, що уможливило розширення практичної сфери застосування методів лінійного програмування. Приблизно в цей час Купманс довідався, що ще до війни в далекій Росії вже було зроблено щось схоже на розробку основ лінійного програмування. Як легко було б Данцигові і Купмансу проігнорувати цю інформацію! Маленька книжечка, видана незначним тиражем, звернена навіть не до економістів, а до організаторів виробництва, з мінімумом математики, без чітко описаних алгоритмів, без доведень теорем – словом, чи варто брати таку книжку до уваги. Але Купманс наполягає на перекладі і виданні на заході книги Канторовича. Його ім'я й ідеї стають відомі всім. У своїй монографії Дж.Данциг зазначає, що Л.В.Канторовича слід визнати першим, хто виявив, що широке коло важливих виробничих задач може бути подане у чіткому математичному формулюванні, яке уможливлює підхід до таких задач з кількісного боку та розв'язання їх чисельними методами. Л.В.Канторович продовжує писати математичні роботи, навіяні економічними ідеями, бере участь і в конкретних розробках на виробництві. При цьому (одночасно з Данцигом, але, не знаючи його робіт) він розробляє метод, пізніше названий симплексним методом. Як тільки в 50-і роки утвориться маленький просвіт, і дещо з забороненого стає можливим, він організовує групу студентів на економічному факультеті Ленінградського університету для навчання методам оптимального планування. А починаючи з 1960 року, Леонід Віталійович займається тільки економікою і позв'язаними з нею математичними проблемами. Його внесок в цій області був відзначений Ленінською премією в 1965 році, а згодом, разом з Купмасом, Л.В.Канторович одержує Нобелівську премію в 1975 році за «внесок у розробку теорії й оптимального використання ресурсів в економіці». Періодом найінтенсивнішого розвитку математичного програмування є п'ятдесяті роки. У цей час з'являються розробки нових алгоритмів, теоретичні дослідження з різних напрямків математичного програмування: 1951 року — праця Г.Куна і А.Таккера, в якій наведено необхідні та достатні умови оптимальності нелінійних задач; 1954 року — Чарнес і Лемке розглянули наближений метод розв'язання задач з сепарабельним опуклим функціоналом та лінійними обмеженнями; 1955 року — ряд робіт, присвячених квадратичному програмуванню. У п'ятдесятих роках сформувався новий напрямок математичного програмування — динамічне програмування, значний вклад у розвиток якого вніс американський математик Р.Белман. На жаль, у період найбурхливішого розвитку математичного програмування за кордоном у Радянському Союзі не спостерігалося значних досягнень через штучні ідеологічні обмеження. Відродження досліджень з математичного моделювання економіки почалося в 60-80-тих роках і стосувалося опису «системи оптимального функціонування соціалістичної економіки». Серед радянських вчених того періоду слід виокремити праці В.С.Немчинова, В.В.Новожилова, Н.П.Федоренка, С.С.Шаталіна, В.М.Глушкова, В.С.Михалевича, Ю.М.Єрмольєва та ін. Математичною основою лінійного програмування є лінійна алгебра, точніше – деяка її частина. Можна сказати, що лінійне програмування дещо омолодило лінійну алгебру, воно визначило цікаві нові шляхи виходу її в практику і привернуло увагу до певних її розділів та теоретичних задач (наприклад, теорії систем лінійних нерівностей), які до цього значною мірою залишалися поза увагою математиків.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

 довільної скінченної розмірності
довільної скінченної розмірності  над полем дійсних чисел (
над полем дійсних чисел ( ).
). (2.1)
(2.1) (2.2)
(2.2) - це один із знаків
- це один із знаків  , називають лінійною нерівністю.
, називають лінійною нерівністю. (2.3)
(2.3) (2.4)
(2.4) ,
, ,
,  ,…,
,…,  ,
, 
 , де
, де  ,
,  ,
, 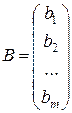 .
. , то матимем відповідно однорідну систему лінійних рівнянь або нерівностей.
, то матимем відповідно однорідну систему лінійних рівнянь або нерівностей. називають лінійною комбінацією векторів
називають лінійною комбінацією векторів  , якщо
, якщо  .
. , який перетворює всі рівності системи в правильні числові рівності.
, який перетворює всі рівності системи в правильні числові рівності. і
і  , то множина М всіх векторів виду
, то множина М всіх векторів виду  при
при  називається
називається  і
і  . Обмеження
. Обмеження  є опуклою, якщо всі
є опуклою, якщо всі  і
і  .
.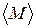 ,
, 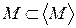 . Множину
. Множину 


 ». Тому друге обмеження задачі необхідно помножити на (-1). При цьому знак нерівності зміниться на протилежний. Отримаємо:
». Тому друге обмеження задачі необхідно помножити на (-1). При цьому знак нерівності зміниться на протилежний. Отримаємо:
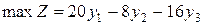 ,
,

 може набувати як додатного, так і від’ємного значення.
може набувати як додатного, так і від’ємного значення. та
та  - допустимі розв’язки відповідно прямої та двоїстої задач, то виконується нерівність
- допустимі розв’язки відповідно прямої та двоїстої задач, то виконується нерівність або
або  .
. та
та  - допустимі розв’язки відповідно прямої та двоїстої задач, для яких виконується рівність
- допустимі розв’язки відповідно прямої та двоїстої задач, для яких виконується рівність  , то
, то  - оптимальні розв’язки відповідних задач.
- оптимальні розв’язки відповідних задач.
 ) підприємство отримує за умови виробництва продукції згідно з оптимальним планом
) підприємство отримує за умови виробництва продукції згідно з оптимальним планом  воно може мати, реалізувавши ресурси за оптимальними цінами
воно може мати, реалізувавши ресурси за оптимальними цінами  на підставі основної нерівності теорії двоїстості можна стверджувати, що прибутки від реалізації продукції завжди менші, ніж витрати на її виробництво.
на підставі основної нерівності теорії двоїстості можна стверджувати, що прибутки від реалізації продукції завжди менші, ніж витрати на її виробництво. та
та  відповідних спряжених задач були оптимальними, необхідно і достатньо, щоб виконувалися умови доповнюючої нежорсткості:
відповідних спряжених задач були оптимальними, необхідно і достатньо, щоб виконувалися умови доповнюючої нежорсткості:
 , то відповідна оцінка такого ресурсу
, то відповідна оцінка такого ресурсу  (компонента оптимального плану двоїстої задачі) буде дорівнювати нулю, тобто такий ресурс за даних умов для виробництва не є «цінним».
(компонента оптимального плану двоїстої задачі) буде дорівнювати нулю, тобто такий ресурс за даних умов для виробництва не є «цінним». -те обмеження виконується як нерівність, тобто всі витрати на виробництво одиниці
-те обмеження виконується як нерівність, тобто всі витрати на виробництво одиниці  , виробництво такого виду продукції є недоцільним, і в оптимальному плані прямої задачі обсяг такої продукції
, виробництво такого виду продукції є недоцільним, і в оптимальному плані прямої задачі обсяг такої продукції 
 дорівнює нулю.
дорівнює нулю.
 дорівнюють значенням частинних похідних від цільової функції
дорівнюють значенням частинних похідних від цільової функції  за відповідними аргументами
за відповідними аргументами  або
або
 .
.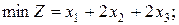



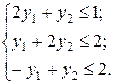

 - лише невід’ємна.
- лише невід’ємна.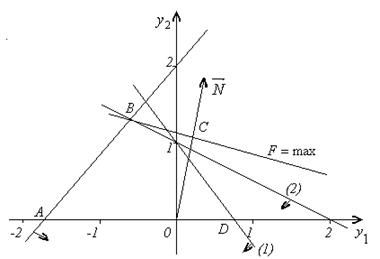


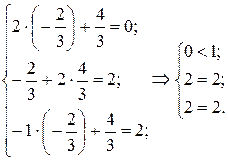
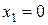 (перша частина теореми двоїстості).
(перша частина теореми двоїстості). додатна, то друге обмеження прямої задачі для
додатна, то друге обмеження прямої задачі для 

 виконується, і тому
виконується, і тому  є оптимальними планами відповідно прямої та двоїстої задачі.
є оптимальними планами відповідно прямої та двоїстої задачі.
 . Тоді загальна оцінка сировини, яка йде на виготовлення продукції, становитиме:
. Тоді загальна оцінка сировини, яка йде на виготовлення продукції, становитиме:  .
.

 »). Її розв’язання наведено в таблиці 6.2.2.
»). Її розв’язання наведено в таблиці 6.2.2.












 та
та  є умовними двоїстими оцінками сировини, І та ІІІ видів відповідно. Ці оцінки відмінні від нуля, а сировина І та ІІІ видів повністю використовується при оптимальному плані виготовлення продукції. Двоїста оцінка одиниці сировини ІІ виду дорівнює нулю. Цей вид сировини не повністю використовується при оптимальному плані виробництва продукції.
є умовними двоїстими оцінками сировини, І та ІІІ видів відповідно. Ці оцінки відмінні від нуля, а сировина І та ІІІ видів повністю використовується при оптимальному плані виготовлення продукції. Двоїста оцінка одиниці сировини ІІ виду дорівнює нулю. Цей вид сировини не повністю використовується при оптимальному плані виробництва продукції. од. та скорочення випуску виробів С на
од. та скорочення випуску виробів С на  кг. Аналогічно, збільшення на 1 кг сировини ІІІ виду дозволить знайти новий оптимальний план виготовлення виробів, при якому загальна вартість виготовленої продукції зросте на 1,25 ум.од. й становитиме 1340+1,25=1341,25 ум.од. Це буде досягнуто внаслідок збільшення випуску виробів С на
кг. Аналогічно, збільшення на 1 кг сировини ІІІ виду дозволить знайти новий оптимальний план виготовлення виробів, при якому загальна вартість виготовленої продукції зросте на 1,25 ум.од. й становитиме 1340+1,25=1341,25 ум.од. Це буде досягнуто внаслідок збільшення випуску виробів С на  , бачимо, що воно співпадає з максимальним значенням цільової функції вихідної задачі.
, бачимо, що воно співпадає з максимальним значенням цільової функції вихідної задачі.



