
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття задачі лінійного програмування та різні форми її заданняСодержание книги
Поиск на нашем сайте Під задачею лінійного програмування в загальному вигляді розуміють задачу знаходження мінімуму (максимуму) лінійної функції від Задача 3.1. Завод додатково освоїв випуск продукції чотирьох асортиментів Таблиця 3.1.
Визначити, яку кількість треба випускати заводу кожного з видів продукції
Складемо математичну модель цієї задачі, тобто опишемо її в термінах математичної символіки. Позначимо через За змістом задачі невідомі Прибуток від реалізації випущеної продукції (позначимо її через Дані системи лінійних нерівностей і лінійна функція визначають математичну модель розглянутої задачі: знайти такі значення змінних Тепер розглянемо чисельне розв’язання таких задач. У наведеній задачі значення змінних Якщо позначити символом
і перетворюють в екстремум (максимум або мінімум) лінійну функцію
Цю функцію називають цільовою функцією, вона моделює поставлену в задачі мету. У задачах лінійного програмування можна виділити два типи однорідних обмежень на вибір змінних: у вигляді лінійних нерівностей або у вигляді лінійних рівнянь. Крім того, для спрощення можна формулювати задачу лише для мінімуму цільової функції. Якщо ж в конкретній задачі треба визначити максимум функції З цього випливають три форми задач лінійного програмування: 1) загальна задача лінійного програмування; 2) стандартна (симетрична); 3) канонічна. Загальна задача лінійного програмування подається у вигляді:
за умов:
Отже, потрібно знайти значення змінних Для загальної задачі лінійного програмування використовуються такі поняття. Вектор Допустимий план Опорний план Опорний план Стандартна (симетрична) задача лінійного програмування подається у вигляді:
Задачу (3.1)-(3.3) можна легко звести до канонічної форми, тобто до такого вигляду, коли в системі обмежень (3.2) всі Якщо якесь
то останню завжди можна звести до рівності, увівши додаткову змінну
Аналогічно обмеження виду
зводиться до рівності, віднімаючи від лівої частини додаткову змінну
Така заміна нерівностей рівняннями за допомогою введення додаткових змінних не змінить розв’язку початкової задачі. Задачі лінійного програмування можна розв’язувати графічно і аналітично.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

 змінних на множині розв’язків системи лінійних нерівностей або лінійних рівнянь. Розглянемо це на конкретному прикладі.
змінних на множині розв’язків системи лінійних нерівностей або лінійних рівнянь. Розглянемо це на конкретному прикладі. . Для випуску цієї продукції потрібна сировина чотирьох видів
. Для випуску цієї продукції потрібна сировина чотирьох видів 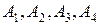 , яку завод може щомісячно виділяти в обмеженій кількості. Кількість сировини кожного виду, необхідної для виготовлення кожного виду продукції, ціна кожного виду продукції, а також лімітоване щомісячне надходження потрібної сировини подано в таблиці 3.1.
, яку завод може щомісячно виділяти в обмеженій кількості. Кількість сировини кожного виду, необхідної для виготовлення кожного виду продукції, ціна кожного виду продукції, а також лімітоване щомісячне надходження потрібної сировини подано в таблиці 3.1.

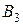





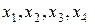 відповідно ті кількості продукції асортиментів
відповідно ті кількості продукції асортиментів  умовних одиниць сировини
умовних одиниць сировини  ; на випуск
; на випуск  , на випуск
, на випуск  , на випуск
, на випуск 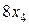 умовних одиниць сировини
умовних одиниць сировини  .
.


 .Аналогічні міркування приводять до такої системи лінійних нерівностей, які накладають обмеження на значення змінних
.Аналогічні міркування приводять до такої системи лінійних нерівностей, які накладають обмеження на значення змінних 

 ), очевидно визначається так:
), очевидно визначається так: 
 . Трапляються задачі, де значення змінних задовольняють систему нерівностей лише виду
. Трапляються задачі, де значення змінних задовольняють систему нерівностей лише виду  , або систему лінійних рівнянь, або мішану систему рівнянь і нерівностей.
, або систему лінійних рівнянь, або мішану систему рівнянь і нерівностей. будь-яке із трьох співвідношень:
будь-яке із трьох співвідношень:  , то математичну модель загальної задачі лінійного програмування можна подати в такому вигляді: знайти такі числові значення змінних
, то математичну модель загальної задачі лінійного програмування можна подати в такому вигляді: знайти такі числові значення змінних  які задовольняють систему лінійних обмежень:
які задовольняють систему лінійних обмежень:
 .
. , то це те саме, що шукати мінімум функції
, то це те саме, що шукати мінімум функції  .
.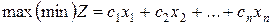 (3.1)
(3.1) (3.2)
(3.2) . (3.3)
. (3.3) , які задовольняють умови (3.2) і (3.3), і цільова функція (3.1) набуває екстремального (максимального чи мінімального) значення.
, які задовольняють умови (3.2) і (3.3), і цільова функція (3.1) набуває екстремального (максимального чи мінімального) значення. , координати якого задовольняють систему обмежень (3.2) та умови невід’ємності змінних (3.3), називається допустимим розв’язком (планом) задачі лінійного програмування.
, координати якого задовольняють систему обмежень (3.2) та умови невід’ємності змінних (3.3), називається допустимим розв’язком (планом) задачі лінійного програмування. лінійно незалежних обмежень системи (3.2) у вигляді рівностей, а також обмеження (3.3) щодо невід’ємності змінних.
лінійно незалежних обмежень системи (3.2) у вигляді рівностей, а також обмеження (3.3) щодо невід’ємності змінних. , за якого цільова функція (3.1) досягає максимального (чи мінімального) значення, називається оптимальним розв’язком (планом) задачі лінійного програмування.
, за якого цільова функція (3.1) досягає максимального (чи мінімального) значення, називається оптимальним розв’язком (планом) задачі лінійного програмування. , або
, або  .
.
 невід’ємні, а всі обмеження є рівностями.
невід’ємні, а всі обмеження є рівностями. -те обмеження на -1, дістанемо у правій частині відповідної рівності додатне значення. Коли
-те обмеження на -1, дістанемо у правій частині відповідної рівності додатне значення. Коли 
 :
: .
.
 :
: ,
,



