
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Економічна і математична постановки транспортної задачіСодержание книги
Поиск на нашем сайте
Класична транспортна задача лінійного програмування формулюється так: деякий однорідний продукт, що знаходиться у m постачальників А Необхідно визначити план перевезень, за якого вся продукція була б вивезена від постачальників, повністю задоволені потреби споживачів і загальна вартість всіх перевезень була б мінімальною. У такій постановці задачі ефективність плану перевезень визначається його вартістю і така задача має назву транспортної задачі за критерієм вартості перевезень. Запишемо її математичну модель. Позначимо через Таблиця 7.1.
Мають виконуватися такі умови: 1) сумарний обсяг продукції, що вивозиться з кожного
2) сумарний обсяг продукції, що ввезений кожному
3) сумарна вартість всіх перевезень повинна бути мінімальною:
У скороченій формі запису математична модель транспортної задачі за критерієм вартості перевезень має такий вигляд:
за обмежень:
У розглянутій задачі має виконуватися умова:
Транспортну задачу називають збалансованою, або закритою, якщо виконується умова (7.5). Якщо ж така умова не виконується, то транспортну задачу називають незбалансованою, або відкритою. Планом транспортної задачі називають будь-який невід'ємний розв'язок системи обмежень (7.2)—(7.4), який позначають матрицею Оптимальним планом транспортної задачі називають матрицю Теорема (умова існування розв'язку транспортної задачі): необхідною і достатньою умовою існування розв'язку транспортної задачі(7.1)—(7.4) є її збалансованість: Доведення. Необхідність. Нехай задача (7.1)—(7.4) має розв'язок
Оскільки ліві частини рівнянь (7.6) та (7.7) збігаються, то праві також рівні одна одній, отже, виконується умова:
Достатність. Потрібно показати, що за заданої умови (7.8) існує хоча б один план задачі, і цільова функція на множині планів обмежена. Нехай
Оскільки умови (7.2) та (7.3) виконуються, то Виберемо з елементів Виберемо з елементів Тобто цільова функція на множині допустимих планів транспортної задачі є обмеженою: Якщо при перевірці збалансованості (7.5) виявилося, що транспортна задача є відкритою, то її необхідно звести до закритого типу. Це здійснюється введенням фіктивного (умовного) постачальника Вартість перевезення одиниці продукції від фіктивного постачальника Як згадувалося вище, транспортна задача (7.1)-(7.4) є звичайною задачею лінійного програмування і може бути розв'язана симплексним методом, однак особливості побудови математичної моделі транспортної задачі дають змогу розв'язати її простіше. Легко помітити, що всі коефіцієнти при змінних у рівняннях (7.2), (7.3) дорівнюють одиниці, а сама система обмежень (7.2), (7..3) задана в канонічній формі. Крім того, система обмежень (7.2), (7.3) складається з mn невідомих та m+n рівнянь, які пов'язані між собою співвідношенням (7.8). Якщо додати відповідно праві та ліві частини систем рівнянь (7.2) та (7.3), то отримаємо два однакових рівняння:
Наявність у системі обмежень двох однакових рівнянь свідчить про її лінійну залежність. Якщо одне з цих рівнянь відкинути, то в загальному випадку система обмежень буде містити 7.2. Методи побудови опорного плану транспортної задачі Як і в звичайному симплексному методі, розв'язування транспортної задачі полягає в цілеспрямованому переборі та перевірці на оптимальність опорних планів. Початком такого ітераційного процесу є побудова першого опорного плану. Розглянемо методи північно-західного кута, мінімальної вартості, подвійної переваги та метод апроксимації Фотеля. Побудову опорного плану зручно подавати у вигляді таблиці, в якій постачальники продукції відповідають рядкам, а споживачі-стовпчикам. Нехай умови конкретної транспортної задачі подані в табл. 7.2.1. Таблиця 7.2.1.
Ідея методу північно-західного кута полягає в тому, що заповнення таблиці починають не враховуючи вартостей перевезень, з лівого верхнього (північно-західного) кута. У клітину записують менше з двох чисел Розглянемо цей процес детальніше на прикладі. Спочатку, не враховуючи вартості перевезень, завжди задовольняють потреби першого споживача Таблиця 7.2.2
Отже, в таблиці 7.2.2 у заповнених клітинках знаходяться числа, що означають можливий план перевезень продукції. Сума чисел (перевезень) по рядках дорівнює обсягам запасів постачальників, а сума чисел по стовпцях — обсягам потреб відповідних споживачів. Аналогічний результат можна отримати, якщо почати з правого нижнього кута таблиці, рухаючись до лівого верхнього. Процедуру методу можна застосовувати також, починаючи розподіл поставок з лівого нижнього кута і рухаючись до правого верхнього по діагоналі. В такому разі спосіб розподілу перевезень можна було б назвати методом південно-західного кута, тому цей метод ще називають діагональним. Метод північно-західного кута є найпростішим, однак і найменш ефективним. Процес відшукання оптимального плану після початкового опорного, визначеного методом північно-західного кута, пов'язаний зі значним обсягом обчислювальних робіт, тому його реалізують на ЕОМ. Визначимо загальну вартість перевезень згідно з початковим опорним планом. Від першого постачальника до першого споживача необхідно перевезти 110 одиниць продукції за ціною 4 ум. од. (ціна записана в правому верхньому куті кожної клітини), отже коштуватиме Якщо за побудови опорного плану враховувати вартості перевезень, то сумарна вартість всіх постачань може бути зменшена, і отриманий опорний план буде ближчим до оптимального. Ідея методу мінімальної вартості полягає в тому, що на кожному кроці заповнюють клітинку таблиці, яка має найменшу вартість перевезення одиниці продукції. Такі дії повторюють доти, доки не буде розподілено всю продукцію між постачальниками та споживачами. Складемо за допомогою цього методу план розглянутої задачі (табл. 7.2.3). Найменшу вартість мають перевезення, які здійснюються від З клітинок таблиці, що залишились незаповненими, вибираємо наступне мінімальне значення вартості перевезень, яке дорівнює 2 ум.од. - для клітин Заповнення клітин Знову вибираємо найменшу вартість для клітин таблиці, що залишилися пустими, і продовжуємо процес доти, поки всі запаси не будуть розподілені, а потреби — задоволені. В результаті таких міркувань отримали початковий опорний план, загальна вартість перевезень для якого становить:
Значення цільової функції менше за попередній варіант, значить цей план ближчий до оптимального. Таблиця 7.2.3.
Метод подвійної переваги. Якщо розмірність задачі досить велика, то перебір за методом мінімальної вартості ускладнюється. В такому разі спростити пошук клітин з найменшими вартостями можна, застосовуючи метод подвійної переваги. Згідно з процедурою цього методу перед початком заповнення таблиці необхідно позначити будь-якими символами клітинки, які містять найменшу вартість у рядках, а потім — у стовпчиках. Таблицю починають заповнювати з клітинок, позначених двічі (які містять вартості, що є мінімальними і в рядку, і в стовпчику). Далі заповнюють клітинки, позначені один раз (що містять мінімальні вартості або в рядку, або в стовпчику), а вже потім — за методом мінімальної вартості. Таблиця 7.2.4
Застосування для побудови опорного плану даного методу уможливлює отримання найменшого у зіставленні з розглянутими вище значення цільової функції. Отже, такий план є найближчим до оптимального. Метод апроксимації Фогеля. За цим методом на кожному кроці визначають різницю між двома найменшими вартостями в кожному рядку і стовпчику транспортної таблиці. Ці різниці записують у спеціально відведених місцях таблиці — знизу та справа у кілька рядків та стовпчиків, що відповідають крокам заповнення таблиці. З-поміж усіх різниць вибирають найбільшу і у відповідному рядку чи стовпчику заповнюють клітинку з найменшою вартістю. Якщо ж однакових найбільших різниць кілька, то вибирають будь-який відповідний рядок або стовпчик. Коли залишається незаповненим лише один рядок або стовпчик, то обчислення різниць припиняють, а таблицю продовжують заповнювати за методом мінімальної вартості. Даний метод побудови опорного плану враховує не лише маршрути з мінімальними витратами перевезень продукції, але й співвідношення витрат у рядку чи стовпчику, тобто розраховується наскільки, може збільшитися вартість постачання на наступних кроках процедури, якщо не здійснити на поточному кроці постачання в клітину з мінімальною вартістю. Метод апроксимації Фогеля дає змогу особливо для задач великих розмірностей скласти найкращий опорний план. У таблиці 7.2.5 напроти кожного рядка і стовпчика записані величини, які знайдені як різниці між мінімальним значенням вартості та наступним за ним по рівню. Максимальне значення такої різниці на першому кроці відповідає четвертому стовпчику і означає, що у разі, коли не буде задоволена потреба четвертого споживача перевезенням продукції від третього постачальника за ціною 2 ум. од. за одиницю, то на наступних кроках вартість перевезення може бути на 3 ум. од. більшою. Тобто інакше може статися, що потребу четвертого споживача необхідно буде задовольняти перевезенням продукції від першого постачальника, що призведе до збільшення вартості цього перевезення в 2,5 рази. Водночас для всіх інших споживачів та постачальників такі різниці є меншими. Отже, найдоцільніше на першому кроці заповнити клітину Таблиця 7.2.5.
На другому кроці максимальна різниця дорівнює 2 і відповідає першому і другому рядкам та першому і другому стовпчикам, тому можна заповнювати будь-яку їх клітину з мінімальною вартістю, наприклад, Останній розрахунок різниць (найбільше значення 3 відповідає другому стовпчику) свідчить про доцільність введення поставки від третього постачальника до другого споживача. Решту клітин заповнимо методом мінімальної вартості та визначимо загальну вартість перевезень:
Результат збігся із значенням цільової функції для опорного плану, що складений за попереднім методом. Ефективність методу апроксимації Фогеля є очевидною для задач більшої розмірності. Ефективність наведених методів можна оцінювати лише в середньому, оскільки можлива ситуація, що методом мінімальної вартості отримано опорний план транспортної задачі кращий, ніж методом подвійної переваги.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 740; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.009 с.) |

 в обсягах
в обсягах 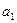 ,
,  ,…,
,…,  одиниць відповідно необхідно перевезти n споживачам
одиниць відповідно необхідно перевезти n споживачам  в обсягах
в обсягах  ,
,  ,…,
,…,  одиниць. При цьому виконується умова, що загальний наявний обсяг продукції у постачальників дорівнює загальному попиту всіх споживачів. Відомі вартості
одиниць. При цьому виконується умова, що загальний наявний обсяг продукції у постачальників дорівнює загальному попиту всіх споживачів. Відомі вартості 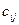 перевезень одиниці продукції від кожного
перевезень одиниці продукції від кожного 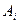 -го постачальника до кожного
-го постачальника до кожного  .
. обсяг продукції, що перевозиться від
обсяг продукції, що перевозиться від 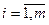 ;
;  ). Тоді умови задачі зручно подати у вигляді такої таблиці:
). Тоді умови задачі зручно подати у вигляді такої таблиці:
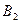



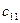
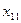
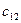
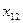
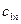
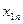
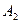

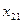
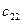
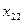

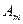
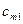
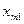
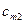



 -го пункту, має дорівнювати запасу продукції в даному пункті:
-го пункту, має дорівнювати запасу продукції в даному пункті:
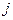 -му споживачеві, має дорівнювати його потребам:
-му споживачеві, має дорівнювати його потребам:
 Очевидно, що
Очевидно, що  .
.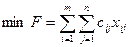 (7.1)
(7.1)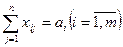 ; (7.2)
; (7.2) ; (7.3)
; (7.3)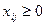 (
( . (7.5)
. (7.5) (
(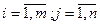 ). Значення невідомих величин
). Значення невідомих величин  (
(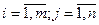 ), яка задовольняє умови задачі, і для якої цільова функція (7.1) набирає найменшого значення.
), яка задовольняє умови задачі, і для якої цільова функція (7.1) набирає найменшого значення. .
. , тоді для нього виконуються рівняння-обмеження (7.2) і (7.3). Підсумуємо відповідно ліві та праві частини систем рівнянь (7.2) і (7.3). Матимемо:
, тоді для нього виконуються рівняння-обмеження (7.2) і (7.3). Підсумуємо відповідно ліві та праві частини систем рівнянь (7.2) і (7.3). Матимемо: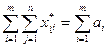 , (7.6)
, (7.6)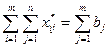 . (7.7)
. (7.7)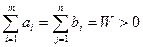 . Розглянемо величину
. Розглянемо величину  (
( ;
; .
. . Якщо замінити в цільовій функції (7.1) всі коефіцієнти на
. Якщо замінити в цільовій функції (7.1) всі коефіцієнти на  , то, враховуючи (7.2), матимемо:
, то, враховуючи (7.2), матимемо:  .
. . Якщо замінити в цільовій функції (7.1) всі коефіцієнти на
. Якщо замінити в цільовій функції (7.1) всі коефіцієнти на 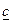 , то, враховуючи (7.2), матимемо:
, то, враховуючи (7.2), матимемо: 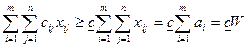 .
. . Теорему доведено.
. Теорему доведено. у разі перевищення загального попиту над запасами (
у разі перевищення загального попиту над запасами ( ), із ресурсом обсягом
), із ресурсом обсягом 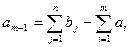 . Якщо ж загальні запаси постачальників перевищують попит споживачів (
. Якщо ж загальні запаси постачальників перевищують попит споживачів ( ), то до закритого типу задача зводиться введенняь фіктивного (умовного) споживача
), то до закритого типу задача зводиться введенняь фіктивного (умовного) споживача 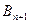 з потребою
з потребою 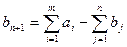 .
.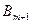 ) до кожного зі споживачів (виробників) має дорівнювати нулю або бути набагато більшою за реальні витрати
) до кожного зі споживачів (виробників) має дорівнювати нулю або бути набагато більшою за реальні витрати 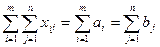 ;
; .
. лінійно незалежне рівняння, отже, їх можна розв'язати відносно
лінійно незалежне рівняння, отже, їх можна розв'язати відносно 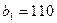 , а запаси постачальника -
, а запаси постачальника - 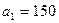 одиниць (тобто із запасів першого постачальника можна повністю задовольнити потреби першого споживача), тому в клітину
одиниць (тобто із запасів першого постачальника можна повністю задовольнити потреби першого споживача), тому в клітину 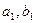 , тобто 110. Тепер потреби першого споживача повністю задоволені, і переходимо до задоволення потреб наступного (другого) споживача
, тобто 110. Тепер потреби першого споживача повністю задоволені, і переходимо до задоволення потреб наступного (другого) споживача 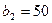 . Після задоволення потреб першого споживача залишок запасів першого постачальника становить
. Після задоволення потреб першого споживача залишок запасів першого постачальника становить 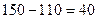 . Отже, від першого виробника другому споживачеві можна перевезти лише 40 одиниць продукції, тому в клітину
. Отже, від першого виробника другому споживачеві можна перевезти лише 40 одиниць продукції, тому в клітину  , а незадоволені потреби другого споживача
, а незадоволені потреби другого споживача 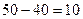 , тому в клітинку
, тому в клітинку 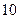 , і другий споживач у такий спосіб також повністю отримав необхідну кількість продукції. Переходимо до задоволення потреб наступного споживача
, і другий споживач у такий спосіб також повністю отримав необхідну кількість продукції. Переходимо до задоволення потреб наступного споживача 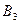 . У результаті часткового використання запасів другого постачальника його залишок продукції становить
. У результаті часткового використання запасів другого постачальника його залишок продукції становить 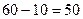 . Отже, від другого виробника до третього споживача можна перевезти
. Отже, від другого виробника до третього споживача можна перевезти 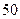 одиниць продукції. Клітинка
одиниць продукції. Клітинка  . Залишились незадоволеними потреби третього споживача в обсязі
. Залишились незадоволеними потреби третього споживача в обсязі 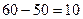 . Для їх задоволення скористаємося запасами постачальника
. Для їх задоволення скористаємося запасами постачальника  , з потребами
, з потребами  , які повністю задовольняються за рахунок залишку запасів третього постачальника:
, які повністю задовольняються за рахунок залишку запасів третього постачальника: 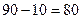 .
.
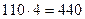 ум. од. Крім того, необхідно перевезти від першого постачальника 40 одиниць продукції до другого споживача за ціною 4 ум. од. і т. д. У такий спосіб визначимо загальну вартість усіх перевезень:
ум. од. Крім того, необхідно перевезти від першого постачальника 40 одиниць продукції до другого споживача за ціною 4 ум. од. і т. д. У такий спосіб визначимо загальну вартість усіх перевезень: 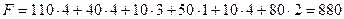 (ум. од.).
(ум. од.).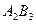 . Оскільки постачальник має 60 одиниць продукції, а споживач потребує саме такої її кількості, то в клітину
. Оскільки постачальник має 60 одиниць продукції, а споживач потребує саме такої її кількості, то в клітину 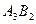 .
. ,
, 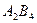 ,
, 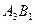 та
та  .
. , причому 50 одиниць продукції вже надано другому споживачеві. Отже, маємо залишок
, причому 50 одиниць продукції вже надано другому споживачеві. Отже, маємо залишок 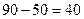 , а потреби
, а потреби 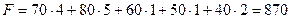 (ум. од.).
(ум. од.).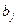

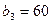
 (ум.од.).
(ум.од.).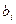
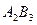 . Після цього з розгляду виключаються одразу всі клітини другого рядка та третього стовпця, оскільки потреби третього споживача повністю задоволені, а запаси другого і постачальника вичерпані.
. Після цього з розгляду виключаються одразу всі клітини другого рядка та третього стовпця, оскільки потреби третього споживача повністю задоволені, а запаси другого і постачальника вичерпані. (ум.од.).
(ум.од.).


