
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Симплексний метод розв'язування задач лінійного програмуванняСодержание книги
Поиск на нашем сайте
Графічний метод для визначення оптимального плану задач лінійного програмування доцільно застосовувати лише для задач із двома змінними. За більшої кількості змінних необхідно застосовувати інший метод. З властивостей розв'язків задачі лінійного програмування відомо: оптимальний розв'язок задачі має знаходитись в одній з кутових точок багатогранника допустимих розв'язків. Тому найпростіший спосіб відшукання оптимального плану потребує перебору всіх кутових точок (допустимих планів задачі, які ще називають опорними). Порівняння вершин багатогранника можна здійснювати тільки після відшукання якоїсь однієї з них, тобто знайшовши початковий опорний план. Кожний опорний план визначається системою m лінійно незалежних векторів, які містяться в системі обмежень задачі з n векторів Ідея цього методу полягає в здійсненні спрямованого перебору допустимих планів у такий спосіб, що на кожному кроці здійснюється перехід від одного опорного плану до наступного, який за значенням цільової функції був би хоча б не гіршим за попередній. Значення функціонала при переході змінюється в потрібному напрямку: збільшується (для задачі на максимум) чи зменшується (для задачі на мінімум). Процес розв'язання задачі симплекс-методом має ітераційний характер: однотипні обчислювальні процедури (ітерації) повторюються у певній послідовності доти, доки не буде отримано оптимальний план задачі або з'ясовано, що його не існує. Отже, симплекс-метод — це ітераційна обчислювальна процедура, яка дає змогу, починаючи з певного опорного плану, за скінченну кількість кроків отримати оптимальний план задачі лінійного програмування. 5.1. Початковий опорний план Розглянемо задачу лінійного програмування, записану в канонічній формі:
Не порушуючи загальності, допустимо, що система рівнянь містить перші m одиничних векторів. Отримаємо:
Система обмежень (5.1.2) у векторній формі матиме вигляд:
де
тобто допустимий план. Такому плану відповідає розклад
де 5.2. Оптимальний розв’язок. Критерій оптимальності плану Симплексний метод уможливлює направлений перебір опорних планів, тобто перехід від одного плану до іншого, який є хоча б не гіршим від попереднього за значенням функціонала. Отже, окремим питанням стає вибір вектора, який необхідно вводити в базис при здійсненні ітераційної процедури симплексного методу. Розглянемо задачу лінійного програмування (5.1.1)-(5.1.3). Допустимо, що вона має опорні плани і вони є не виродженими. Розглянемо початковий опорний план виду (5.1.5), якому відповідає розклад за базисними векторами (5.1.6) та значення функціонала
Кожен з векторів
тому такому розкладу відповідатиме і єдине значення функціонала:
Позначимо через
то план Аналогічно формулюється умова оптимальності плану задачі на відшукання мінімального значення функціонала: якщо для деякого плану
то план Отже, для того щоб план задачі лінійного програмування був оптимальним, необхідно і достатньо, щоб його оцінки Умови оптимальності планів задач лінійного програмування є наслідками двох теорем (наведемо їх без доведень). Теорема 5.2.1. Якщо для деякого вектора Теорема 5.2.2. Якщо для деякого вектора
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.44.171 (0.005 с.) |

 . Отже, загальна кількість опорних планів визначаєтьсякількістю комбінацій
. Отже, загальна кількість опорних планів визначаєтьсякількістю комбінацій  . Задачі, що описують реальні економічні процеси, мають велику розмірність, і простий перебір всіх опорних планів таких задач є дуже складним, навіть за умови застосування сучасних ЕОМ. Тому необхідне використання методу, який уможливлював би скорочення кількості обчислень. 1949 року такий метод був запропонований американським вченим Дж.Данцігом — так званий симплексний метод, або симплекс-метод.
. Задачі, що описують реальні економічні процеси, мають велику розмірність, і простий перебір всіх опорних планів таких задач є дуже складним, навіть за умови застосування сучасних ЕОМ. Тому необхідне використання методу, який уможливлював би скорочення кількості обчислень. 1949 року такий метод був запропонований американським вченим Дж.Данцігом — так званий симплексний метод, або симплекс-метод. ,
,

 (5.1.2)
(5.1.2) , (5.1.4)
, (5.1.4) ,
,  ,…,
,…,  ,
,  , …,
, …,  ,
,  ,
, - лінійно незалежні одиничні вектори m -вимірного простору, що утворюють одиничну матрицю і становлять базис цього простору. Тому в розкладі (5.1.4) базисними змінними будуть
- лінійно незалежні одиничні вектори m -вимірного простору, що утворюють одиничну матрицю і становлять базис цього простору. Тому в розкладі (5.1.4) базисними змінними будуть 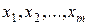 , а інші змінні – вільні. Прирівняємо всі вільні змінні до нуля, тобто
, а інші змінні – вільні. Прирівняємо всі вільні змінні до нуля, тобто  . Оскільки
. Оскільки  , а вектори
, а вектори 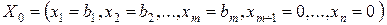 , (5.1.5)
, (5.1.5) , (5.1.6)
, (5.1.6) є кутовою точкою багатогранника розв’язків, а отже, може бути початковим опорним планом.
є кутовою точкою багатогранника розв’язків, а отже, може бути початковим опорним планом. .
. ,
, .
. коефіцієнт функціонала, що відповідає вектору
коефіцієнт функціонала, що відповідає вектору  , та
, та  (їх називають оцінками відповідних векторів плану)
(їх називають оцінками відповідних векторів плану)  . Тоді справедливим є таке твердження (умова оптимальності плану задачі лінійного програмування): якщо для деякого плану
. Тоді справедливим є таке твердження (умова оптимальності плану задачі лінійного програмування): якщо для деякого плану 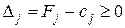 ,
, ,
, , то план
, то план  .
. , то план
, то план  .
.


