
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Економічна постановка і математична модель задачі нелінійного програмування
Досить детально розглянута в розділах, присвячених лінійному програмуванню, задача пошуку оптимальних обсягів виробництва ґрунтується на припущеннях про лінійність зв’язку між витратами ресурсів і обсягами виготовленої продукції; між ціною, рекламою та попитом тощо. Якщо такі зв’язки насправді є нелінійними, то більш адекватні математичні моделі доцільно формулювати в термінах нелінійного програмування. Нехай для деякої виробничої системи необхідно визначити план випуску продукції, за умови найкращого способу використання ресурсів системи. Відомі загальні запаси кожного ресурсу, нормативи витрат кожного ресурсу на одиницю продукції та ціна реалізації одиниці виготовленої продукції. Критерії оптимальності можуть бути різноманітними, наприклад максимізація виручки від реалізації продукції. Така умова подається лінійною залежністю загальної виручки від обсягів проданого товару та ціни одиниці продукції. Однак, загально відомим є факт, що за умов ринкової конкуренції питання реалізації продукції є досить складним. Обсяг збуту кінцевої продукції визначається перш за все її ціною, отже в якості цільової функції доцільно розглядати максимізацію не всієї виготовленої, а лише реалізованої продукції. Тоді необхідно визначити також і оптимальне значення ціни одиниці продукції при якій обсяг збуту буде максимальним, для цього її потрібно ввести в задачу як невідому величину, при цьому обмеження задачі мають враховувати зв’язки між ціною, рекламою та обсягами збуту продукції. Цільова функція міститиме добуток двох невідомих величин (оптимальна ціна одиниці продукції та оптимальна кількість відповідного виду продукції) отже є нелінійною. Таким чином маємо задачу нелінійного програмування. І нарешті будь-яка задача стає нелінійною, якщо в математичній моделі необхідно враховувати умови невизначеності та ризик. В якості величини ризику розповсюджене використання такої величини як дисперсія, тому врахування обмеженості ризику вимагає введення нелінійної функції в систему обмежень, а мінімізація ризику певного процесу досягається за рахунок дослідження математичної моделі з нелінійною цільовою функцією. Загальна задача математичного програмування формулюється наступним чином:
Знайти такі значення змінних xj за умов
Якщо всі функції
5.10. Геометрична інтерпретація задачі нелінійного програмування Геометрично цільова функція (5.33) визначає деяку поверхню, обмеження (5.34)-(5.35) визначають допустиму підмножину n -вимірного евклідового простору. Знаходження оптимального розв’язку задачі нелінійного програмування зводиться до відшукання точки з допустимої підмножини, в якій досягається поверхня найвищого (найнижчого) рівня. Якщо цільова функція неперервна, а допустима множина розв’язків замкнена, не пуста і обмежена, то глобальний максимум (мінімум) задачі існує. Найпростішими для розв’язування є задачі нелінійного програмування, що містять систему лінійних обмежень та нелінійну цільову функцію. В цьому випадку область допустимих розв’язків є опуклою, тобто замкненою, непустою та обмеженою. Розглянемо приклад геометричного способу розв’язування задачі нелінійного програмування. Приклад 5.5. Знайти мінімальне і максимальне значення функції
за умов
Розв’язування. Область допустимих розв’язків утворює чотирикутник АВСD (рис. 5.7). Геометрично цільова функція представляє коло з центром в точці М (2; 2) і квадратом радіуса
Оскільки Очевидно, що найменший радіус Відмітимо, що в даному випадку точка, яка відповідає оптимальному плану задачі знаходиться всередині багатокутника допустимих розв’язків, що для задач лінійного програмування неможливо.
Множники Лагранжа Для розв'язування задач нелінійного програмування не існує універсального методу, а тому доводиться застосовувати багато методів іобчислювальних алгоритмів, які ґрунтуються, здебільшого, на теорії диференціального числення, і вибір їх залежить від конкретної постановки задачі та форми економіко-математичної моделі. Методи нелінійного програмування бувають прямі та непрямі. Прямими методами оптимальні розв'язки відшукують у напрямку найшвидшого збільшення (зменшення) цільової функції. Типовими для цієї групи методів є градієнти. Непрямі методи полягають у зведенні задачі до такої, знаходження оптимуму якої вдається спростити. До них належать, насамперед, найбільш розроблені методи квадратичного та сепарабельного програмування. Оптимізаційні задачі, на змінні яких не накладаються обмеження, розв'язують методами класичної математики. Оптимізацією з обмеженнями-рівностями виконують методами зведеного градієнта, скажімо методом Якобі, та множників Лагранжа. У задачах оптимізації з обмеженнями-нерівностями досліджують необхідні та достатні умови існування екстремуму Куна—Таккера. Розглянемо метод множників Лагранжа на прикладі такої задачі нелінійного програмування: Z =f (х1, х2... хп) — > mах (min) за умов q1(x1,x2,…xn)=bi,i=1, де функція f (х1, x2,..., хп) i q1(x1, x2, …xn) диференційовані. Ідея методу множників Лагранжа полягає в заміні даної задачі простішою: на знаходження екстремуму складнішої функції, але без обмежень. Ця функція називається функцією Лагранжа і подається у вигляді
де λi— не визначені поки що величини, так звані множники Лагранжа. Знайшовши частинні похідні функції L за всіма змінними і прирівнявши їх до нуля:
запишемо систему
що є, як правило, нелінійною. Розв'язавши цю систему, знайдемо X* =(х1, x2,..., хп) i λ0= (λ1, λ 2,..., λm) — стаціонарні точки. Оскільки їх визначено з необхідної умови екстремуму, то в них можливий максимум або мінімум. Іноді стаціонарна
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.61.223 (0.009 с.) |
 , щоб цільова функція набувала екстремального (максимального чи мінімального значення):
, щоб цільова функція набувала екстремального (максимального чи мінімального значення):  (5.33)
(5.33)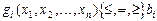 (
( )(5.34)
)(5.34)
 (5.35)
(5.35)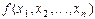 та
та 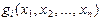 (
( ) є лінійними, то приходимо до задачі лінійного програмування, інакше (хоча б одна з функцій не є лінійною) маємо задачу нелінійного програмування.
) є лінійними, то приходимо до задачі лінійного програмування, інакше (хоча б одна з функцій не є лінійною) маємо задачу нелінійного програмування.


 , тобто значення цільової функції буде збільшуватися (зменшуватися) зі збільшенням (зменшенням) радіусу кола. Проведемо з точки М кола різних радіусів. Функція Z має два локальних максимуми: точка В (0; 6) і С (8; 0). Обчислимо значення функціоналу в цих точках:
, тобто значення цільової функції буде збільшуватися (зменшуватися) зі збільшенням (зменшенням) радіусу кола. Проведемо з точки М кола різних радіусів. Функція Z має два локальних максимуми: точка В (0; 6) і С (8; 0). Обчислимо значення функціоналу в цих точках: ,
,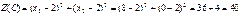 .
. , то точка С (8; 0) – точка глобального максимуму.
, то точка С (8; 0) – точка глобального максимуму. , тоді
, тоді  . Тобто точка М є точкою мінімуму, оскільки їй відповідає найменше можливе значення цільової функції.
. Тобто точка М є точкою мінімуму, оскільки їй відповідає найменше можливе значення цільової функції.





