
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение границ устойчивости двойственных оценок.Содержание книги
Поиск на нашем сайте
1 Нахождение интервалов устойчивости двойственной оценки по отношению к изменениям ресурсов каждого типа
если
Очевидно если Далее если
если
если III тип ресурса принадлежит соответственно Если найдено решение задачи, то нетрудно провести анализ устойчивости двойственных оценок относительно изменений 1. проанализировать устойчивость оптимального плана задачи, относительно изменений свободных членов системы линейных уравнений 2. оценить степень влияния изменения 30) Экономические примеры, математическая постановка задачи целочисленного программирования. Целочисленное программирование — разновидность математического программирования, подразумевающая, что искомые значения должны быть целыми числами. Раздел математического программирования, в котором изучаются методы нахождения экстремумов функций в пространстве параметров, где все или некоторые переменные являются целыми числами. Простейший метод решения задачи целочисленного программирования — сведение её к задаче линейного программирования с проверкой результата на целочисленность. В математической модели задачи целочисленного программирования как целевая функция, так и функции в системе ограничений могут быть линейными, нелинейными и смешанными .
Составление дополнительных ограничений Составление дополнительного ограничения (сечения) и решение расширенной задачи обычным симплекс-методом. Дополнительное ограничение (сечение) отсекает нецелочисленные решения. Сечение обладает следующими двумя свойствами: 1) любое целочисленное решение ему удовлетворяет;
2) любое не целочисленное решение задачи ему не удовлетворяет. Объясним, как составляется сечение. Пусть выполнен этап 1; Рассмотрим i -е ограничение: bi = xi +aim+lxm+1 +aim+2xm+2+…+ainxn. Так как bi – дробное, а в пра вой ча сти все переменные целые, хотя бы одно значение aij, Возьмем дробную часть от левой и правой частей ограничения. Обозначим через { r } дробную часть числа r. Дробная часть суммы не превосходит суммы дробных частей слагаемых, поэтому Дробная часть произведения не превосходит произведения целого на дробную часть, следовательно: В результате имеем Обозначим Тогда из последнего неравенства получаем Отняв от левой части неравенства дополнительную неотрицательную переменную, переходим к уравнению При дополнении этого ограничения к исходной задаче мы по лучили задачу большей размерности. Эту задачу решают обычным симплекс-методом, т. е.. переходя к этапу 1. Если при решении задачи симплекс-методом имеется несколько дробных решений, то дополнительные ограничения следует составлять для значения, имеющего максимальную дробную часть. Метод Гомори С помощью отсечений выделяют целочисленные части полиэдров. Метод отсечений был разработан в конце 1950-х годов Гомори для решения целочисленных линейных программ с помощью симплекс-метода. Метод отсечений оказался полезным и с теоретической точки зрения он дает возможность описать целочисленную оболочку полиэдра. Далее описывается метод отсечений Гомори, дающий алгоритм решения задач целочисленного линейного программирования. Данный метод, который также носит название метода отсекающих плоскостей, предназначен для решения ЦЗЛП (целочисленной задачи линейного программирования) в канонической форме. Описываемая ниже версия алгоритма предназначена для решения полностью целочисленных задач, т.е. таких, у которых все параметры aij, cj, bi – целые. Описание алгоритма. Приведем обобщенную схему алгоритма Гомори. Структурно он делится на так называемые большие итерации. Каждая большая итерация содержит этапы: 1. Сначала задача решается методами линейного программирования (малые итерации), обычно симплекс-методом, и анализируется результат, если результатом являются целые числа, то на этом решение заканчивается, а если дробные, то производят следующие операции:
2. В оптимальном плане (симплекс-таблице) выбирают строку, в которой целая часть дробного(!) свободного члена (P0) принимает наибольшее значение. 3. Построение для найденной компоненты условия отсечения. 4. Переход на начало следующей большой итерации. Замечание: При добавлении в симплекс-таблицу нового базисного вектора по новой переменной xn+1 мы получаем недопустимое (отрицательное) решение. Для того, чтобы избавиться от недопустимого решения выбираем столбец замещения так, чтобы строкойзамещения стала новая добавленная строка по переменной xn+1. Продолжаем пересчет симплекс-таблицы. Если снова получаем дробное решение, то еще вводим дополнительный базисный вектор, и так до получения целочисленного решения.Но следует заметить, что если область допустимых решений очень мала, то она может и не содержать целых значений, это необходимо проверить графически. Если область допустимых решений не содержит целочисленного решения, то в применении метода Гомори нет необходимости, целого решения не будет!
Метод ветвей и границ Впервые метод ветвей и границ был предложен Лендом и Дойгом [1] в 1960 для решения общей задачи целочисленного линейного программирования. Интерес к этому методу и фактически его “второе рождение” связано с работой Литтла, Мурти, Суини и Кэрела [2], посвященной задаче комивояжера [3]. Начиная с этого момента, появилось большое число работ, посвященных методу ветвей и границ и различным его модификациям. Столь большой успех объясняется тем, что авторы первыми обратили внимание на широту возможностей метода, отметили важность использования специфики задачи и сами воспользовались спецификой задачи коммивояжера. В основе метода ветвей и границ лежит идея последовательного разбиения множества допустимых решений на подмножества (стратегия “разделяй и властвуй”). На каждом шаге метода элементы разбиения подвергаются проверке для выяснения, содержит данное подмножество оптимальное решение или нет. Проверка осуществляется посредством вычисления оценки снизу для целевой функции на данном подмножестве. Если оценка снизу не меньше рекорда — наилучшего из найденных решений, то подмножество может быть отброшено. Проверяемое подмножество может быть отброшено еще и в том случае, когда в нем удается найти наилучшее решение. Если значение целевой функции на найденном решении меньше рекорда, то происходит смена рекорда. По окончанию работы алгоритма рекорд является результатом его работы. Если удается отбросить все элементы разбиения, то рекорд — оптимальное решение задачи. В противном случае, из неотброшенных подмножеств выбирается наиболее перспективное (например, с наименьшим значением нижней оценки), и оно подвергается разбиению. Новые подмножества вновь подвергаются проверке и т.д.
Вычисление нижней границы является важнейшим элементом данной схемы. Для простейшей задачи размещения один из способов ее построения состоит в следующем. Запишем исходную задачу в терминах целочисленного линейного программирования [4]. Введем следующие переменные:
С использованием введенных
yi ³ xij, i Î I, j Î J, xij, yi, yi Î{0, 1}, i Î I, j Î J. Двойственная задача линейного программирования имеет вид:
vj £ gij + wij, i Î I, j Î J, wij ³0, i Î I, j Î J. Приближенное решение двойственной задачи используется в качестве нижней оценки. Для сокращения размерности задачи применяется так называемый блок предварительной отбраковки. Он основан на применении условий дополняющей нежесткости для задач линейного программирования
Если для оптимального решения двойственной задачи выражение в скобках положительно для некоторого i Î I, то “скорее всего” в исходной целочисленной задаче yi = 0, и размерность можно уменьшить. Понятно, что данный эвристический прием не всегда приводит к правильному решению. Поэтому в качестве порога лучше брать не 0, а некоторую величину d ³ 0, выбор которой зависит от исходных данных. Эту величину называют порогом отбраковки. Очевидно, что при d ³max ci, размерность задачи не сокращается. Другой способ уменьшения трудоемкости алгоритма состоит в искусственном завышении нижней оценки. Предположим, что нас интересует не только оптимальное решение, но и приближенные решения с относительной погрешностью не более e. Тогда завышение нижней оценки в (1 + e) раз приводит к желаемому результату.
ПРИЧИНЫ ВОЗНИКНОВЕНИЯ И ПРИМЕРЫ НЕЛИНЕЙНОСТЕЙ В ОПТИМИЗАЦИОННЫХ ЭКОНОМИЧЕСКИХ ЗАДАЧАХ Классификационный признак задач оптимизации — свойства функций f и множеств W. Например задачи называются линейными (часто говорят о задачах линейного программирования), если функция f — аффинная, а множество W — многогранное (множество W называется многогранным, если оно выделяется ограничениями с аффинными функциями g0 и g1). Если функции f, g0 и g1 квадратичные, то говорят о задачах квадратичного программирования или о квадратичных задачах оптимизации (условных или безусловных). Если эти функции выпуклые, то говорят о задачах выпуклого программирования (если множество W задается каким-либо другим образом, а не только ограничениями типа (4) и (5), то в задачах выпуклого программирования требуют его выпуклость). Наконец, в общем случае говорят о задачах нелинейного программирования. В таких задачах обычно предполагается гладкость фигурирующих в них функций.
Пример нелинейной задачи. Задачи о распределении ресурсов. Общий смысл таких задач — распределить ограниченный ресурс между потребителями оптимальным образом. Рассмотрим простейший пример — задачу о режиме работы энергосистемы. Пусть m электростанций питают одну нагрузку мощности p. Обозначим через xj активную мощность, генерируемую j-ой электростанцией. Техническими условиями определяются возможный минимум mj и максимум Mj вырабатываемой j-ой электростанцией мощности. Допустим затраты на генерацию мощности x на j-ой электростанции равны ej(x). Требуется сгенерировать требуемую мощность p при минимальных затратах. В наших обозначениях
Если обозначить
|
||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.37.217 (0.01 с.) |


 обратная матрицы В составленная из компонентов векторов
обратная матрицы В составленная из компонентов векторов  ,
,  ,
, 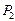 базиса, который определяет оптимальный план задачи взятых из столбцов векторов
базиса, который определяет оптимальный план задачи взятых из столбцов векторов  ,
, 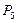 ,
,  образующий первоначальный единичный базис
образующий первоначальный единичный базис



 =
=  *
*  =
= 



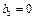
 это означает, что если количество ресурсов I типа будет увеличено в пределах 555,то несмотря на это оптимальным планом двойственной задачи остаётся план Y(0;5/2:1/2).
это означает, что если количество ресурсов I типа будет увеличено в пределах 555,то несмотря на это оптимальным планом двойственной задачи остаётся план Y(0;5/2:1/2).


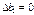

 , а количество остальных ресурсов остается первоначальным, то двойственная задача имеет один и тот же план.
, а количество остальных ресурсов остается первоначальным, то двойственная задача имеет один и тот же план. . Это, в свою очередь, позволяет:
. Это, в свою очередь, позволяет: , на максимальное значение целевой функции задачи, что дает возможность определить наиболее целесообразный вариант возможных изменений
, на максимальное значение целевой функции задачи, что дает возможность определить наиболее целесообразный вариант возможных изменений 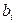 .
.
 – дробное число.
– дробное число. должно быть дробным.
должно быть дробным.




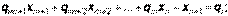


 обозначений простейшая задача размещения записывается следующим образом
обозначений простейшая задача размещения записывается следующим образом







 через
через  через W, то эта задача переписывается так
через W, то эта задача переписывается так



