
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 2. Інтерполяція функційСодержание книги
Поиск на нашем сайте
Задача інтерполювання Означення 1. Задачею інтерполяції (або інтерполювання) є побудова такої функції, яка для даних значень аргументу приймає задані значення. Нехай для значень аргументу х1, х2, …, хn, які називають вузлами інтерполяції, відомі значення деякої функції f (x): f (x0) = у0, f (x1) = у1, …, f (xn) = уn. Треба знайти інтерполюючу функцію Р(х), так, щоби у вузлах інтерполяції вона приймала ті ж самі значення, що й f (x), тобто Р(x0) = у0, Р(x1) = у1, …, Р(xn) = уn. Геометрично інтерполювання означає, що треба знайти криву Р(х), яка проходить через задані точки (х1;у1), (х2;у2), (х3;у3), … на графіку функції f (x).
у4 f (x)
х
Рисунок 1
Означення 2. Наближену рівність f (x) ≈ Рn(х) називають інтерполяційною формулою. Різницю Rn(f,x) = f (x) – Рn(х) називають залишковим членом інтерполяційної формули або похибкою інтерполювання. Серед методів інтерполювання найбільш розповсюдженим є лінійна інтерполяція, коли наближення шукають у вигляді Рn(х; а 0, а 1, …, а n) =
а 0 + а 1х1 + а 2 ...................... (1) а 0 + а 1хn + а 2 Визначник цієї системи лінійних рівнянь
є визначником Вандермонда і оскільки всі вузли інтерполяції х1, х2, …, хn різні, то він не дорівнює нулю. Тому система лінійних рівнянь (1) завжди має єдиний розв’язок. Отже, єдиний розв’язок завжди має задача інтерполювання многочленом (1). Многочлен Рn(х), який задовольняє умови Рn(хi) = yi = f (xi) (i = 0,1,…,n) називають інтерполяційним многочленом.
Інтерполяційна формула Лагранжа Хоч інтерполяційний многочлен, що задовольняє умови (1) і єдиний, проте можливі різні форми його запису. Означення 3. Многочлен Ln(x) = називається інтерполяційним многочленом Лагранжа для функції f (x). Наближену рівність f (x) ≈ Ln(х) називають інтерполяційною формулою Лагранжа. Очевидно, що Ln(хi) = f (xi) (i = 0,1,…,n), тобто що інтерполяційний многочлен Лагранжа задовольняє умови (1). Розглянемо два окремих випадки цієї інтерполяційної формули.
1. Нехай n = 1, тобто значення функції f задано в двох вузлах х0 і х1, f (х0) = у0, f (х1) = у1. Тоді інтерполяційна формула має вигляд f (x) ≈ Цю формулу називають формулою лінійного інтерполювання. Геометрично це дуга кривої у = f (x) на відрізку [x0;x1] замінюється відрізком прямої, що лежить між точками (x0;у0) і (х1;у1). 2. Нехай n = 2. Функцію f задано в трьох вузлах xі і f (xі) = уi (i = 0,1,2). У цьому разі інтерполяційна формула набирає вигляду f (x) ≈ Цю формулу називають формулою квадратичного інтерполювання. Геометрично це дуга кривої у = f (x) на відрізку [x0;x1] замінюється дугою параболи, що проходить через точки (хi; уi) (i = 0,1,2). Приклад. Побудувати інтерполяційний многочлен Лагранжатретього степеня для функції f, заданої таблицею
і знайти наближене значення функції в точці х = 2. За умовою задачі L3(х) =
Інтерполяційний многочлен Лагранжа можна записати компактніше. Для цього введемо многочлен n + 1 – го степеня виду ωn+1(х) = (x – x0)(x – x1)…(x – xn). Продиференціювавши цей добуток, дістанемо ω´n+1(х) = Теорема 1. (Оцінка похибки інтерполювання). Якщо вузли інтерполювання xi (і = 0, 1, …, n) різні і належать відрізку [a; b], функція f (x) n + 1 раз неперервно диференційовна на [a; b], то похибка інтерполювання Rn(f,x) = Доведення. Нехай z є [a; b], z ≠ хi (і = 0,1,…,n); покладемо φ(х) = f (x) – Ln(x) – Kωn+1(х), де число K обране так, щоби φ(z) = 0 (тобто K = При такому K функція φ(х) має n + 2 коренів: у точках хi (і = 0,1,…,n) та z. За теоремою Ролля між двома різними коренями φ(х) похідна φ´(х) має принаймні один корінь. Отже, φ´(х) має принаймні n + 1 різних коренів на [a; b]. Застосувавши теорему Ролля до функції φ´(х), дістанемо, що її похідна φ´´(х) має принаймні n різних коренів на [a; b]. Продовжуючи ці міркування далі, нарешті дістанемо, що φ(n+1)(х) має принаймні один корінь у деякій точці ξ = ξ (z) є [a; b]. Оскільки Ln(x) – це многочлен степеня n, ωn+1(х) – многочлен степеня n + 1, то Ln(n+1)(x) = 0, ωn+1(n+1)(х) = (n+1)!. Звідси φ(n+1)(х) = f (n+1)(x) – K(n+1)!, а тому φ(n+1)(ξ) = 0 = f (n+1)(ξ) – K(n+1)!, звідки K =
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.158.206 (0.008 с.) |


 у P(x)
у P(x)




 у3
у3
 у5 = у6
у5 = у6
 у2
у2
 у1
у1 О х1 х2 х3 х4 х5 х6
О х1 х2 х3 х4 х5 х6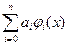 , де φi(х) – деякі фіксовані функції, коефіцієнти а i шукають з умови збіжності значень наближаємої і інтерполюючої функцій у вузлах інтерполяції: f (xj) =
, де φi(х) – деякі фіксовані функції, коефіцієнти а i шукають з умови збіжності значень наближаємої і інтерполюючої функцій у вузлах інтерполяції: f (xj) =  (j = 0,1,…,n). Найчастіше Рn – многочлен, φi(х) = хi (i = 0,1,…,n), Рn =
(j = 0,1,…,n). Найчастіше Рn – многочлен, φi(х) = хi (i = 0,1,…,n), Рn =  , а відповідна система лінійних рівнянь має вигляд:
, а відповідна система лінійних рівнянь має вигляд: а 0 + а 1х0 + а 2
а 0 + а 1х0 + а 2  +… + а n
+… + а n  = y0
= y0 +… + а n
+… + а n  = y1
= y1 +… + а n
+… + а n  = yn .
= yn .
 f (xi)
f (xi) .
. .
.
 , f (2) = L3(2) ≈ 5,67.
, f (2) = L3(2) ≈ 5,67. . Поклавши х = хi (і = 0, 1, …, n), матимемо ω´n+1(хi) = (xi – x0)(xi – x1)…(xi – xi-1)(xi – xi+1)…(x – xn). Підставивши ці вирази для ωn+1(х) і ω´n+1(хi) у інтерполяційний многочлен Лагранжа, знайдемо Ln(x) = ωn+1(х)
. Поклавши х = хi (і = 0, 1, …, n), матимемо ω´n+1(хi) = (xi – x0)(xi – x1)…(xi – xi-1)(xi – xi+1)…(x – xn). Підставивши ці вирази для ωn+1(х) і ω´n+1(хi) у інтерполяційний многочлен Лагранжа, знайдемо Ln(x) = ωn+1(х)  .
. ωn+1(х), де ξ = ξ (x) є [a; b].
ωn+1(х), де ξ = ξ (x) є [a; b]. ). Оскільки φ(z) = 0 = f (z) – Ln(z) – Kωn+1(z), то Rn(f,z) = f (z) – Ln(z) = Kωn+1(z).
). Оскільки φ(z) = 0 = f (z) – Ln(z) – Kωn+1(z), то Rn(f,z) = f (z) – Ln(z) = Kωn+1(z). . Отже, Rn(f,z) = Kωn+1(z) =
. Отже, Rn(f,z) = Kωn+1(z) = 


