
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ітераційні методи та оператор стиску.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Метод дихотомії є прикладом ітераційного методу (або ж методу послідовних наближень) розв’язування рівнянь. У цих методах завжди формують послідовність хn наближень, де кожне наступне обчислюється з попередніх за певним (рекурентним) правилом; наближення хn збігаються до точного значення кореня рівняння. Але ж найчастіше у таких методах рівняння f (x) = 0 замінюють еквівалентним х = φ(х), де φ(х) – деяка неперервна функція (φ(х) = х – f (x) наприклад). Далі обирають початкове наближення х0 і послідовно обчислюють наступні наближення: хk = φ(хk-1), k = 1,2,…. Якщо послідовність хk має границю х*, тобто Метод простої ітерації має простий геометричний зміст. Побудуємо графіки функцій y = x і y = φ(х). Абсциса точки перетину графіків цих функцій є коренем рівняння х = φ(х).
в г Рисунок 1 Довільно вибираємо точку х0 і проводимо через неї пряму, паралельну осі ординат до перетину з кривою у = φ(х) у точці А0 (х0, φ(х0)). З точки А0 проведемо пряму, паралельну осі абсцис, до перетину з прямою у = х. В результаті дістанемо точку В1 з ординатою φ(х0). Спроектувавши точку В1 на вісь Ох, знаходимо абсцису х1 = φ(х0). Аналогічно через х1 проводимо пряму, паралельну осі ординат, до перетину з кривою у = φ(х) в точці А1(х1, φ(х1)). З точки А1 проводимо пряму, паралельну осі абсцис, до перетину з прямою у = х в точці В2(х2, φ(х2))), абсциса якої х2 = φ(х1) і т.д. В результаті спільні абсциси точок А1 і В1, А2 і В2, … є послідовними наближеннями х1, х2, х3,... кореня х*. На рисунку зображено випадки: а) 0 < φ'(х) <1; б) – 1 < φ'(х) <0; в) < φ'(х) > 1; г) φ'(х) < -1. Якщо │φ'(х)│< 1, то послідовні наближення хk збігаються до кореня х*, якщо │φ'(х)│>1, то послідовні наближення віддаляються від нього. Як правило, збіжність наближень забезпечує наступна умова. Означення 1. Функція φ(х) на відрізку За теоремою Лагранжа умова Ліпшиця з константою q буде виконана для функції φ(х) на відрізку Означення 2. Нехай R – метричний простір, ρ – відстань (метрика) на цьому просторі, А – оператор, визначений на R. Оператор А називають оператором стиску, якщо існує таке додатне число q < 1, що ρ(Ах, Ах′) < q ∙ ρ(х, х′) для будь – яких х, х′ є R. Точку х є R називають нерухомою точкою оператора А, якщо Ах = х. Основою для дослідження збіжності ітераційних процесів є наступна теорема Банаха. Теорема 4 (принцип стискуючих відображень). Якщо оператор стиску А визначений на повному метричному просторі R, то в R він має єдину нерухому точку, до якої збігається ітераційний процес хk = Ахk-1 (k = 1,2,…) при будь – якій початковій точці х0 є R. Доведення. Нехай х0 – довільна точка простору R, хk = Ахk-1 (k = 1,2,…). Доведемо, що послідовність хk фундаментальна. Справді, ρ(хk+1, хk) = ρ(Aхk, Aхk-1) ≤ qρ(хk, хk-1) = ρ(Aхk-1, Aхk-2) ≤ q2ρ(хk-1, хk-2) ≤ … ≤ qkρ(х1, х0). Отже, якщо m > k, то, скориставшись правилом трикутника, маємо: ρ(хm, хk) ≤ ρ(хm, хk+1) + ρ(хk+1, хk) ≤ ρ(хm, хk+2) + ρ(хk+2, хk+1) + ρ(хk+1, хk) ≤ … ≤ ρ(хm, хm-1) + … + ρ(хk+2, хk+1) + ρ(хk+1, хk) ≤ (qm-1 + … + qk+1 + qk)ρ(х1, х0) = = Тому для як завгодно малого ε > 0 існує таке натуральне N(ε), що при m > k > N(ε) виконуватиметься нерівність ρ(хm, хk) ≤ Це означає, що послідовність хk фундаментальна. Оскільки метричний простір R повний, то існує границя Нарешті доведемо, що х* – єдина нерухома точка оператора А. Припустимо, що x і y – дві різні нерухомі точки А: Ах = х, Аy = y, ρ(х, y) ≠ 0. Але А – оператор стиску, звідки ρ(х, y) = ρ(Ах, Аy) ≤ qρ(х, y), що неможливо оскільки q < 1. Теорему доведено. Теорема 5. Нехай рівняння х = φ(х) має корінь х* і в деякому околі R = {x: │x – х*│≤ r} цього кореня функція φ(х) задовольняє умові Ліпшиця │φ(х) – φ(х′)│≤ q│x – x′│ з константою Ліпшиця q < 1. Тоді 1) y = φ(х) є стискуючим відображенням на R. 2) R – відрізок ізоляції кореня х*. 3) Ітераційний процес хk = φ(хk-1) на R збігається до х* при будь – якому початковому х0. 4) Швидкість цієї збіжності характеризується нерівністю │xk – x*│ ≤ qk│x0 – x*│. Доведення. 1) Функція φ(х) відображає відрізок R у самого себе: φ(R) 2) Тому з принципу стискуючих відображень випливає, що на R існує одна і тільки одна нерухома точка відображення y = φ(х) і за умовою це x*, випливає також і 3). 4) З умови Ліпшиця маємо: │xk – x*│ = │φ(хk-1) – φ(х*)│ ≤ q│xk-1 – x*│ = q│φ(хk-2) – φ(х*)│ ≤ q2│xk-2 – x*│ ≤ … ≤ qk│x0 – x*│. Теорему доведено. Отже, послідовність xk збігається до х* принаймні із швидкістю геометричної прогресії із знаменником q: чим менше q, тим збіг швидше.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 479; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.104.30 (0.007 с.) |

 = х*, то ця границя буде розв’язком рівняння х = φ(х). Справді, х* =
= х*, то ця границя буде розв’язком рівняння х = φ(х). Справді, х* =  хk =
хk = 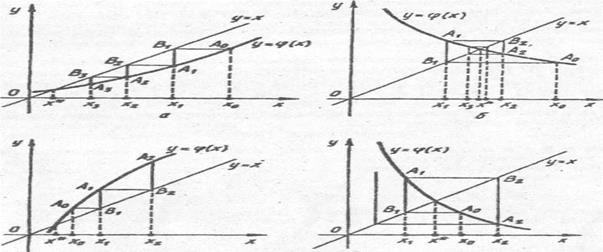
 задовольняє умові Ліпшиця, якщо для будь – яких точок х, х′ є
задовольняє умові Ліпшиця, якщо для будь – яких точок х, х′ є  (х є
(х є  ρ(х1, х0) ≤
ρ(х1, х0) ≤  ρ(х1, х0).
ρ(х1, х0). R. Справді, якщо х є R, то y = φ(х) також належить R оскільки │y – x*│ = │φ(х) – φ(х*)│ ≤ q│x – x*│ ≤ r. Множина точок відрізка R є повним метричним простором з відстанню ρ(х, х′) = │x – x′│. За умовою теореми ρ(φ(х), φ(х′)) = │φ(х) – φ(х′)│ ≤ q│x – x′│ = q ∙ ρ(х, х′), 0 < q < 1. Отже відображення y = φ(х) є оператором стиску на R за означенням.
R. Справді, якщо х є R, то y = φ(х) також належить R оскільки │y – x*│ = │φ(х) – φ(х*)│ ≤ q│x – x*│ ≤ r. Множина точок відрізка R є повним метричним простором з відстанню ρ(х, х′) = │x – x′│. За умовою теореми ρ(φ(х), φ(х′)) = │φ(х) – φ(х′)│ ≤ q│x – x′│ = q ∙ ρ(х, х′), 0 < q < 1. Отже відображення y = φ(х) є оператором стиску на R за означенням.


