
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оператор квадрата момента импульсаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Собственные значения и собственные функции операторов квантовой механики. Для каждого оператора можно найти функции, которые являются его собственными функциями, т. е. удовлетворяют требованию
Это главный постулат квантовой механики. где В классической механике:
Уравнение для собственных функций и собственных значений оператора энергии будет
где Е - собственное значение оператора энергии; В явном виде.
Интегрируя это уравнение в частных производных второго порядка и выбирая те решения, которые удовлетворяют стандартным условиям, получают совокупность собственных функций оператора энергии
Средние значения физических величин.
В классической механике каждая динамическая величина имеет определённое значение. В квантовой механике дело обстоит иначе. Например, система находится в состоянии, которое является результатом суперпозиции состояний Если система находится либо в состоянии
Здесь в классической физике получилось бы одно строго определённое число. В квантовой механике получается не одно определённое число, а одно из двух чисел: или А если известны вероятности, то можно вычислить среднее значение. Среднее значение координаты х.
Если волновая функция нормирована к единице, то
Учитывая, что оператор координаты “
Аналогично
Второй постулат квантовой механики:
где Например: 1)
где
все интегралы вида функции. 2) Определим P
Как и в классической механике, 3) Вычислим средние значения кинетической и потенциальной энергии:
т. е. средняя потенциальная энергия равна средней кинетической, как и в классической механике.
И как и следовало ожидать, поскольку нулевое состояние есть состояние с определённой энергией.
Условия возможности одновременного измерения разных механических величин. Согласно одному из основных постулатов квантовой механики, механической величине можно приписывать определённое значение только в том случае, когда это значение является собственным значением При каких условиях две или несколько механических могут иметь одновременно определённые значения. Две механические величины F и G имеют определённые значения, если состояние описывается функцией Например: Собственные функции этих операторов удовлетворяют уровням.
Где Функция
удовлетворяет всем этим трем уравнениям, т.е. является общей собственной функцией операторов ТЕОРЕМА: Если операторы имеют общие собственные функции, то такие операторы коммутируют. Пусть
Следовательно, Обратная теорема: Если операторы коммутируют, то они имеют общие собственные функции. Динамические переменные
Откуда следует Аналогично Координатам соответствующая другой координате составляющая импульса также коммутируют.
Но координата и соответствующая ей составляющая импульса не коммутируют,
т.е. или Не могут иметь определенные значения координаты m соответствующие mm составляющие количества движения, либо одна из них имеет определенное значение m тогда другая будет неопределенна. Составляющие момента импульса не коммутируют:
Соотношения неопределенностей. В классической механике записаны так Т.е. на опыте, исходя на основе физических соображений, не можем одновременно получить абсолютно точные значения. Неопределенности обусловлены не совершенством наших измерений, а самой природой материи. Квантовая механика приводить к неизбежности этих неопределенностей. Неопределенности или неточности характеризуются квадратным корнем из среднего квадрата отклонения:
Они указывают верхний предел точности, который может быть достигнут при одновременном измерении координат m импульсов; произведение неточностей не может быть меньше Свободная частица. Одна частица, движущаяся в отсутствие действия сил в направлении, которое мы примем за ось X. Т.к. силы отсутствуют, то U=const мы можем принять ее равной нулю. Функция Гамильтона в классической механике состоит из одной кинетической энергии
при выбранной оси координат x:
Оператор Гамильтона:
Уравнение Шредингера
Частные решения этого уравнения, таковы Эти условия удовлетворяют стандартным условиям конечности m непрерывности во всем пространстве при любых положительных значениях E: E>0. Спектр собственных значений энергии в данном случае сплошной, в отличие от дискретного спектра.
Движение в центральном поле. Оператор момента количества движения.
Движение в поле центральных сил. Важную роль играет в квантовой механике оператор момента количества движения. В декартовых координатах:
Теперь мы должны перейти в этой главе к сферическим координатам:
Напишем полный дифференциал . Переход к сферическим координатам, пологая, что r и V остаются постоянными, а изменяется то
Аналогично выводится
Операторы Оператор квадрата момента количества движения
Каждый из операторов коммутирует с оператором
Оператор квадрата момента импульса имеет общие собственные функции с операторами каждой из его проекций. Законы сохранения в центрально симметричном поле. Оператор энергии полярных координатах:
Вводится оператор радиального момента:
Если принять во внимание, что Оператор любой составляющей момента количества движения коммутирует с
Это означает, что численное значение момента количества движения сохраняется во времени. А поэтому численное значение момента количества движения, одна из его проекций и энергия могут одновременно определенные значения.
Шаровыми функциями называются шаровые полиномы (одновременные), удовлетворяющие уравнению Лапласа
В сферических координатах
Где l есть квантовое число момента количества движения.
тогда момент количества движения
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1707; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |


 (1)
(1) - действительное число для ирмитовых операторов и называется собственным значением оператора
- действительное число для ирмитовых операторов и называется собственным значением оператора  , принадлежащим собственной функции
, принадлежащим собственной функции  .
.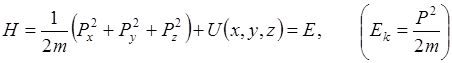

 - собственная функция.
- собственная функция.
 .
. с собственными значениями
с собственными значениями 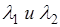 .
. , либо в состоянии
, либо в состоянии  , то соответствующее измерение даст определенное число
, то соответствующее измерение даст определенное число  или
или  соответственно. Какое значение будет получатся, когда система находится в состоянии
соответственно. Какое значение будет получатся, когда система находится в состоянии


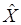 ”есть просто умножение на х:
”есть просто умножение на х:


 .- обобщённые координаты.
.- обобщённые координаты. линейного гармонического осциллятора в нормальном состоянии. Нормированная волновая функция этого состояния известна.
линейного гармонического осциллятора в нормальном состоянии. Нормированная волновая функция этого состояния известна.


 вследствие нечётности подынтегральной
вследствие нечётности подынтегральной

 в этом случае равны нулю, что и следовало ожидать из соображений симметрии функции
в этом случае равны нулю, что и следовало ожидать из соображений симметрии функции  относительно х.
относительно х.







 - собственные значения операторов.
- собственные значения операторов.
 . Это показывает, что проекции количества движения на все три оси координат могут иметь одновременно определенные значения.
. Это показывает, что проекции количества движения на все три оси координат могут иметь одновременно определенные значения. .
.


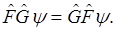










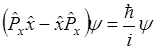




 .
. 






 , оператор импульса будет
, оператор импульса будет







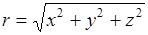





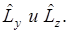
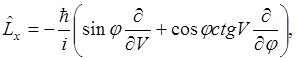




 - оператор Лежандра.
- оператор Лежандра. 

 .
.





 то
то  .
.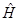 .
. .
. и
и 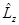 коммутируют с
коммутируют с  имеют общие собственные функции.
имеют общие собственные функции. , где У - шаровая функция.
, где У - шаровая функция.  .
. или в декартовых координатах
или в декартовых координатах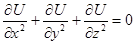


 - собственное значение квадрата момента количества движения.
- собственное значение квадрата момента количества движения. т.е.
т.е. 
 принимает собственные значения
принимает собственные значения  - собственная функция оператора.
- собственная функция оператора.


