Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение простейших задач в сферических координатах.Содержание книги
Поиск на нашем сайте
Ротатор – представляет собой частицу, движущуюся по сфере радиуса Угловая часть описывается шаровыми функциями, а для определения радиальной функции берем уравнение
где
Энергия ротатора зависит от орбитального квантового числа, магнитное квантовое число, характеризующее проекцию момента
Состояния: l= 0, 1, 2, 3, 4 … s, p, d, f, g и так далее. Рассмотрим S и P состояния ротатора. В S-состоянии
В P-состоянии
Плотности вероятности:
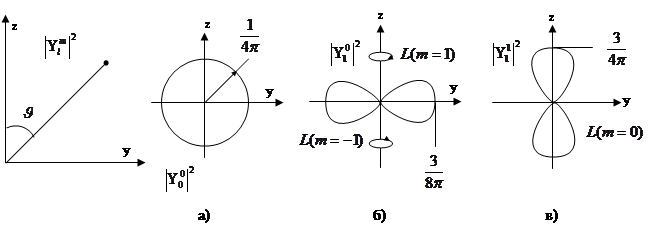
Величина Поскольку квадрат модуля Графически распределение плотности вероятности (1), (2), (3) представлены на рисунке:
Чтобы поучить полную картину нужно вращать вокруг оси Z. Рис а) и из (1) направление момента Из (2) и рис. б) следует, что наиболее вероятной из всех траекторий ротатора в P-состоянии с При l=1 и m =0 наиболее вероятной орбитой ротатора является та орбита, которая лежит в плоскости, проходящей через ось Z (рис. в)). При этом момент направлен перпендикулярно оси Z. Аналогичным образом можно исследовать состояния с l = 2 (пять значений Во всех случаях наблюдается размытость электронного облака. Существуют фотографии электронного облака для различных состояний водородоподобного атома. Правила отбора.
a) b) соответствует правому вращению c) соответствующие левому вращению Разрешенными будут только те переходы, для которых изменение квантового числа m орбитального числа l равны
это имеет место для центрально-симметричных систем и, в частности, для атома водорода. Литература.
Шпольский Э.В. «Атомные физика». т. I-II М. Наука, 1984 г. Блохинцев Д.И. «Основы Квантовой механики» М. Наука, 1983 г. Гольдин Л.Л., Новикова Г.И. «Введение в квантовую физику». М. Наука, 1988 г. Матвеев А.Н. «Атомная физика» М.Высшая школа 1989 г. Ландау Л.Д., Лифшиц Е.М. «Квантовая механика» М. Наука 1974 г. Соколов А.А., Тернов Н.М., Жуковский В.Ч. «Квантовая механика» М. Наука 1979 г. Фок В.А. «Начала квантовой механики» М Наука 1976 г. Горяга Г.И. «Конспект лекций по атомной физике». М. Наука, 1985 г. Киттель Ч. «Введение в физику твердого тела» (перевод с американского издания) М. Наука, 1978 г. Бонч-Брусевич В.Л. «Физика полупроводников» М. Наука 1977 г. Шиллинг Г. «Статистическая физика в примерах». М. МИР 1976 г. Киреев П.С. «Физика полупроводников» М. Высшая школа,1975 г.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 608; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 . Это задача – движение под действием центральных сил, когда потенциальная энергия постоянна, и можно положить равной нулю.
. Это задача – движение под действием центральных сил, когда потенциальная энергия постоянна, и можно положить равной нулю.  .
. ,
, .
.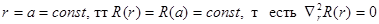 .
. - момент инерции.
- момент инерции.
 на ось Z, в выражение
на ось Z, в выражение 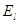 не входит. Собственному значению
не входит. Собственному значению  , зависящие от m. m может меняться от
, зависящие от m. m может меняться от 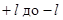 , каждому значению энергии
, каждому значению энергии 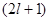 -кратно вырожденным.
-кратно вырожденным.
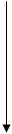 При l= 0 имеем однократно вырожденный уровень, который называется просто невырожденным.
При l= 0 имеем однократно вырожденный уровень, который называется просто невырожденным.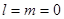 , собственная функция
, собственная функция  , соответствующая нулевому собственному значению энергии
, соответствующая нулевому собственному значению энергии  , будет равна
, будет равна 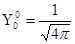 .
.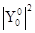 -квадрат модуля – плотность вероятности
-квадрат модуля – плотность вероятности 
 , квантовое число m может принимать три значения: -1, 0, +1, следовательно, собственному значению энергии
, квантовое число m может принимать три значения: -1, 0, +1, следовательно, собственному значению энергии  соответствуют три собственные функции:
соответствуют три собственные функции:
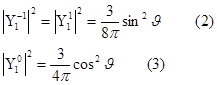
 представляет вероятность обнаружить частицу на сфере постоянного радиуса в области углов
представляет вероятность обнаружить частицу на сфере постоянного радиуса в области углов  .
.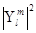 не зависит от угла
не зависит от угла  , вероятность обнаружить частицу в одном и том же интервале углов
, вероятность обнаружить частицу в одном и том же интервале углов  становится одинаковой. В силу этого произведение
становится одинаковой. В силу этого произведение  соответствует плотности вероятности обнаружить частицу между углами
соответствует плотности вероятности обнаружить частицу между углами  .
.
 , так как
, так как  . Покоящаяся же материальная точка может с равной вероятностью находиться в любом месте сферической поверхности радиуса
. Покоящаяся же материальная точка может с равной вероятностью находиться в любом месте сферической поверхности радиуса  , то есть все положения ротатора возможны и равноправны. Классического аналога S-состояние не имеет.
, то есть все положения ротатора возможны и равноправны. Классического аналога S-состояние не имеет. является та, которая расположена в плоскости (xy), причем состояния с
является та, которая расположена в плоскости (xy), причем состояния с  отличаются одно от другого направлением оси вращения: при
отличаются одно от другого направлением оси вращения: при 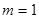 ротатор обладает правым вращением (момент количества движения
ротатор обладает правым вращением (момент количества движения 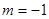 - левым (момент
- левым (момент  ), с l =3 и так далее.
), с l =3 и так далее.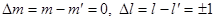 ;
; ;
;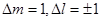 .
.