
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение Шредингера для атома водорода.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
В сферической системе координат для электрона:
n – главное квантовое число, l – побочное квантовое число, m – магнитное квантовое число. Вероятность
В состоянии s(l=0, m=0) волновая функция сферически симметрична (т.е. не зависит от углов ( Нормированные собственные
или в атомных единицах
где в качестве единицы измерения длины выбран радиус первой боровской орбиты
При таком выборе единицы длины расстояния осей ядра В s-состоянии вероятность
Момент импульса L и магнитный момент P, обусловлены орбитальным движением электрона:
где l – орбитальное квантовое число l=(0,1,2,3,…,(n-1)),
Проекция момента импульса Lz и магнитного момента Pz на направление внешнего магнитного поля:
где m – магнитное квантовое число ( Гиромагнитные отношения для орбитальных магнитного момента P и момента импульса L
Момент импульса s и магнитный момент
Проекции спиновых моментов импульса Sz и магнитного момента
Проекции Sz и Гиромагнитное отношение для спиновых магнитного и механического моментов
Распределение электронов по состояниям в атоме записывается с помощью спектроскопических символов:
Электронная конфигурация записывается следующим образом: 2p – (n =2, l =1); 2p2 – (электронов в атоме ровно 2m и т.д.) Принцип Паули: в атоме не может находиться два и более электронов, характеризуемых одинаковым набором четырех квантовых чисел: n, l, m, ms (где ms – спиновое магнитное квантовое число: Оператор Лапласа в сферических координатах:
Ze – заряд ядра. Сила, связывающая электроны с ядром на расстояниях порядка атомных размеров (
Для низшего энергетического состояния l =0 и оно полной сферической симметрией, так что функция
Обозначим
простейшее решение этого уравнения, имеющее конечное значение при r =0 и стремящееся к нулю при
Действительно, имеем, прежде всего
подставляем в выше написанное уравнение, и после сокращения на
это соотношение должно иметь место при любом r, вследствие чего оба двучлена, взятые в скобки, должны равняться нулю, каждый в отдельности, т.е.
Сравнивая с формулой Бора для бальмеровых уровней энергии мы видим, что El, есть не что иное, как первый бальмеров уровень, соответствующий главному квантовому числу n= 1, l= 0, оно символически обозначается ls. Z=1 и иногда энергия El водородного атома в нормальном состоянии, с обратным знаком, это и будет энергия ионизации атома водорода.
хорошее совпадение с экспериментальными данными. Вычислим теперь вероятность электрона в элементе объема
Постоянная Введем новую постоянную тогда: плотность вероятности W(r) обращается в нуль при получим откуда где С таким выражением встречались в теории Бора: n= 1, Z= 1
это радиус первой водородной орбиты. Азимутальное квантовое число теории Бора
и здесь состояние ls характеризуется сферической симметрией, так что распределение вероятности представляет собой сферическое «облако», а не плоский образ, соответствующий «орбите». Заряд электрона представляют на всех графиках размазанный по всему пространству в виде облака.
Уравнение Шредингера
следует решать по методу разделения переменных, полагая
Умножая исходное уравнение на
Так как слева стоит величина, зависящая только от r, справа – только от углов Для радиальной: Для угловой: Полагая ее разделяют по сферическим углам:
Частные производные заменяются полными дифференциалами.
Каждая из функций Таким образом, для определения собственных значений энергии
нормировка производится для каждой из функций по отдельности.
Частное решение для азимутальной функции: либо Волновая функция должна удовлетворять условию однозначности,
где из условия нормировки
m – магнитное квантовое число, собственные значения его известны. Решение второго уравнения:
l – орбитальное квантовое число, l = 0,1,2,3,…, n -1
квантовое число характеризует собственное значение
Сравнивая с классической функцией Гамильтона
где В классической механике момент количества движения
В случае центральных сил Чтобы обобщить классическое выражение на квантовый случай, надо заменить
тогда
действуя
m – характеризует проекцию момента количества движения на ось z.
При
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1056; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


 - собственное значение энергии электрона в атоме, n=1,2,3,…
- собственное значение энергии электрона в атоме, n=1,2,3,… -определяется тремя параметрами;
-определяется тремя параметрами; того, что электрон находится в области, ограниченной элементом объема dv1, взятого в окрестности точки с координатами
того, что электрон находится в области, ограниченной элементом объема dv1, взятого в окрестности точки с координатами 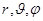 определяется
определяется (в сферических координатах).
(в сферических координатах). )).
)). -функции, отвечающие за 1s-состояние (основному) и 2s-состоянию, имеют вид:
-функции, отвечающие за 1s-состояние (основному) и 2s-состоянию, имеют вид:

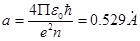
 будет выражаться в безразмерных величинах.
будет выражаться в безразмерных величинах.
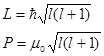


 ).
).
 , обусловлены спином электрона
, обусловлены спином электрона
 на направление внешнего магнитного поля
на направление внешнего магнитного поля

 ).
).
 см) есть кулоновская сила притяжения. Соответствующая ей потенциальная энергия
см) есть кулоновская сила притяжения. Соответствующая ей потенциальная энергия
 . Поэтому члены, содержащие производные по
. Поэтому члены, содержащие производные по  в операторе Лапласа, равны нулю и уравнение Шредингера принимает вид:
в операторе Лапласа, равны нулю и уравнение Шредингера принимает вид:

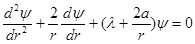
 есть
есть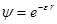



 ,
,
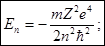

 . Обозначим через N нормирующий множитель.
. Обозначим через N нормирующий множитель. , где
, где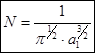
 имеет размерность см-1.
имеет размерность см-1. , связанную с
, связанную с 
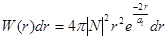
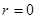 и асимптотически стремится к нулю при
и асимптотически стремится к нулю при  . Эта вероятность достигает максимума на расстоянии: продифференцируем последнее уравнение и приравняем к нулю, и после сокращения на
. Эта вероятность достигает максимума на расстоянии: продифференцируем последнее уравнение и приравняем к нулю, и после сокращения на 
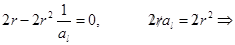
 , где
, где 
 ; находим
; находим  ;
;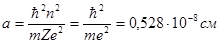 ;
;


 получаем:
получаем:
 , называемой постоянной разделения.
, называемой постоянной разделения.



 - постоянная разделения.
- постоянная разделения.

 зависит только от одной переменной.
зависит только от одной переменной.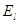 и соответствующих им собственных значений функций
и соответствующих им собственных значений функций  получим три уравнения:
получим три уравнения:



 ,
, .
. необходимо наложить условие периодичности
необходимо наложить условие периодичности  , из которого следует
, из которого следует ,
, .
.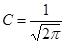



 , входящего в квантовое операторное выражение функции Гамильтона
, входящего в квантовое операторное выражение функции Гамильтона .
. ,
, , видим, что оператору
, видим, что оператору  в классическом случае соответствует квадрат момента количества движения
в классическом случае соответствует квадрат момента количества движения  , а оператору
, а оператору  - квадрат радиального импульса
- квадрат радиального импульса  .
. , а момент внешних сил
, а момент внешних сил 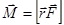 , и изменения
, и изменения 

 , тогда
, тогда  закон сохранения количества движения.
закон сохранения количества движения. оператором импульса
оператором импульса ,
, - не коммутируемые операторы.
- не коммутируемые операторы. ;
;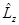 на шаровую функцию
на шаровую функцию ;
; - собственная функция операторов
- собственная функция операторов 
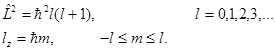
 обращается в нуль, в то время по классической теории это величина не может вообще обращаться в нуль. Состояние
обращается в нуль, в то время по классической теории это величина не может вообще обращаться в нуль. Состояние  не имеет классического аналога. Механический момент атома, находящегося в наинизшем состоянии, обращается в нуль. Экспериментальные данные из области спектроскопии подтверждают этот квантово-механический результат.
не имеет классического аналога. Механический момент атома, находящегося в наинизшем состоянии, обращается в нуль. Экспериментальные данные из области спектроскопии подтверждают этот квантово-механический результат.


