
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон Стефана-Больцмана (1884)Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Шкала электромагнитных волн
Видимый свет:
Оптическое излучение: видимое излучение, ультрафиолетовое и инфракрасное излучение.
Излучение тел происходит: a) под действием освещения тепла от внешнего источника – фотолюминесценция; b) свечение газов или паров под действием электрического разряда – электролюминесценция; c) Тепловое излучение – происходит путем нагревания тел, но оно имеет место и при низких температурах (комнатных). Последнее излучение соответствует низким длинам – инфракрасным волнам; d) Химилюминесценция – сопровождается химическими превращениями внутри тела(свечение гниющего дерева, свечение фосфора, медленно окисляющегося на воздухе).
Тепловое излучение.
Остальные излучения (свечения) за счет любого вида энергии, кроме внутренней (тепловой), называется люминесценцией. Химилюминесценция, электролюминесценция, катодолюминесценция, фотолюминесценция. Тепловое излучение происходит при любой температуре. При невысоких температурах излучаются лишь инфракрасные волны. На рис.1 излучающее тело окружили оболочкой с идеально отражающей поверхностью (r – коэффициент отражения равен 1). Происходит непрерывный обмен между телом и заполняющим оболочку излучением. Излучение равновесное – то есть распределение энергии между телом и излучением остается неизменным. Единственное тепловое излучение может находиться в равновесии с излучающим телом, это обусловлено тем, что его интенсивность возрастает при повышении температуры.
Основные характеристики: Интенсивность теплового излучения характеризуется потоком энергии, измеряемой в ваттах. Энергетическая светимость
где Как Энергетическая (или испускательная) светимость равна:
Излучение можно характеризовать вместо частоты
Продифференцируем это
Знак «-»показывает, что с возрастанием Доля энергетической светимости, приходящая на интервал
Если
то есть С помощью этой формулы можно перейти от Пусть на элементарную площадку тела падает поток лучистой энергии
Закон Кирхгоффа (1859)
Отношение испускательной способности тела к поглощательной способности тела не зависит от природы тела, есть универсальная для всех тел функция частоты и температуры. Для абсолютно черного тела
При теоретических исследованиях для характеристики спектрального состава равновесного теплового излучения, удобно пользоваться функцией частоты Обе функции связаны друг с другом
Абсолютно черных тел в природе не существует.
где T – температура стенок. Из отверстия выходит излучение, близкое по спектральному составу к излучению а. ч. т. при той же температуре. Разлагая это излучение в спектр при помощи дифракционной решетки и измеряя интенсивность различных участков спектра, можно построить график функции Кривые, относящиеся к различным значениям температуры T абсолютно черного тела. Площадь под кривой дает энергетическую светимость а. ч. т. при соответствующей температуре, которая сильно возрастает при увеличении температуры. В равновесном состоянии энергия излучения будет распределена в объеме полости с определенной плотностью
где
Полная плотность энергии
Экспериментально получили
Эта формула связывает испускательную способность а. ч. т. с равновесной плотностью энергии. Max испускательной способности а. ч. т. с увеличением температуры смещается в сторону более коротких волн
Формула Планка (1900) Для устранения этой катастрофы Планк выдвинул гипотезу: Атомные осцилляторы излучают энергию только определенными порциями – квантами. Он нашел вид функции
Закон определяет энергию, приходящую на фотоны с частотами от
g- число возможных проекций спина на направление внешнего поля
Для электрона Число возможных проекций спина на заданное направление Из формулы Планка выводится все другие законы теплового излучения.
Закон смещения Вина
При этих
Закон излучения Вина В предельном случае
Закон Стефана-Больцмана Интегрируя формулу Планка
По всем частотам, находим полную энергию излучения, содержащуюся в объеме V=1 м3
Мощность, излучаемая в единичный телесный угол в направлении нормали к 1 м2 черной излучающей поверхности в полосе частот от
Мощность излучения Испускаемая с 1 м2 излучающей поверхности в полупространство, для случая n0 =1, определяется законом излучения Стефана-Больцмана;
Закон Релея-Джинса В предельном случае
Аналогично
Второй постулат квантовой механики:
где Например: 1)
где
все интегралы вида функции. 2) Определим P
Как и в классической механике, 3) Вычислим средние значения кинетической и потенциальной энергии:
т. е. средняя потенциальная энергия равна средней кинетической, как и в классической механике.
И как и следовало ожидать, поскольку нулевое состояние есть состояние с определённой энергией.
Условия возможности одновременного измерения разных механических величин. Согласно одному из основных постулатов квантовой механики, механической величине можно приписывать определённое значение только в том случае, когда это значение является собственным значением При каких условиях две или несколько механических могут иметь одновременно определённые значения. Две механические величины F и G имеют определённые значения, если состояние описывается функцией Например: Собственные функции этих операторов удовлетворяют уровням.
Где Функция
удовлетворяет всем этим трем уравнениям, т.е. является общей собственной функцией операторов ТЕОРЕМА: Если операторы имеют общие собственные функции, то такие операторы коммутируют. Пусть
Следовательно, Обратная теорема: Если операторы коммутируют, то они имеют общие собственные функции. Динамические переменные
Откуда следует Аналогично Координатам соответствующая другой координате составляющая импульса также коммутируют.
Но координата и соответствующая ей составляющая импульса не коммутируют,
т.е. или Не могут иметь определенные значения координаты m соответствующие mm составляющие количества движения, либо одна из них имеет определенное значение m тогда другая будет неопределенна. Составляющие момента импульса не коммутируют:
Соотношения неопределенностей. В классической механике записаны так Т.е. на опыте, исходя на основе физических соображений, не можем одновременно получить абсолютно точные значения. Неопределенности обусловлены не совершенством наших измерений, а самой природой материи. Квантовая механика приводить к неизбежности этих неопределенностей. Неопределенности или неточности характеризуются квадратным корнем из среднего квадрата отклонения:
Они указывают верхний предел точности, который может быть достигнут при одновременном измерении координат m импульсов; произведение неточностей не может быть меньше Свободная частица. Одна частица, движущаяся в отсутствие действия сил в направлении, которое мы примем за ось X. Т.к. силы отсутствуют, то U=const мы можем принять ее равной нулю. Функция Гамильтона в классической механике состоит из одной кинетической энергии
при выбранной оси координат x:
Оператор Гамильтона:
Уравнение Шредингера
Частные решения этого уравнения, таковы Эти условия удовлетворяют стандартным условиям конечности m непрерывности во всем пространстве при любых положительных значениях E: E>0. Спектр собственных значений энергии в данном случае сплошной, в отличие от дискретного спектра.
Движение в центральном поле. Оператор момента количества движения.
Движение в поле центральных сил. Важную роль играет в квантовой механике оператор момента количества движения. В декартовых координатах:
Теперь мы должны перейти в этой главе к сферическим координатам:
Напишем полный дифференциал . Переход к сферическим координатам, пологая, что r и V остаются постоянными, а изменяется то
Аналогично выводится
Операторы Оператор квадрата момента количества движения
Каждый из операторов коммутирует с оператором
Оператор квадрата момента импульса имеет общие собственные функции с операторами каждой из его проекций. Законы сохранения в центрально симметричном поле. Оператор энергии полярных координатах:
Вводится оператор радиального момента:
Если принять во внимание, что Оператор любой составляющей момента количества движения коммутирует с
Это означает, что численное значение момента количества движения сохраняется во времени. А поэтому численное значение момента количества движения, одна из его проекций и энергия могут одновременно определенные значения.
Шаровыми функциями называются шаровые полиномы (одновременные), удовлетворяющие уравнению Лапласа
В сферических координатах
Где l есть квантовое число момента количества движения.
тогда момент количества движения
Уравнение Шредингера
следует решать по методу разделения переменных, полагая
Умножая исходное уравнение на
Так как слева стоит величина, зависящая только от r, справа – только от углов Для радиальной: Для угловой: Полагая ее разделяют по сферическим углам:
Частные производные заменяются полными дифференциалами.
Каждая из функций Таким образом, для определения собственных значений энергии
нормировка производится для каждой из функций по отдельности.
Частное решение для азимутальной функции: либо Волновая функция должна удовлетворять условию однозначности,
где из условия нормировки
m – магнитное квантовое число, собственные значения его известны. Решение второго уравнения:
l – орбитальное квантовое число, l = 0,1,2,3,…, n -1
квантовое число характеризует собственное значение
Сравнивая с классической функцией Гамильтона
где В классической механике момент количества движения
В случае центральных сил Чтобы обобщить классическое выражение на квантовый случай, надо заменить
тогда
действуя
m – характеризует проекцию момента количества движения на ось z.
При
Литература.
Шпольский Э.В. «Атомные физика». т. I-II М. Наука, 1984 г. Блохинцев Д.И. «Основы Квантовой механики» М. Наука, 1983 г. Гольдин Л.Л., Новикова Г.И. «Введение в квантовую физику». М. Наука, 1988 г. Матвеев А.Н. «Атомная физика» М.Высшая школа 1989 г. Ландау Л.Д., Лифшиц Е.М. «Квантовая механика» М. Наука 1974 г. Соколов А.А., Тернов Н.М., Жуковский В.Ч. «Квантовая механика» М. Наука 1979 г. Фок В.А. «Начала квантовой механики» М Наука 1976 г. Горяга Г.И. «Конспект лекций по атомной физике». М. Наука, 1985 г. Киттель Ч. «Введение в физику твердого тела» (перевод с американского издания) М. Наука, 1978 г. Бонч-Брусевич В.Л. «Физика полупроводников» М. Наука 1977 г. Шиллинг Г. «Статистическая физика в примерах». М. МИР 1976 г. Киреев П.С. «Физика полупроводников» М. Высшая школа,1975 г. Шкала электромагнитных волн
Видимый свет:
Оптическое излучение: видимое излучение, ультрафиолетовое и инфракрасное излучение.
Излучение тел происходит: a) под действием освещения тепла от внешнего источника – фотолюминесценция; b) свечение газов или паров под действием электрического разряда – электролюминесценция; c) Тепловое излучение – происходит путем нагревания тел, но оно имеет место и при низких температурах (комнатных). Последнее излучение соответствует низким длинам – инфракрасным волнам; d) Химилюминесценция – сопровождается химическими превращениями внутри тела(свечение гниющего дерева, свечение фосфора, медленно окисляющегося на воздухе).
Тепловое излучение.
Остальные излучения (свечения) за счет любого вида энергии, кроме внутренней (тепловой), называется люминесценцией. Химилюминесценция, электролюминесценция, катодолюминесценция, фотолюминесценция. Тепловое излучение происходит при любой температуре. При невысоких температурах излучаются лишь инфракрасные волны. На рис.1 излучающее тело окружили оболочкой с идеально отражающей поверхностью (r – коэффициент отражения равен 1). Происходит непрерывный обмен между телом и заполняющим оболочку излучением. Излучение равновесное – то есть распределение энергии между телом и излучением остается неизменным. Единственное тепловое излучение может находиться в равновесии с излучающим телом, это обусловлено тем, что его интенсивность возрастает при повышении температуры.
Основные характеристики: Интенсивность теплового излучения характеризуется потоком энергии, измеряемой в ваттах. Энергетическая светимость
где Как Энергетическая (или испускательная) светимость равна:
Излучение можно характеризовать вместо частоты
Продифференцируем это
Знак «-»показывает, что с возрастанием Доля энергетической светимости, приходящая на интервал
Если
то есть С помощью этой формулы можно перейти от Пусть на элементарную площадку тела падает поток лучистой энергии
Закон Кирхгоффа (1859)
Отношение испускательной способности тела к поглощательной способности тела не зависит от природы тела, есть универсальная для всех тел функция частоты и температуры. Для абсолютно черного тела
При теоретических исследованиях для характеристики спектрального состава равновесного теплового излучения, удобно пользоваться функцией частоты Обе функции связаны друг с другом
Абсолютно черных тел в природе не существует.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 435; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.25.125 (0.011 с.) |

 Радиоволны, УКВ
Радиоволны, УКВ
 -лучи
-лучи
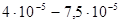 м или 0.75 – 0.4 мкм.
м или 0.75 – 0.4 мкм.







 Это испускание электромагнитных волн за счет внутренней энергии тел.
Это испускание электромагнитных волн за счет внутренней энергии тел. - поток энергии, испускаемой единицей поверхности в интервале частот
- поток энергии, испускаемой единицей поверхности в интервале частот  .
.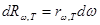
 - испускательная способность тела, функция частоты температуры тела.
- испускательная способность тела, функция частоты температуры тела. зависят от температуры.
зависят от температуры.
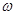 длиной волны
длиной волны  . Участку
. Участку  .
. , так как
, так как 



 ,
, ;
; 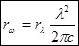
 к
к 
 , где
, где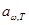 - поглощательная способность тела, безразмерная величина.
- поглощательная способность тела, безразмерная величина. - поглощенная телом часть этого потока
- поглощенная телом часть этого потока
 - серое тело,
- серое тело, - абсолютно чёрное тело.
- абсолютно чёрное тело.

 - универсальная функция Кирхгоффа есть не что иное, как испускательная способность абсолютно черного тела.
- универсальная функция Кирхгоффа есть не что иное, как испускательная способность абсолютно черного тела.

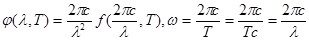

 Малое отверстие в полости близко по своим характеристикам к а. ч. т. Практически все излучение частицы поглощается в полости по закону Кирхгоффа
Малое отверстие в полости близко по своим характеристикам к а. ч. т. Практически все излучение частицы поглощается в полости по закону Кирхгоффа
 .
. Спектральное распределение этой энергии характеризуется функцией
Спектральное распределение этой энергии характеризуется функцией  , определенной условием
, определенной условием ,
, - доля плотности энергии приходящаяся на интервал частот
- доля плотности энергии приходящаяся на интервал частот  равна:
равна: 

 . С классической точки зрения на излучение были получены законы в поисках
. С классической точки зрения на излучение были получены законы в поисках 
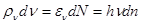 , где
, где  - энергия кванта излучения. Для света квант излучения Эйнштейном был назван фотоном.
- энергия кванта излучения. Для света квант излучения Эйнштейном был назван фотоном. - энергия фотона
- энергия фотона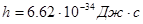 - постоянная Планка
- постоянная Планка - число фотонов излучения
- число фотонов излучения

 до
до  , для излучения в объеме
, для излучения в объеме 
 - спектральная плотность энергии
- спектральная плотность энергии , где
, где 

 , тогда для электрона
, тогда для электрона  .
. ;
; 
 плотность получения максимальна.
плотность получения максимальна.




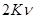 . Спектральная плотность энергии и спектральная плотность потока энергии связаны отношением
. Спектральная плотность энергии и спектральная плотность потока энергии связаны отношением ; где n0 – показатель преломления
; где n0 – показатель преломления




 .- обобщённые координаты.
.- обобщённые координаты. линейного гармонического осциллятора в нормальном состоянии. Нормированная волновая функция этого состояния известна.
линейного гармонического осциллятора в нормальном состоянии. Нормированная волновая функция этого состояния известна.


 вследствие нечётности подынтегральной
вследствие нечётности подынтегральной

 в этом случае равны нулю, что и следовало ожидать из соображений симметрии функции
в этом случае равны нулю, что и следовало ожидать из соображений симметрии функции  относительно х.
относительно х.

 - функции, описывающей состояние, в котором находится система.
- функции, описывающей состояние, в котором находится система.





 - собственные значения операторов.
- собственные значения операторов.
 . Это показывает, что проекции количества движения на все три оси координат могут иметь одновременно определенные значения.
. Это показывает, что проекции количества движения на все три оси координат могут иметь одновременно определенные значения. .
.


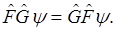










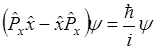




 .
. 






 , оператор импульса будет
, оператор импульса будет







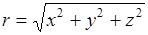





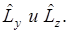
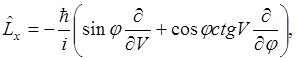




 - оператор Лежандра.
- оператор Лежандра. 

 .
.





 то
то  .
. .
. .
. и
и 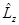 коммутируют с
коммутируют с  имеют общие собственные функции.
имеют общие собственные функции. , где У - шаровая функция.
, где У - шаровая функция.  .
. или в декартовых координатах
или в декартовых координатах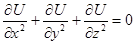


 - собственное значение квадрата момента количества движения.
- собственное значение квадрата момента количества движения. т.е.
т.е. 
 принимает собственные значения
принимает собственные значения  - собственная функция оператора.
- собственная функция оператора.

 получаем:
получаем:
 , это равенство может иметь место только в том случае, когда и левая, и правая части равны по отдельности некоторой величине
, это равенство может иметь место только в том случае, когда и левая, и правая части равны по отдельности некоторой величине 



 - постоянная разделения.
- постоянная разделения.

 зависит только от одной переменной.
зависит только от одной переменной.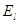 и соответствующих им собственных значений функций
и соответствующих им собственных значений функций  получим три уравнения:
получим три уравнения:



 ,
, .
. необходимо наложить условие периодичности
необходимо наложить условие периодичности  , из которого следует
, из которого следует ,
, .
.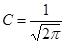



 , входящего в квантовое операторное выражение функции Гамильтона
, входящего в квантовое операторное выражение функции Гамильтона .
. ,
, , видим, что оператору
, видим, что оператору  в классическом случае соответствует квадрат момента количества движения
в классическом случае соответствует квадрат момента количества движения  , а оператору
, а оператору  - квадрат радиального импульса
- квадрат радиального импульса  .
. , а момент внешних сил
, а момент внешних сил 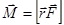 , и изменения
, и изменения 

 , тогда
, тогда  закон сохранения количества движения.
закон сохранения количества движения. оператором импульса
оператором импульса ,
, - не коммутируемые операторы.
- не коммутируемые операторы. ;
; ;
; - собственная функция операторов
- собственная функция операторов 
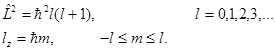
 обращается в нуль, в то время по классической теории это величина не может вообще обращаться в нуль. Состояние
обращается в нуль, в то время по классической теории это величина не может вообще обращаться в нуль. Состояние  не имеет классического аналога. Механический момент атома, находящегося в наинизшем состоянии, обращается в нуль. Экспериментальные данные из области спектроскопии подтверждают этот квантово-механический результат.
не имеет классического аналога. Механический момент атома, находящегося в наинизшем состоянии, обращается в нуль. Экспериментальные данные из области спектроскопии подтверждают этот квантово-механический результат.


